固体微电子学与半导体物理学

前言

学生赞叹于自然科学的神奇与瑰丽，震撼于科学前辈的艰苦与努力。

特设此专栏记录自己近两年的求学生活，分享自己在学习自然科学中激起的联想和感悟。

（本系列同时会穿插集成电路、半导体器件和光电子器件内容）

---

一、晶体

1.1 晶体在微米量级长程有序

晶体是原子有序排列而成的，从微观角度讲，有序排列的尺度是：微米

晶体破碎后的碎片拥有规则的几何外形是由于晶体有：自限性

晶体用腐蚀剂腐蚀会出现特定的腐蚀坑是由于：晶体内部排列有序

晶体特性：

1. 固定熔沸点（本质源于晶体内部是长程有序的）

2. 自限性（自发呈现规则的几何外形）

3. 各向异性（长程有序导致各向异性）

1.2 布拉菲格子、空间点阵

定义：X光衍射证实，晶体外形的对称性是其组成原子在空间做有规律的周期性排列的结果。把晶

体中按周期重复排列的一部分原子抽象成一个几何点，表示忽略重复周期中包含具体结构单元内

容，而集中反映周期重复的方式，这个从晶体结构中抽象出来的几何点的集合称为晶体点阵。

晶体结构=空间点阵+基元（基元内容：原子、分子、原子团、分子团等）

案例：

 1.3 结晶学原包

结晶学原胞即“晶胞”，或者叫晶体学原胞/单胞。晶胞是在实际的晶体结构中划分的，展现出实际

晶体的所有原子，不仅考虑晶体的周期性还有其对称性，因此结晶学原胞依托于14种布拉菲格子。

1.4 物理学原胞

物理物理学原胞即是所谓的“原胞”，要求每个原胞只包含一个格点。

所有具有简立方结构晶体，如CsCl晶体、钙钛矿(CaTiO3)的固体物理学原胞

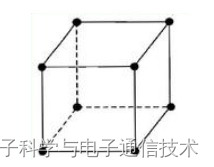
所有具有面心立方结构的晶体，其物理学原胞都是由图中基矢a1, a2, a3划分成的平行六面体

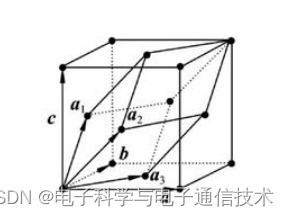
 1.5 维格纳-赛斯晶胞

维格纳-赛兹原胞，应当是取某一格点为原点，取这一格点与其他格点连线的垂直平分面所围成的空间称为维格纳-赛斯原胞。

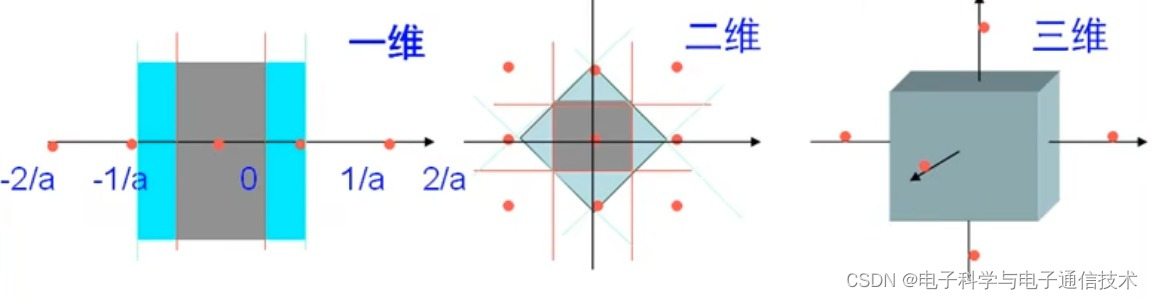
例如：体心立方的维格纳-赛兹原胞就取了最近临和次近邻的格点的垂直平分面所围成的空间为体心立方的维格纳-赛斯原胞。

---

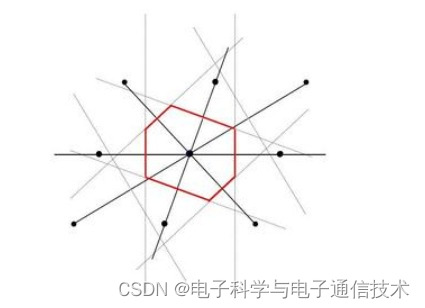
至此，基本且重要的晶体知识介绍完毕。

接下来，我们将用数学的阶梯攀登物理殿堂的高楼大厦。

---

二、能带

2.1 薛定谔方程求解电子波函数

质量为m的电子被无限高的势垒限制在长度为L的直线上

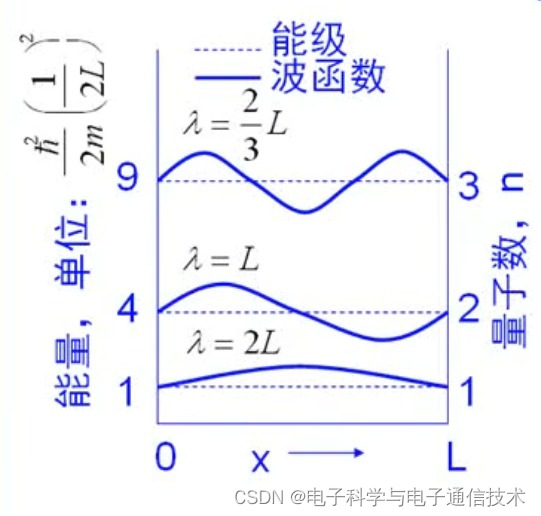
引入薛定谔方程：

电子的波函数是方程的解。波函数是一个概率函数，反应的是电子的分布和在某一点出现的概率

边界条件：电子不可逾越无限高的势垒，在边界处的电子波函数为0

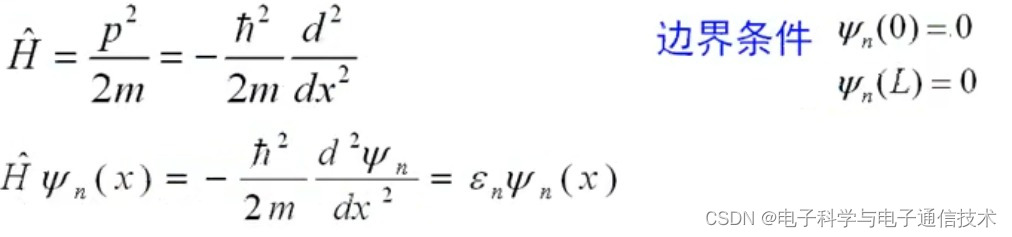
 求得解

2.2 自由电子模型

以一维点阵常数为a的线性固体为例。在计算自由电子模型时必须要考虑周期性势场，电子波在周

期性晶格中会发生布拉格衍射。

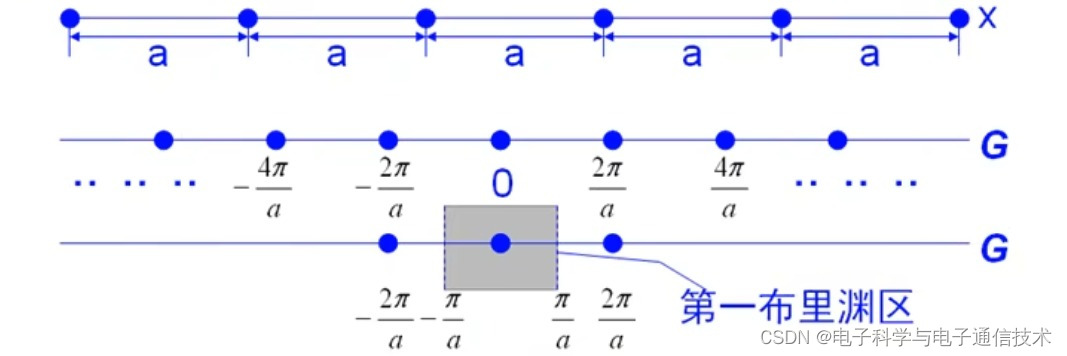
X表示时空间，G表示倒空间。布里渊区边界的波矢满足布拉格衍射条件。当电子波矢为±Π/a时，

描述电子波函数不再是行波而是驻波（布拉格衍射的结果）

两种形式的驻波，由左右两个等量的行波构成

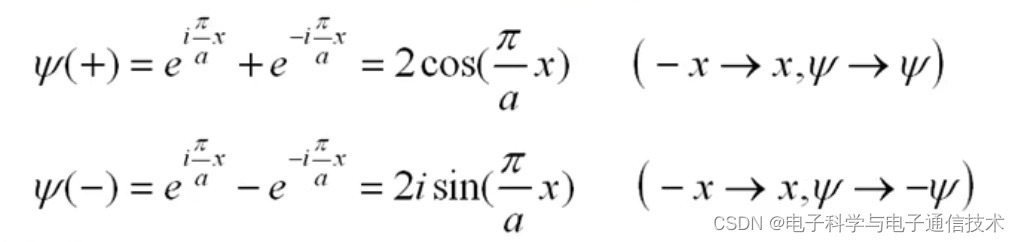
 两个驻波，使电子聚集在不同的空间区域；考虑到离子实的排列，这两个波将具有不同势能。

2.3 能隙

对于纯粹的行波，自由电子的波函数是一个恒定量。对于平面波的线性组合，近自由电子电荷密度将不再是恒量，而是具有周期性的函数

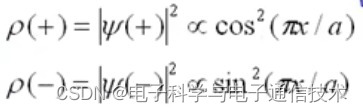
 ρ（）表示电荷几率在空间位置的分布函数。由上述公式可以看到，左右的两个行波的峰值出现在不同位置

 上图是晶格周期性势场势能的分布函数。其中黄色部分曲线与1/r成比例，r是电子与离子实的距离，电子带负电势能小于0.

引入电子波函数。纵坐标表示电子的几率密度ρ（）

------表示ρ（-）

——表示ρ（+）

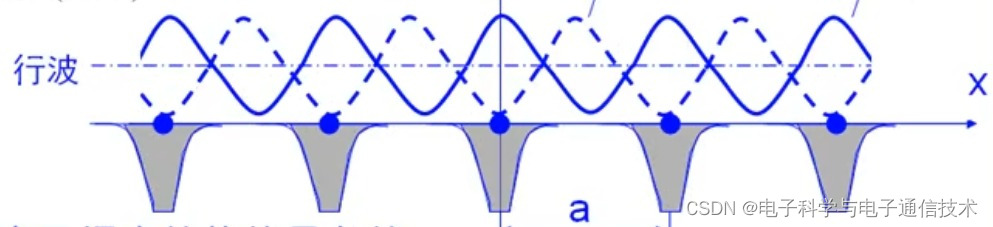
上图可以看出体系的势能具体有如下关系：U（-）＞U（行波）＞U（+）

若我们把U（+）与U（-）的能量差值用Eg表示，则两个带隙宽度就是Eg——这就是带隙。

行波在靠近布里渊区边界时波的反射比较强烈，这时边界波矢对应的能量将不再按照抛物线的形式

增长，而是以较为平缓的方式增长。在边界处的一阶微分的结果为0

2.4 布洛赫函数和克朗尼格--朋奈模型

布洛赫函数：

在周期性势场中，电子的波函数具有如下的特性：

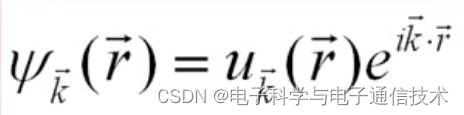
是以晶格的原胞为周期的周期函数：

 

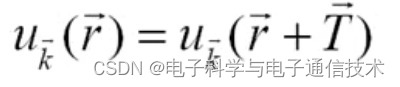
 ——函数u（）依赖于波矢k

——布洛赫函数可由行波组成，叠加后成为波包，从而表示离子实在势场中自由传播的电子

——电子具有准动量：p=ћk（此为约化普朗克常量）

克朗尼格-朋克模型：

一维周期性阱势场，纵坐标是势能，横坐标是波矢，E是本征能量。势垒是指数衰减函数，行波无势场

 根据能量守恒，在薛定谔方程中引入势能项：

 列出方程组

 

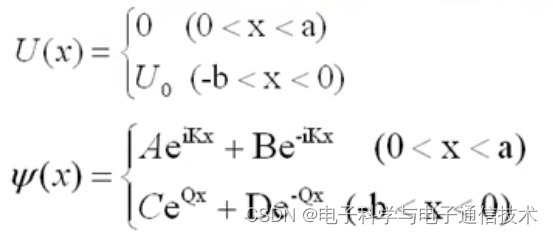
约化后求解可得（约化方式：取b=0，U=∞，即表示一个无限高的势垒）

值域（-1，1）

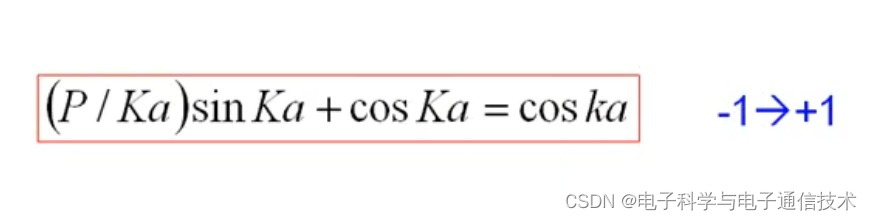
 在上述公式中：k表示波矢，K表示与能量相关的量。

根据等量关系可得到如上图

考虑周期性，可以得到如上图。

---

本章从固体电子学切入，从数学角度定性和定量揭示了能带、能隙的形成原因。由于篇幅有限，有些概念解释的不是很透彻，读者可以参考相关课本文献进行进一步学习，本文只是起到引导和发散学习的作用。如发现错误，感谢您的阅读和指正。

（由于学业繁重，本栏将不定期更新）

---