固体微电子学与半导体物理学（四）

---

写这篇文章的时候已经是四月中旬了，校园里满是春天的躁动洋溢着青春和活力。同龄人精彩的大学生活着实令我羡慕。我也想出去走走看看，但不是今年，也不是今天，更不是现在。

减少外出，多读点书；低头赶路，道心稳固。

---

五、半导体载流子的输运

---

五、半导体载流子的输运

5.1 载流子的漂移运动

5.2 载流子的散射

5.2.1 电离杂质散射

 5.2.2 晶格振动散射（声子散射）

5.2.3 等同的能谷间散射

5.3 迁移率与杂质浓度和温度的关系

5.4 强电场下的输运和负微分电导

---

5.1 载流子的漂移运动

电流密度：J

电导率：ρ

电子迁移率：μ

J=σE

σ = nq μ

半导体内有两种载流子：

5.2 载流子的散射

散射几率 P：单位时间内受到散射的次数

N（t）：在 t 时刻所有未受到散射的电子数

τ：平均自由时间（驰豫时间）

各向异性n型半导体的电导率*

以硅为例，硅的能带极值有6个，等能面为旋转椭球面。每个椭球对应的体浓度是6/n，因为沿不同

不同的方向有效质量不同，所以电子的迁移率也不同（电场方向沿x轴）

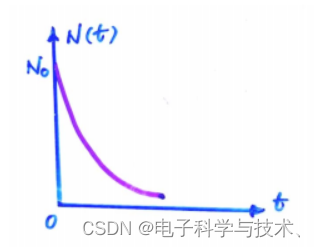
——mc*：电子电导有效质量 

——电子的电导有效质量小于空穴电导有效质量，因此电子迁移率大于空穴迁移率（2倍关系）

——1 2是纵有效质量（长轴） 3-6是横有效质量（圆面半径）

散射的根本原因：周期势场被破坏（晶体偏离理想）

载流子的散射是布洛赫震荡难以发生的原因

5.2.1 电离杂质散射

库仑力作用，属于弹性散射

1） Ni 越大，散射几率越大

2）T 越高，载流子平均热运动速度越大，散射几率越小

3）掺杂浓度越大，电离杂质数越多，散射中心越多，散射几率越大

4）温度升高。载流子运动速度增加，散射几率下降

 5.2.2 晶格振动散射（声子散射）

晶格振动类似于谐振子（弹性链）

 ——无论是声学波还是光学波，都对应频率不同的一纵两横三种波

——声学波代表质心运动，质量大，低频能量小。长声学波是弹性波，即声波

——光学波代表原子相对振动，质量小，高频能量大

——声子具有能量和动量，是一种准粒子（wq）

在坐标图的最左侧表示的就是长波，此区间长光学波为常数，长声学波为波数正比例函数。

5.2.3 等同的能谷间散射

1）对于具有单能谷的半导体，起作用的是长波，就是波长比原子间隔大很多倍的格波。

2）在长声学波中，只有纵波起主要作用

3）对于多能谷半导体。电子可以从一个极值附近散射到另一极值附近

【100】→【-100】和【100】→【010】都是允许的。区别是能量变化

4）电子在一个能谷内发生散射时，电子只与长波声子发生作用，波矢k的变化很小，能量改变很小，视为弹性散射。电子与光学波散射时，能量变化较大，散射是非弹性的。

5）电子在谷间发生散射时，有不同的情况。电子准动量发生很大改变，可以吸收或发射一个能量较高的短波声子，散射也是非弹性的

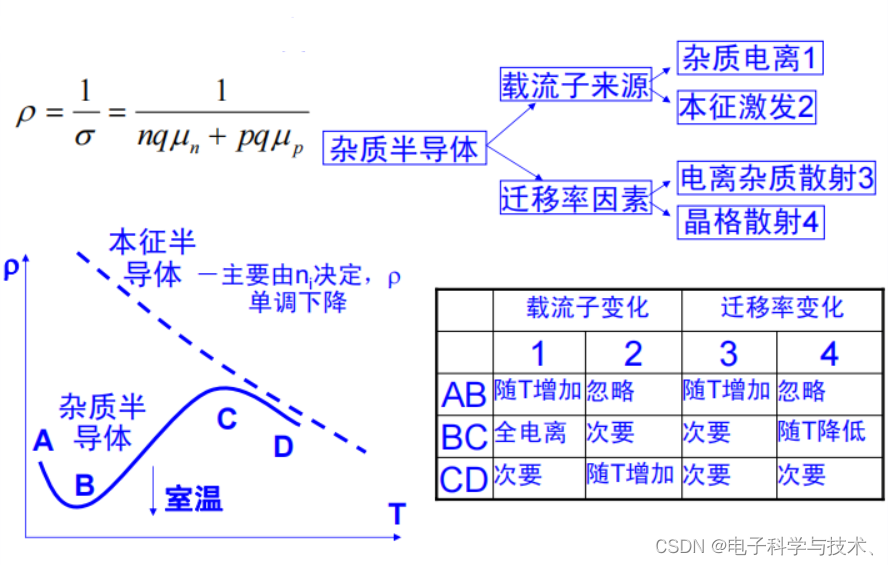
5.3 迁移率与杂质浓度和温度的关系

μ i：电离杂质散射

μs：声学波散射

两种散射可以看作是相互独立的事件，概率可以叠加。

室温：

在轻掺杂区域（参杂浓度小于10^18次方）：掺杂浓度的变化对迁移率的影响并不明显；

在重掺杂区域，随着掺杂浓度不断提高，迁移率减小；

在简并区域，掺杂浓度对迁移率的影响又不明显，曲线变化平缓。

其中多子大于少子迁移率可以认为：重掺杂时杂质能级扩展为能带所导致禁带变窄。

 上表最好背过↑

*电阻率决定于载流子浓度和迁移率*

硅，锗，砷化镓在室温下整体上都是随掺杂浓度升高，电阻率呈线性下降！在重掺杂区域，由于杂

质不能完全电离，导致偏离线性。

5.4 强电场下的输运和负微分电导

弱场下遵循欧姆定律  J=σE。电导率是个常数决定于载流子浓度和迁移率

强场下，载流子的迁移率发生变化，平均漂移速度与电场强度不成正比。

平均漂移速度Vd的饱和速度（VT）大约是10^7cm/s

强场下，发射光学声子成为动量驰豫和能量驰豫的主要机制速度可以饱和

热载流子：强场下载流子的平均动能明显高于热平衡时的值

1. 热载流子受电离杂质散射弱，但声子散射（特别是光学声子）可以很强

2.  热载流子可以在等价或不等价能谷间转移.

负微分电导

导带最低能谷1和价带极值均位于布里渊区中心k = 0处。在[111]方向布里渊区边界处还有一个极值约高出0.29eV的能谷2。当温度不太高、电场不太强时，导带电子大部分位于能谷1。

、

当电场达到3×10^3V/cm后，能谷1中的电子可从电场中获得足够的能量而开始转移到能谷2中，发生能谷间的散射，电子的准动量有较大的改变，伴随散射就发射或吸收一个光学声子

能谷2的曲率比能谷1小（曲率小，曲率半径大，有效质量大）所以，能谷2的电子有效质量较大(m”=0.067mg，mi=0.55mg)。

由于能谷2有效质量大，所以两能谷中电子迁移率不同

〔 μ1=6000 ~8000cm² /(V·s),μ2= 920cm²/(V·s)]，因纯度而异。

红色区域就是负微分电导区（迁移率为负值）。进入能谷2的电子，有效质量增加，迁移率降低，平均漂移速度减小，电导率下降，产生负阻效应

---

半导体物理基础部分分享已经接近尾声。接下来的几章将是整个半导体物理的核心部分的介绍。

文章措辞失误和论述错误在所难免，欢迎您的指正！

---