学习金半接触，就相当于正式开启了半导体器件的学习。之前的很多分析方法在本章仍然适用。
Ws：半导体功函数：费米能级到真空能级的能量差
χ：电子亲和能：导带顶到真空能级所需要能量
Wm：金属功函数
Vm：金属电势
Vs' ：半导体电势
Vs：表面势，半导体表面和体内电势差
Vms：接触电势差
En：导带底距离半导体费米能级距离
E0：真空能级，真空中静止电子的能量
Efm：金属费米能级
Efs：半导体费米能级
qφns：金属一侧的势垒高度（肖特基势垒）
qφ0：半导体表面能级，钉扎在1/3倍的Eg的地方，是一个能态海洋，表面费米能级稳定在此。
（在此时，qφns=2/3倍的Eg，qVD也高表面态密度被钉扎）
八、金半接触
8.1 金半接触能带
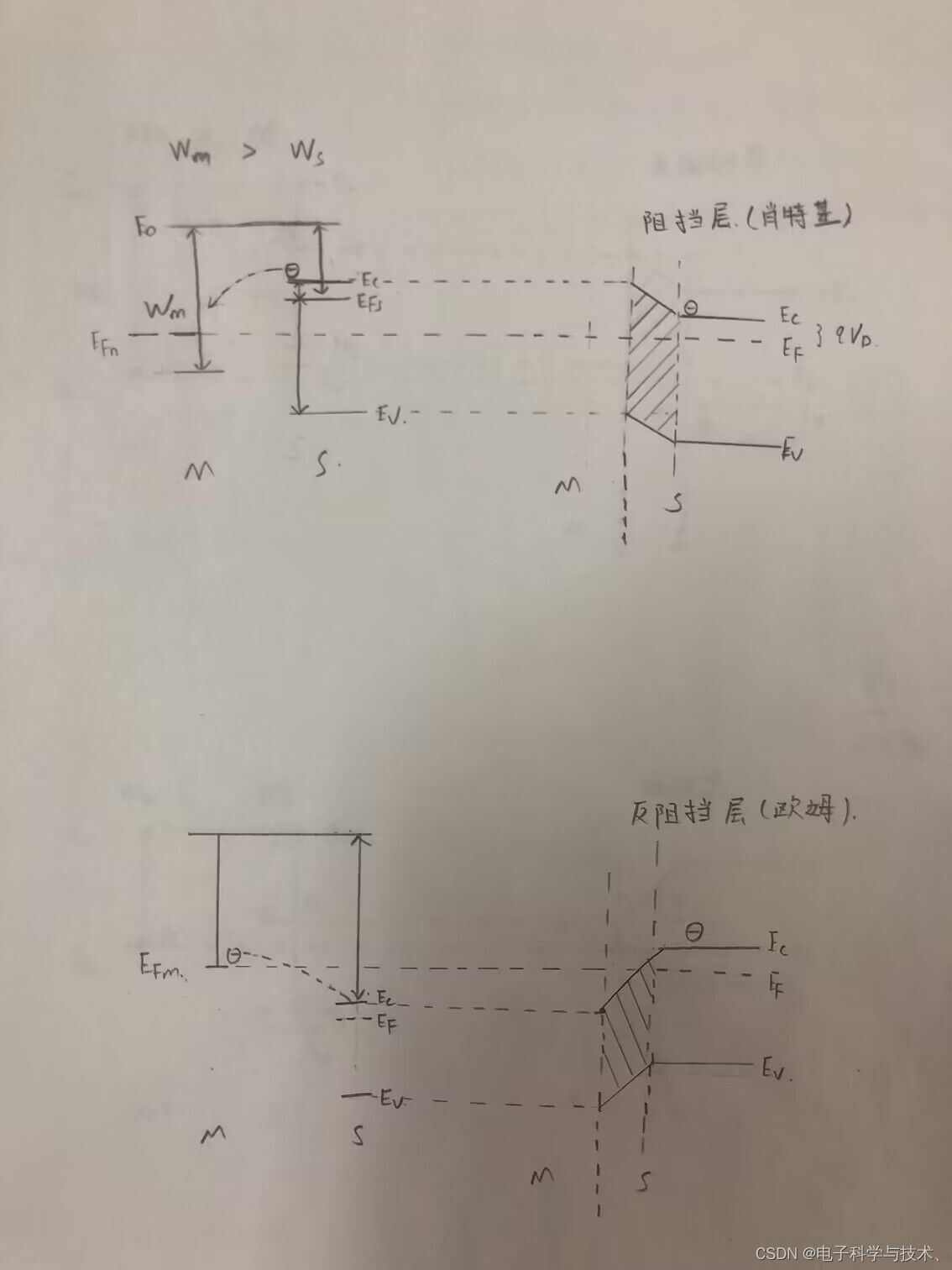
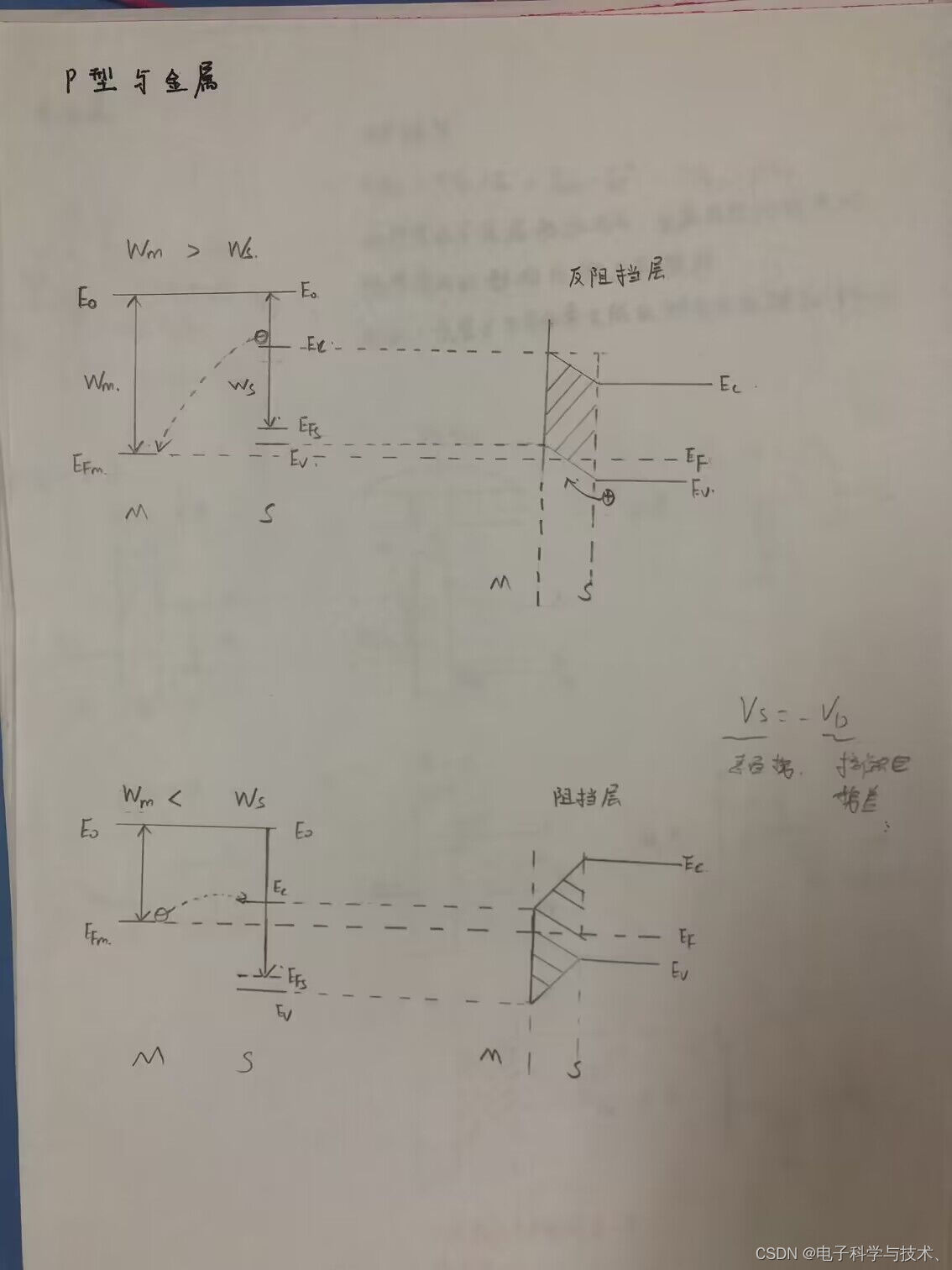
a. 接触前能带
b. qVm=Ws-Wm（Vms＜0）由于电子从半导体内转向金属一侧，所以半导体体内的电势高。金属
内的电势较低。由于间隔距离很长电势降落在很长的距离内。均匀dv里矢量连续，能带不弯曲。
c. qVm+qVs=Ws-Wm 当距离当距离很小时，电位移矢量连续，电势降落在很窄的区域电场强度很
大，因此能带弯曲。
d. 
当间隙为零时，金属和半
导体之间的电压全部降落在半导体内。因此产生了空间电荷区。
金属：电子海（失去电子，但海平面即费米能级不会发生很大变化）
半导体：电子气（量很少，易改变）
肖特基接触的势垒电容形式仍然与平行板电容类似：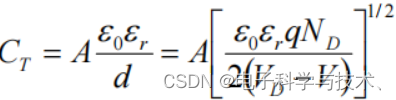
在此附上手稿能带图
8.2 金半接触的整流输运理论
8.2.1 扩散理论
平均自由程：相邻两次碰撞之间的平均距离，即称为载流子的平均自由程
扩散理论适用于：扩散长度＞＞平均自由程，和迁移率小的半导体
也就是说，载流子在势垒区输运时频繁碰撞
在此情况下，势垒宽度Xd是电压的函数。不仅势垒高度提高，而且宽度也相应增大，势垒宽度也称为势垒厚度。这种厚度依赖于外加电压的势垒称做肖特基势垒。
JSD:
J=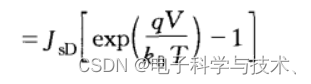
电流主要由e指数项决定
在正偏压下：忽略-1
在负偏压下，e指数很小可忽略，只剩-1。因此J=-JSD 而 JSD随电压变化，并不饱和。 因此金半接触的伏安特性曲线如下：
8.2.2 热电发射理论*（会推导）
适用于平均自由程＞＞势垒宽度
即在势垒区没有发生散射，电子在渡越过程中无碰撞
Ⅰ、半导体到金属的电流
我们可以得到：
2. 热电子向真空发射的理查逊常数A
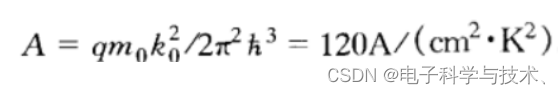
Ⅱ、金属到半导体
电子从金属到半导体所面临的势垒高度不随外加电压变化。所以，从金属到半导体的电子流所形成
的电流密度Jm-s是个常量，它应与热平衡条件下，即V=0时的Js-m大小相等方向相反
综上可得：
T：Theraml
——由热电子发射理论得到的伏-安特性式与扩散理论所得到的结果式形式上是一样的，所不同的是Jst与外加电压无关，但却是一个更强烈地依赖于温度的函数
——Ge、Si、GaAs都有较高的载流子迁移率，即有较大的平均自由程，因而在室温下，这些半导体材料的肖特基势垒中的电流输运机构，主要是多数载流子的热电子发射。
8.2.3 镜像力
镜像力是由于金属内正负电荷的感应作用，影响了半导体内的电势分布，对金属一侧的肖特基势垒产生影响（削减了势垒高度）
——上式表明，镜像力所引起的势垒降低量随反向电压的增加而缓慢地增大。当反向电压较高时，势垒的降低变得明显，镜像力的影响才显得重要。
8.2.4 隧道效应
临界厚度Xc：厚度大于Xc，电子不可隧穿势垒，厚度小于Xc，电子可以穿透势垒，引起势垒降低
势垒降低量：
它也随反向电压增加而增大。当反向电压较高时，势垒的降低才较明显。因此隧道效应对伏-安特性的影响和镜像力的影响基本相同。
镜像力和隧道效应对反向特性的影响特别显著，它们引起势垒高度的降低，使反向电流增加，而且随反向电压的提高，势垒降低更显著，反向电流也增加得更多。这样，理论结论与实际的反向特性就基本一致。
8.3 欧姆接触
—— 在金属－重掺杂半导体接触，一般ND = 10^19 /cm³ 宽度d ~ 100 Å
—— 电子会通过隧道效应通过势垒区
—— 在零偏压下，电流为零。也就是说此时金属半导体相互流过的电流相同，而从金属到半导体的电流为常数，因此用这个条件可以求Jms
—— 欧姆接触也叫做反阻挡层
求得总电流和电压关系：
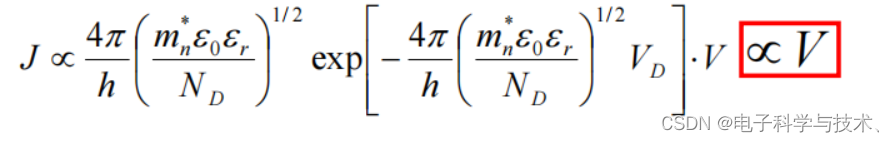
1. 接触电阻值很小
2. I-V关系是线性的，正反对称
扫一扫
4万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
