三、 半导体中的电子状态
本章重点在于理解和推倒等能面方程,掌握回旋共振实验,深入理解有效质量。
对于比较简单的空穴电子的导电机理本章将不再赘述,请读者自行翻看课本
3.1.1 半导体中电子的运动和有效质量
掌握能带结构的关键是确定E-k的关系(色散关系)


对于一个给定的半导体来说,E(k)的二阶导数项是个定值。写成经典关系式:

m*是电子的有效质量,具有质量单位。m*的表达式为:

m*在电子运动中比惯性质量m0更适用,且m*可以直接由回旋共振实验测得。
m*的意义,半导体中的电子需要同时响应内部势场和外加场的作用,有效质量概括了半导体内部势场对电子的作用,使得在解决半导体中电子在外力作用下的 运动规律时,可以不涉及到半导体内部势场的作用。
以第一布里渊区E-k关系为例。对其分别进行一次和二次求导取倒数,得到速度关系图和质量关系图:

在导带底,电子有正的有效质量;而在价带顶电子具有负的有效质量(此图要结合克朗尼格-朋奈模型分析)
在靠近布里渊区边界的地方,由于晶格衍射的影响E-k增速变换,数量关系将不再拟合抛物线。
我们可以得到以下结论:
——导带底能带越窄,k=0处曲率越小,二次微商越小,有效质量越大(正号,有效质量为正)
——价带顶能带越窄,曲线越舒缓。曲线曲率小,曲率半径大,有效质量越大(负号,有效质量为负)
——空穴在价带顶的有效质量为正值
3.1.2 电子的平均速度、加速度

(1)速度的正负与有效质量正负有关
(2)ħk=m*Vg称为电子的准动量
加速度:


3.2 回旋共振和等能面*
3.2.1 一般情况下的等能面方程

由上述方程形式可以看出:等能面是椭球面(椭球方程)
3.2.2 回旋共振实验(以各向同性晶体为例)
实验原理:通过改变磁场B的大小,使得电子回旋的频率等于高频电场的频率时,电场的能量会被
大量吸收,在图形上就会有一个吸收峰。通过频率ω和磁场B,就可以求得此各向同性晶体的有效
质量。

3.3 硅和锗的能带结构*
定义:
横有效质量(mt):垂直于椭球圆形截面的坐标轴方向的分量(一个)
纵有效质量(ml):平行于椭球圆形截面的坐标轴方向的分量(两个)
各向异性有效质量表达式

其中α,β,γ表示方向余弦。
其中椭球面可以分为完全等价的三组,1=2,3=4,5=6



图中看出价带顶有三条能带分别对应:重空穴,轻空穴,裂出空穴,其有效质量的大小是通过曲
率半径反映出来的
m*hh=0.53m0, m*lh=0.16m0,m3h=0.29m0;
锗:
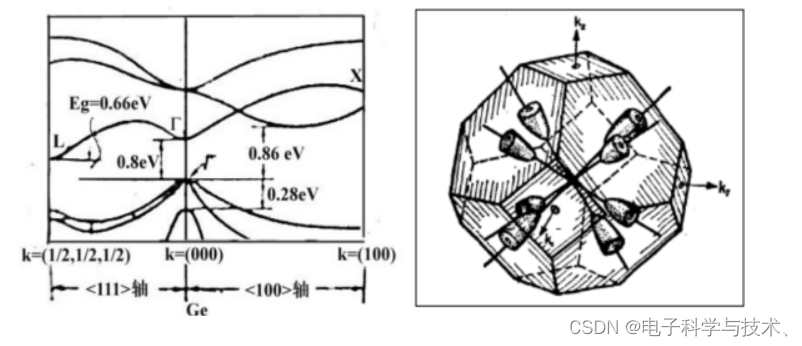
能带是半导体物理的精魄,硅是半导体行业的灵魂。
























 966
966

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








