树形结构+贪心思维 黑白树

题目描述：

一棵n个点的有根树，1号点为根，相邻的两个节点之间的距离为1。树上每个节点i对应一个值k[i]。每个点都有一个颜色，初始的时候所有点都是白色的。
你需要通过一系列操作使得最终每个点变成黑色。每次操作需要选择一个节点i，i必须是白色的，然后i到根的链上（包括节点i与根）所有与节点i距离小于k[i]的点都会变黑，已经是黑的点保持为黑。问最少使用几次操作能把整棵树变黑。

输入描述:

第一行一个整数n (1 ≤ n ≤ 10^5)
接下来n-1行，每行一个整数，依次为2号点到n号点父亲的编号。
最后一行n个整数为k[i] (1 ≤ k[i] ≤ 10^5)

输出描述:

一个数表示最少操作次数

---

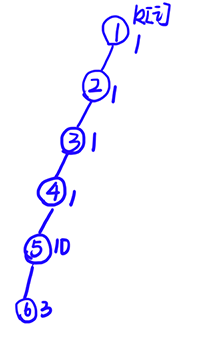
配合图片更好理解

因为第6个点必须涂色，所以涂了第6个点，第5.4个点也涂了，这个时候如果又从第3个点开始涂，明显是不优的，直接再涂第5个点就可以了；

所以只要维护每个结点子树的最大k值，还有每个结点可以往上涂的个数 f ，当f=0时，说明不能往上涂了，这时 f 直接更新为当前结点的 k 值；

代码：

#include<bits/stdc++.h>
#define LL long long
#define pa pair<int,int>
#define ls k<<1
#define rs k<<1|1
#define inf 0x3f3f3f3f
using namespace std;
const int N=100100;
const int M=50100;
const LL mod=1e9+7;
int n,head[N],cnt;
int k[N],f[N],ans;
struct Node{
	int to,nex;
}edge[N*2];
void add(int p,int q){
	edge[cnt].to=q,edge[cnt].nex=head[p],head[p]=cnt++;
}
void dfs(int p,int ft){
	for(int i=head[p];~i;i=edge[i].nex){
		int q=edge[i].to;
		if(q!=ft){
			dfs(q,p);
			f[p]=max(f[p],f[q]-1);
			k[p]=max(k[p],k[q]-1);
		}
	}
	if(f[p]==0){
		ans++;
		f[p]=k[p];
	}
}
int main(){
	memset(head,-1,sizeof(head));
	cin>>n;
	for(int i=2;i<=n;i++){
		int p;cin>>p;
		add(i,p),add(p,i);
	}
	for(int i=1;i<=n;i++) cin>>k[i];
	dfs(1,0);
	cout<<ans<<endl;
	return 0;
}