图论 tarjan算法入门总结

首先介绍下这个算法的用途：可用于求强连通，双连通，割点，割边等问题

关于算法的讲解

如果还不了解tarjan是什么可以先看上面的讲解。这篇只简单记录以便我复习。

目录

有向图强连通

割点

割边（桥）

无向图双连通分量

---

有向图强连通

概念：

连通图：有向图中任意两点都是连通的，则图被称为强连通图。 强连通分量指满足强连通条件的子图。

凡带“强”字的都是有向图，例如，强连通分量、强连通图。

入门问题：

有向图变为强连通图

找出所有的强连通分量， 缩点，统计缩点之后的新图的出度为0的点的个数（记为out)和入度为0的点的个数（记为in)

那么要加边的条数就是max(out,in)。

很简单的想法，入度出度为0时，一定是不满足强连通条件的。

而缩点就是tarjan算法中的color染色了，将颜色一样的缩为一个点。

模板：

#include<stdio.h>
#include<algorithm>
#include<stack>
#include<string.h>
#include<vector>
using namespace std;
#define ll long long
const int maxn=1000;
stack<int>s;
vector<int>e[maxn];
int dfn[maxn];
int low[maxn];
int vis[maxn];
int color[maxn];
int in[maxn],out[maxn];
int cnt=0,cnts=0;
int dfs(int u)
{
    dfn[u]=low[u]=++cnt;
    s.push(u);
    vis[u]=1;
    for(int i=0; i<e[u].size(); i++)
    {
        int v=e[u][i];
        if(!dfn[v])
        {
            dfs(v);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v])
            low[u]=min(low[u],low[v]);
    }
    if(dfn[u]==low[u])
    {
        color[u]=++cnts;
        vis[u]=0;
        while(s.top()!=u)
        {
            color[s.top()]=cnts;  //染色
            vis[s.top()]=0;
            s.pop();
        }
        s.pop();
    }
}

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        int a;
        while(~scanf("%d",&a)&&a)
            e[i].push_back(a);
    }
    for(int i=1; i<=n; i++)
        if(!dfn[i])
            dfs(i);
    memset(in,0,sizeof(in));
    memset(out,0,sizeof(out));
    for(int i=1; i<=n; i++)
    {
        for(int j=0; j<e[i].size(); j++)
        {
            int v=e[i][j];
            if(color[i]!=color[v])  //缩点
            {
                in[color[v]]++;
                out[color[i]]++;
            }
        }

    }
    int ans1=0,ans2=0;
    for(int i=1; i<=cnts; i++)
    {
        if(in[i]==0)
            ans1++;
        if(out[i]==0)
            ans2++;
    }
    if(cnts==1)
        printf("0\n");
    else
    printf("%d\n",max(ans1,ans2));
}

无向图变为

割点

概念：

在一个无向图中，如果有一个顶点集合，删除这个顶点集合以及这个集合中所有顶点相关联的边以后，图的连通分量增多，就称这个点集为割点集合。如果某个割点集合只含有一个顶点X（也即{X}是一个割点集合），那么X称为一个割点。

判断方法

1，根节点如果大于等于两颗子树，则根节点为割点，去掉根节点两棵子树无法连通。

2 ，非根节点维护两个数组dfn[]和low[]，dfn[u]表示顶点u被（首次）访问的顺序，low[u]表示u所在的连通分量中能回溯到的节点的min（dfn）。对于边(u, v)，如果low[v]>=dfn[u]，表示v只能通过u到达。此时u就是割点。

代码：

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<iostream>
using namespace std;
#define ll long long
const int maxn=105;
int dfn[maxn];
int low[maxn];
int book[maxn];
int head[maxn];
int cnt,num,root;
struct edge
{
    int v,next;
} e[maxn*maxn];
void add(int x,int y)
{
    e[cnt].v=y;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
void dfs(int x,int fa)
{
    dfn[x]=low[x]=++num;
    int cnts=0,k=0;
    for(int i=head[x]; i!=-1; i=e[i].next)
    {
        int to=e[i].v;
        if(to==fa&&k==0)  //由于是无向图，两个节点间如果存在两条边，不能全部跳过，如果再多条也当作一条处理，例如信号传递（路径唯一），则不能加！
        {
            k++;
            continue;
        }
        if(!dfn[to])
        {
            cnts++;   //统计x的子树的数量
            dfs(to,x);
            low[x]=min(low[x],low[to]);
            if(low[to]>=dfn[x]&&x!=root)  //非根节点
                    book[x]=1;    //x会被重复计算
            if(x==root&&cnts>=2)  //根节点
                book[x]=1;
        }
        else
            low[x]=min(low[x],dfn[to]);
    }
}
void init()
{
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(book,0,sizeof(book));
    memset(head,-1,sizeof(head));
    cnt=num=0;
}
int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m)&&(n||m))
    {
        init();
        int a,x;
        for(int i=0; i<m; i++)
        {
            scanf("%d %d",&a,&x);
            add(a,x);   //无向图
            add(x,a);
        }
        for(int i=1; i<=n; i++)
        {
            if(!dfn[i])   //如果没有遍历到过
            {
                root=i;
                dfs(i,-1);
            }
        }
        int sum=0;
        for(int i=1; i<=n; i++)
            if(book[i])
                sum++;
        printf("%d\n",sum);
    }
    return 0;
}

 

割边（桥）

概念

去掉某条边之后连通分量增加，则该边为割边。

判断方法

不需要考虑根节点，只需要判定low[v]>dfn[u]即可，原因与割点相同

代码：

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<vector>
using namespace std;
const int maxn=1005;
int low[maxn],dfn[maxn];
int cnt=0,sum=0,num=0;
struct node
{
    int v,next,c;
} e[maxn*maxn*2];
int head[maxn];
void add(int u,int v)
{
    e[num].v=v;
    e[num].next=head[u];
    e[num].c=0;
    head[u]=num++;
}
void dfs(int u,int fa)
{
//    printf("%d",u);
    low[u]=dfn[u]=++cnt;
    int k=0;
    for(int i=head[u]; i!=-1; i=e[i].next)
    {
        int to=e[i].v;
        /*虽是无向图，但再多条也当作一条处理，例如信号传递（路径唯一），则不加k==0的判断*/
        if(to==fa)
            continue;
        /*若是两点之间存在多条边，则需要判断只跳过一次
        if(to==fa&&k==0)
        {k++;
        continue;}
        */
        if(!dfn[to])
        {
            dfs(to,u);
//            printf("%d %d %d %d %d %d\n",u,to,dfn[u],low[u],dfn[to],low[to]);
            low[u]=min(low[u],low[to]);
            if(low[to]>dfn[u])
                e[i].c=e[i^1].c=1;
        }
        else
            low[u]=min(low[u],dfn[to]);
    }
}
void init()
{
    memset(low,0,sizeof(low));
    memset(dfn,0,sizeof(dfn));
    memset(head,-1,sizeof(head));
    cnt=0,sum=0,num=0;
}
int main()
{
    int n,m;
    while(scanf("%d %d",&n,&m)!=EOF)
    {
        init();
        int x,y;
        for(int i=0; i<m; i++)
        {
            scanf("%d %d",&x,&y);
            add(x,y);
            add(y,x);
        }
        for(int i=0; i<n; i++)
        {
            if(!dfn[i])
                dfs(i,i);
        }
        vector< pair<int,int> >a;  //将割边存入a并按从小到大排序输出
        for(int j=0; j<n; j++)
        {
            for(int i=head[j]; i!=-1; i=e[i].next)
            {
                if(e[i].c&&j<e[i].v)
                {
                    a.push_back(make_pair(j,e[i].v));
                    sum++;
                    e[i].c=e[i^1].c=0;  //清除
                }
            }
        }
        sort(a.begin(),a.end());
        printf("%d critical links\n",sum);
        for(int i=0; i<a.size(); i++)
            printf("%d - %d\n",a[i].first,a[i].second);
        printf("\n");
    }
    return 0;

}

 

无向图双连通分量

又分点双连通分量和边双连通分量两种。若一个无向图中的去掉任意一个节点（一条边）都不会改变此图的连通性，即不存在割点（桥），则称作点（边）双连通图。

边双连通：任意两个点至少存在两条边不相同（可以有相同点）的路径。

点双连通：任意两点间至少存在两条“点不重复”的路径。

无向图变为边双连通图

需要消除掉所有桥

首先将连通分量缩点（color染色），缩点之后新图为树，每个树枝都是桥，联通最少的点使其桥消除，最好的办法就是连接树叶，将两个树叶相连，则这两个树叶的路径中所有的节点都连通。

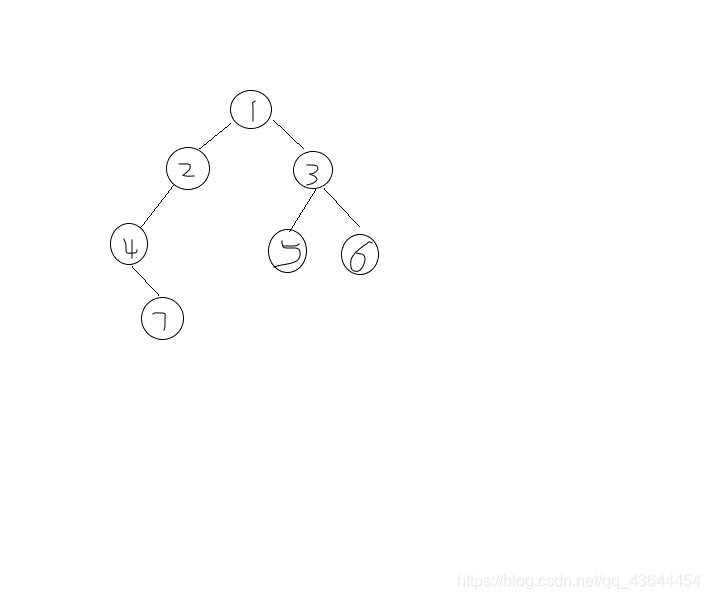
如图

连接5 7时，1 2 3 4 5 7全部联通，只剩3 6一个桥。然后将连通分量缩点，树变为1-6，1-6自然是桥，再将他们连接一条边即可。

由此可知，两个树叶节点用一条边可以消除，一个树叶节点也需要用一条鞭来消除，所以连接边得数量为（树叶数+1）/2；

树叶节点入度为1.

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<vector>
#include<stack>

using namespace std;
#define ll long long
const int maxn=100005;

int dfn[maxn],low[maxn],in[maxn];
vector<int>e[maxn];
int cnt,index;
void dfs(int u,int fa)
{
    low[u]=dfn[u]=++cnt;
    int k=0;
    for(int i=0; i<e[u].size(); i++)
    {
        int v=e[u][i];
        if(v==fa&&k==0)   //若是两点之间存在多条边，则需要判断只跳过一次
        {
            k=1;
            continue;
        }
        if(!dfn[v])
        {
            dfs(v,u);
            low[u]=min(low[u],low[v]);
        }
        else
            low[u]=min(low[u],dfn[v]);
    }


}
void init()
{
    memset(e,0,sizeof(e));
    memset(low,0,sizeof(low));
    memset(dfn,0,sizeof(dfn));
    memset(in,0,sizeof(in));
    cnt=index=0;
}
int main()
{
    int n,m,op=1;
    while(~scanf("%d %d",&n,&m)&&(n||m))
    {
        init();
        int x,y;
        for(int i=0; i<m; i++)
        {
            scanf("%d %d",&x,&y);
            e[x].push_back(y);
            e[y].push_back(x);
        }
        int sum=0;
        for(int i=1; i<=n; i++)
        {
            if(!dfn[i])
                dfs(i,-1);
        }
        for(int i=1; i<=n; i++)
        {
            for(int j=0; j<e[i].size(); j++)
            {
                int v=e[i][j];
                if(low[i]!=low[v])
                {
                    in[low[i]]++;
                    in[low[v]]++;
                }
            }
        }
        for(int i=1; i<=cnt; i++)
        {
            if(in[i]/2==1)  （由于是无向图，存图时正反各一次，所以这里树叶出现了两次）
                sum++;
        }
        sum=(sum+1)/2;
        printf("%d\n",sum);

    }
    return 0;
}