图论：tarjan算法

• 可以求有向图强连通分量个数，每个强连通分量的节点数等，还可以求割点和桥
• 强连通图G：G中任意两节点都可以相互到达
• 强连通分量：G不是强连通图，但G的子图G'是强连通图，则G'为G强连通分量。强连通分量是环。
• 割点：如果去掉图中节点v及与v相连的边后，图的强连通分量变多了，则v为割点
• 桥：如果去掉某条边后图的强连通分量变多了，则该条边为桥。
• 有割点不一定有桥，有桥一定有割点。如C为割点，但与C相连的边都不是桥。

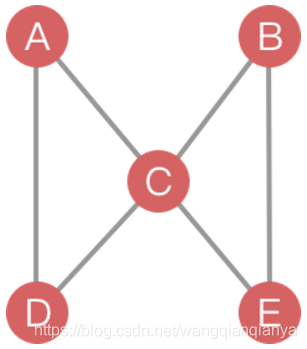
Tarjan 割点判断

tarjan算法是对DFS的优化，在dfs时割点的依据：

1. 如果一个节点是根节点，则如它的子节点数>1,则它为割点
2. 如果不是根节点，设为u,则若它的子节点中有一个节点v不能到达u的祖先节点，则u为割点。

Tarjan求强连通分量

1. dfn[] 数组：DFN[u]为节点 u 搜索的次序编号；可用来判断节点u是否被搜到过。
2. low[] 数组：表示该点能直接或间接到达时间最小的顶点。例如：low[u]为节点 u 或其子树能够追溯到最早的栈中节点的次序号；
3. stack 存储该连通子图中的所有点
4. scnt:存强连通分量个数
5. scc[]:记录每个节点属于的强连通分量编号

如：