手把手带你推导“高斯判别分析”核心公式

在机器学习的世界里，有许多强大的算法，它们如同一把把钥匙，帮助我们解锁数据背后的秘密。

今天，我们要聊的是一种非常有趣且实用的算法——高斯判别分析（Gaussian Discriminant Analysis，简称 GDA）。它不仅在分类任务中表现出色，还蕴含着深刻的数学原理。

接下来，我将手把手带你推导 GDA，从最基础的概念讲起，逐步深入，让你彻底掌握这个强大的工具。

一、什么是GDA？

高斯判别分析是一种基于概率生成模型的分类算法。它的核心思想是假设每个类别的数据都服从高斯分布（正态分布），并通过估计这些分布的参数来构建分类器。

与传统的判别分析（如线性判别分析 LDA）不同，GDA 更注重数据的生成过程，而不是直接寻找数据的分类边界。

图1. 数据分布

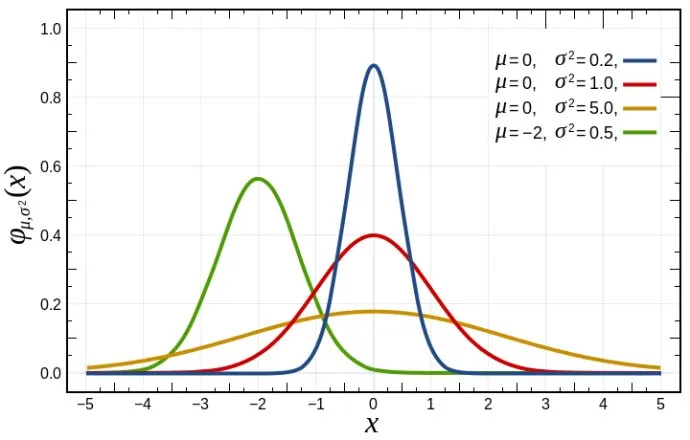
在深入 GDA 之前，我们先来复习一下高斯分布。

高斯分布（正态分布）是最常见的一种连续概率分布，其概率密度函数（PDF）如下：
$$p(x|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$
其中，$\mu$ 是均值，${\sigma }^2$ 是方差。

高斯分布的形状由这两个参数决定，均值决定了分布的中心位置，方差决定了分布的宽度。

GDA 适用于那些数据分布近似高斯分布的分类问题。

例如，在医学诊断中，某些疾病的症状指标可能服从高斯分布；在金融领域，股票价格的对数收益率也常常假设为高斯分布。

GDA 可以通过估计这些分布的参数，帮助我们更好地理解和预测数据。

二、GDA 的数学基础

在正式推导 GDA 之前，我们需要先了解一些数学基础。别担心，我会尽量用通俗易懂的方式来解释。

2.1 高斯分布参数估计

假设我们有一组数据 X={ x1,x2,…,xn}X = \{x_1, x_2, \ldots, x_n\}X={ x1​,x2​,…,xn​}，这些数据服从高斯分布 $N(\mu ,{\sigma }^2)$。

我们的目标是估计参数 $\mu$ 和 ${\sigma }^2$。

• 均值的估计：均值 $\mu$ 的最大似然估计（MLE）为：

$$\hat{\mu }=\frac{1}{n}\sum _{i=1}^n{x}_i$$

• 方差的估计：方差 ${\sigma }^2$ 的最大似然估计为：

σ^2=1n∑i=1n(xi−μ^)2 \hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \hat{\mu})^2 σ^2=n1​i=1∑n​(x