手把手带你推导“线性判别分析”核心公式

今天，我们来聊聊一个非常实用且有趣的算法——线性判别分析（Linear Discriminant Analysis，简称 LDA）。它不仅在分类任务中表现出色，还蕴含着深刻的数学思想。

接下来，我将手把手带你推导 LDA，从最基础的概念讲起，逐步深入，让你彻底掌握这个强大的工具。

一、LDA 是什么？

在正式推导之前，我们先来聊聊 LDA 是用来做什么的。简单来说，LDA 是一种监督学习的分类方法，它主要用于处理多类别分类问题。

它的目标是找到一种方式，将不同类别的数据在低维空间中尽可能地分开，同时将同一类别的数据尽可能地聚集在一起。

图1. 线性判别分析

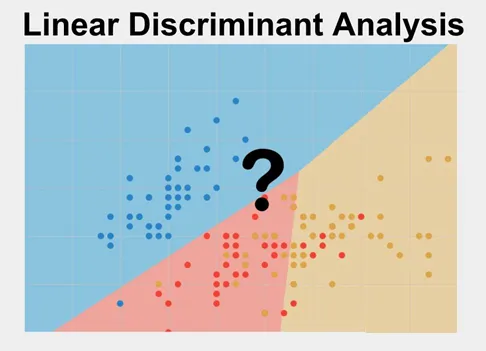
这听起来是不是有点像降维打击？没错，LDA 本质上也是一种降维技术，但它和 PCA（主成分分析）不同，LDA 是有监督的，它会利用类别标签来优化投影方向。

举个简单的例子，假设我们有一堆二维数据点，这些数据点属于多个不同的类别，如下图所示：我们可以看到，这些数据点在二维空间中是混杂在一起的，很难直接区分。

图2. PCA与LDA的示意图

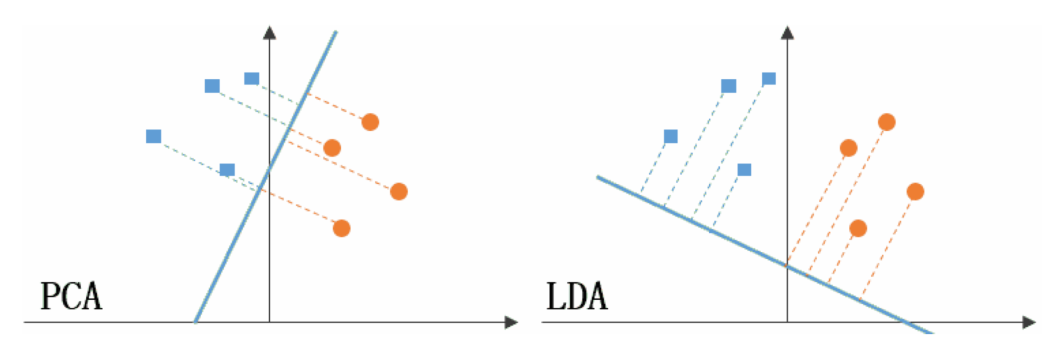
但如果我们将它们投影到一条直线上，情况可能会大不相同。

LDA 的目标就是找到这样一条直线，使得投影后的数据点在低维空间中能够更好地分开。

二、LDA 的数学基础

在深入推导之前，我们需要先了解一些数学基础。别担心，我会尽量用通俗易懂的方式来解释。

2.1 均值、方差

均值和方差是描述数据分布的两个重要指标。均值表示数据的中心位置，方差表示数据的离散程度。

对于一个数据集 X={ x1,x2,…,xn}X = \{x_1, x_2, \ldots, x_n\}X={ x1​,x2​,…,xn​}，均值 $\mu$ 和方差 ${\sigma }^2$ 的计算公式如下：

$$\mu =\frac{1}{n}\sum _{i=1}^n{x}_i$$

$${\sigma }^2=\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^2$$

在多维数据中，均值会变成均值向量，方差会变成协方差矩阵。协方差矩阵是一个对称矩阵，它描述了各个维度之间的相关性。

对于一个 $d$ 维数据集 $X$，协方差矩阵 $\Sigma$ 的计算公式如下：

$$\Sigma =\frac{1}{n}\sum _{i=1}^n(x_i-\mu )(x_i-\mu {)}^T$$

2.2 投影操作

投影是 LDA 的核心操作。假设我们有一个 $d$ 维数据点 $x$，我们想将它投影到一个一维直线上，这条直线的方向由单位向量 $w$ 决定。

那么，投影后的值 $y$ 可以表示为：

$$y=w^{T}x$$

这个公式的意思是，我们用 $w$ 作为基向量，将 $x$ 在这个方向上的分量提取出来。在二维空间中，这相当于将数据点投影到一条直线上；在更高维空间中，这相当于将数据点投影到一个低维子空间中。

三、LDA 的详细推导

接下来，我将更加详细地描述线性判别分析（LDA）的数学推导过程。

我们会从头到尾逐步推导，确保每一个步骤都清晰易懂。

3.1 优化目标

LDA 的目标是找到一个投影方向 $\mathbf{w}$，使得投影后的数据在低维空间中能够更好地分开。具体来说，我们需要最大化类间散度（between-class scatter），同时最小化类内散度（within-class scatter）。

用数学公式表示就是：

$$J(\mathbf{w})=$$