从SGD到Adam：优化算法的数学原理与应用

从经典的$SGD$算法到如今备受瞩目的$Adam$算法，这一段发展历程不仅是技术的演进，更是人类智慧与机器智能深度交融的生动写照。

今天，就让我们深入探讨$SGD$和$Adam$的数学原理，分析其在实际应用中的优缺点，为神经网络训练中优化算法的选择提供参考依据。

一、随机梯度下降（$SGD$）算法

随机梯度下降（$SGD$）算法是神经网络优化的基础算法之一，其核心思想是通过随机选择一个样本或一个小批量样本，计算损失函数在这些样本上的梯度，从而近似整个数据集的梯度，进而更新模型参数。

这种方法不仅减少了计算量，还提高了训练速度，使得$SGD$在处理大规模数据集时尤为高效。

图1. 梯度下降算法

$SGD$的原理是基于梯度下降法，通过迭代更新参数，逐步逼近损失函数的最小值。其更新公式为：
$${\theta }_{t+1}={\theta }_t-\eta {\nabla }_{\theta }L({\theta }_t;x_i,y_i)$$
其中，$\eta$ 是学习率，${\theta }_t$ 是第 $t$ 次迭代的参数，${\nabla }_{\theta }L({\theta }_t;x_i,y_i)$ 是在样本 $(x_i,y_i)$ 上计算的梯度。

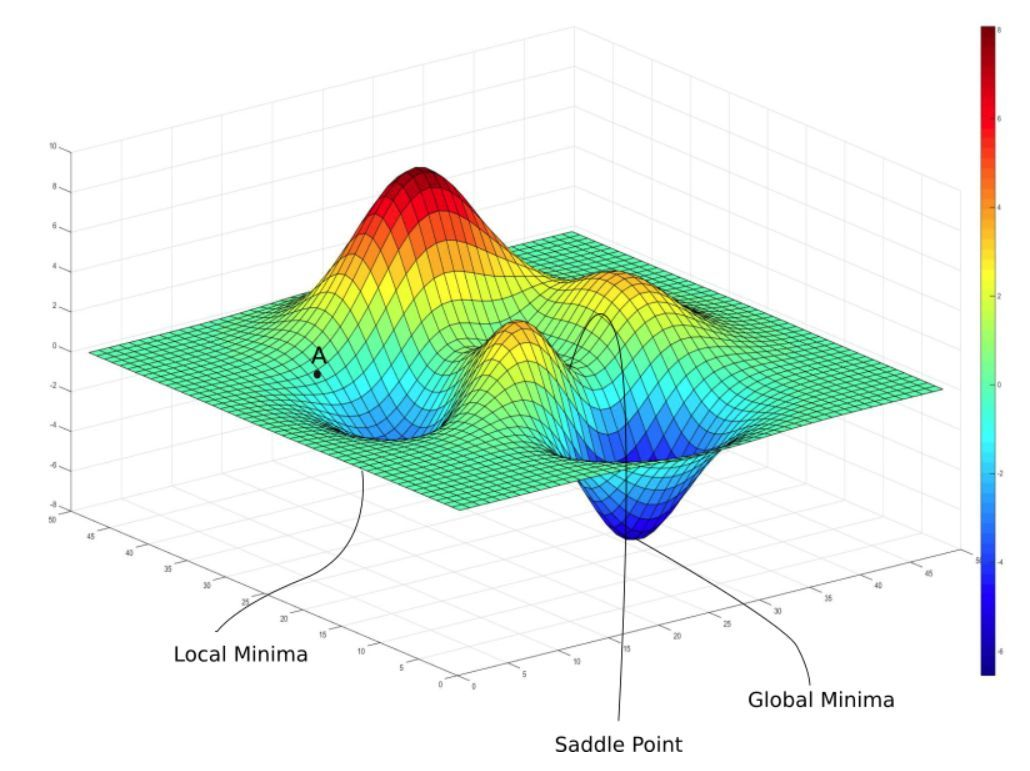
$SGD$通过这种方式，利用随机性引入的噪声帮助模型跳出局部最小值，从而在某些情况下能够找到更优的全局最小值。

$SGD$的简单高效的特点使其在早期神经网络训练中得到了广泛应用，尤其是在数据量较大且模型复杂度较高的场景下，$SGD$能够有效地加速训练过程，提高模型的收敛速度。

---

$SGD$的收敛性分析是其理论研究的核心内容之一，其收敛性主要取决于学习率的选择和梯度的稳定性。

理论上，$SGD$在满足特定条件下能够收敛到损失函数的全局最小值或局部最小值。对于凸优化问题，$SGD$在合适的学习率设置下可以收敛到全局最小值。

具体来说，如果学习率满足以下条件：
$$\sum _{t=1}^{\infty }{\eta }_t=\infty \text{和}t=1$$