Laplacian算子
Laplacian算子简单来说就是二阶导数
对于图上的拉普拉斯算子,我们要明确:
1.图上的函数是什么
2.图上的一阶导数是什么
3.图上的二阶导数是什么
定义
1.图上的函数定义为 f f f ,对于图上的任意节点 i i i , f ( i ) f(i) f(i) 为节点 i i i 上的出度
2.
f
f
f 在节点
i
i
i 沿
j
j
j 出度方向的导数
f
′
(
i
,
j
)
=
f
(
i
)
−
f
(
j
)
f'(i,j)=f(i)-f(j)
f′(i,j)=f(i)−f(j)
3.
f
f
f 在节点
i
i
i 上的二阶导数为:节点
i
i
i 出度方向的导数 - 所有节点
i
i
i 入度方向的导数
f
′
′
(
i
)
=
∑
m
∼
i
f
′
(
i
,
m
)
−
∑
i
∼
n
f
′
(
n
,
i
)
f''(i) = \sum_{m \sim i} f'(i,m) - \sum_{i \sim n} f'(n,i)
f′′(i)=m∼i∑f′(i,m)−i∼n∑f′(n,i)
公式自己编的感觉他们的表达方式都不对
举例
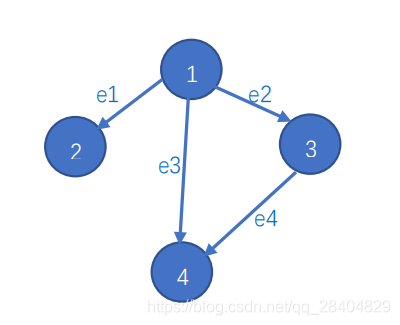
STEP 1.
f ( 1 ) = 3 f ( 2 ) = 0 f ( 3 ) = 1 f ( 4 ) = 0 f(1)=3 \quad f(2)=0 \quad f(3)=1 \quad f(4)=0 f(1)=3f(2)=0f(3)=1f(4)=0
STEP 2.
f
′
(
1
,
2
)
=
3
f
′
(
1
,
3
)
=
2
f
′
(
1
,
4
)
=
3
f'(1,2)=3 \quad f'(1,3)=2 \quad f'(1,4)=3
f′(1,2)=3f′(1,3)=2f′(1,4)=3
f
′
(
3
,
4
)
=
1
f'(3,4)=1
f′(3,4)=1
STEP 3.
f
′
′
(
1
)
=
f
′
(
1
,
2
)
+
f
′
(
1
,
3
)
+
f
′
(
1
,
4
)
=
3
+
2
+
3
=
8
f''(1)=f'(1,2)+f'(1,3)+f'(1,4)=3+2+3=8
f′′(1)=f′(1,2)+f′(1,3)+f′(1,4)=3+2+3=8
f
′
′
(
2
)
=
−
f
′
(
1
,
2
)
=
−
3
f''(2)=-f'(1,2)=-3
f′′(2)=−f′(1,2)=−3
f
′
′
(
3
)
=
f
′
(
3
,
4
)
−
f
′
(
1
,
3
)
=
1
−
2
=
−
1
f''(3)=f'(3,4)-f'(1,3)=1-2=-1
f′′(3)=f′(3,4)−f′(1,3)=1−2=−1
f
′
′
(
4
)
=
−
f
′
(
1
,
4
)
−
f
′
(
3
,
4
)
=
−
3
−
1
=
−
4
f''(4)=-f'(1,4)-f'(3,4)=-3-1=-4
f′′(4)=−f′(1,4)−f′(3,4)=−3−1=−4
一个比较有意思的推导
f = [ 3 0 1 0 ] f = \begin{bmatrix} 3 \\ 0 \\ 1 \\ 0 \end{bmatrix} f=⎣⎢⎢⎡3010⎦⎥⎥⎤ \quad 关联矩阵 K = [ 1 1 1 0 − 1 0 0 0 0 − 1 0 1 0 0 − 1 − 1 ] K = \begin{bmatrix} 1 & 1 & 1 & 0 \\ -1 & 0 &0 & 0\\ 0 & -1 &0 & 1\\ 0 & 0 & -1 & -1 \end{bmatrix} K=⎣⎢⎢⎡1−10010−10100−1001−1⎦⎥⎥⎤
K T f = [ 1 − 1 0 0 1 0 − 1 0 1 0 0 − 1 0 0 1 − 1 ] [ 3 0 1 0 ] = [ f ′ ( 1 , 2 ) f ′ ( 1 , 3 ) f ′ ( 1 , 4 ) f ′ ( 3 , 4 ) ] = [ 3 2 3 1 ] K^Tf=\begin{bmatrix} 1 & -1 & 0 & 0 \\ 1 & 0 &-1 & 0\\ 1 & 0 &0 & -1\\ 0 & 0 & 1 & -1 \end{bmatrix}\begin{bmatrix} 3 \\ 0 \\ 1 \\ 0 \end{bmatrix}=\begin{bmatrix} f'(1,2) \\ f'(1,3) \\ f'(1,4) \\ f'(3,4) \end{bmatrix}=\begin{bmatrix} 3 \\ 2 \\ 3 \\ 1 \end{bmatrix} KTf=⎣⎢⎢⎡1110−10000−10100−1−1⎦⎥⎥⎤⎣⎢⎢⎡3010⎦⎥⎥⎤=⎣⎢⎢⎡f′(1,2)f′(1,3)f′(1,4)f′(3,4)⎦⎥⎥⎤=⎣⎢⎢⎡3231⎦⎥⎥⎤
K K T f = [ 1 1 1 0 − 1 0 0 0 0 − 1 0 1 0 0 − 1 − 1 ] [ f ′ ( 1 , 2 ) f ′ ( 1 , 3 ) f ′ ( 1 , 4 ) f ′ ( 3 , 4 ) ] = [ f ′ ( 1 , 2 ) + f ′ ( 1 , 3 ) + f ′ ( 1 , 4 ) − f ′ ( 1 , 2 ) − f ′ ( 1 , 3 ) + f ′ ( 3 , 4 ) − f ′ ( 1 , 4 ) − f ′ ( 3 , 4 ) ] = [ 8 − 3 − 1 4 ] KK^Tf=\begin{bmatrix} 1 & 1 & 1 & 0 \\ -1 & 0 &0 & 0\\ 0 & -1 &0 & 1\\ 0 & 0 & -1 & -1 \end{bmatrix}\begin{bmatrix} f'(1,2) \\ f'(1,3) \\ f'(1,4) \\ f'(3,4) \end{bmatrix}=\begin{bmatrix} f'(1,2) + f'(1,3) +f'(1,4) \\ -f'(1,2) \\ - f'(1,3) + f'(3,4) \\ -f'(1,4) - f'(3,4) \end{bmatrix} = \begin{bmatrix} 8 \\ -3 \\ -1 \\ 4 \end{bmatrix} KKTf=⎣⎢⎢⎡1−10010−10100−1001−1⎦⎥⎥⎤⎣⎢⎢⎡f′(1,2)f′(1,3)f′(1,4)f′(3,4)⎦⎥⎥⎤=⎣⎢⎢⎡f′(1,2)+f′(1,3)+f′(1,4)−f′(1,2)−f′(1,3)+f′(3,4)−f′(1,4)−f′(3,4)⎦⎥⎥⎤=⎣⎢⎢⎡8−3−14⎦⎥⎥⎤
另一个比较有意思的推导
定义
D
D
D 为
N
∗
N
N*N
N∗N 的度数矩阵(degree matrix)
D
(
i
,
j
)
=
{
d
i
,
if
i
=
j
0
,
otherwise
D(i,j) = \begin{cases} d_i, & \text{if $i=j$ } \\ 0, & \text{otherwise} \end{cases}
D(i,j)={di,0,if i=j otherwise
定义
A
A
A 为
N
∗
N
N*N
N∗N 的邻接矩阵(adjacency matrix)
A
(
i
,
j
)
=
{
1
,
if
x
i
∼
x
j
0
,
otherwise
A(i,j) = \begin{cases} 1, & \text{if $x_i \sim x_j$ } \\ 0, & \text{otherwise} \end{cases}
A(i,j)={1,0,if xi∼xj otherwise
Laplacian算子可以写成
L
=
D
−
A
=
[
3
0
0
0
0
1
0
0
0
0
2
0
0
0
0
2
]
−
[
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
]
=
[
3
−
1
−
1
−
1
−
1
1
0
0
−
1
0
2
−
1
−
1
0
−
1
2
]
L=D-A=\begin{bmatrix} 3 & 0 & 0 & 0 \\ 0 & 1 &0 & 0\\ 0 & 0 &2 & 0\\ 0 & 0 & 0 & 2 \end{bmatrix} - \begin{bmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 &0 & 0\\ 1 & 0 &0 & 1\\ 1 & 0 & 1 & 0 \end{bmatrix} = \begin{bmatrix} 3 & -1 & -1 & -1 \\ -1 & 1 &0 & 0\\ -1 & 0 &2 & -1\\ -1 & 0 & -1 & 2 \end{bmatrix}
L=D−A=⎣⎢⎢⎡3000010000200002⎦⎥⎥⎤−⎣⎢⎢⎡0111100010011010⎦⎥⎥⎤=⎣⎢⎢⎡3−1−1−1−1100−102−1−10−12⎦⎥⎥⎤
而:
K
K
T
=
[
1
1
1
0
−
1
0
0
0
0
−
1
0
1
0
0
−
1
−
1
]
[
1
−
1
0
0
1
0
−
1
0
1
0
0
−
1
0
0
1
−
1
]
=
[
3
−
1
−
1
−
1
−
1
1
0
0
−
1
0
2
−
1
−
1
0
−
1
2
]
KK^T=\begin{bmatrix} 1 & 1 & 1 & 0 \\ -1 & 0 &0 & 0\\ 0 & -1 &0 & 1\\ 0 & 0 & -1 & -1 \end{bmatrix}\begin{bmatrix} 1 & -1 & 0 & 0 \\ 1 & 0 &-1 & 0\\ 1 & 0 &0 & -1\\ 0 & 0 & 1 & -1 \end{bmatrix}=\begin{bmatrix} 3 & -1 & -1 & -1 \\ -1 & 1 &0 & 0\\ -1 & 0 &2 & -1\\ -1 & 0 & -1 & 2 \end{bmatrix}
KKT=⎣⎢⎢⎡1−10010−10100−1001−1⎦⎥⎥⎤⎣⎢⎢⎡1110−10000−10100−1−1⎦⎥⎥⎤=⎣⎢⎢⎡3−1−1−1−1100−102−1−10−12⎦⎥⎥⎤
😉 拉普拉斯算子等于离散拉普拉斯矩阵
K K T = L = D − A KK^T=L=D-A KKT=L=D−A
参考:
https://www.bilibili.com/video/av51204684?p=7
https://zhuanlan.zhihu.com/p/54505069
























 1238
1238

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








