G2O initial guess 方法的选择

最新推荐文章于 2025-09-21 09:11:35 发布

原创

最新推荐文章于 2025-09-21 09:11:35 发布 · 986 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#linux #c++ #经验分享

本文探讨了G2O库中不同的初始化方法对优化结果的影响，通过源码解析和编程验证，比较了使用生成树和里程计进行初始猜测的效果。

G2O initial guess 方法的选择

〇、前言

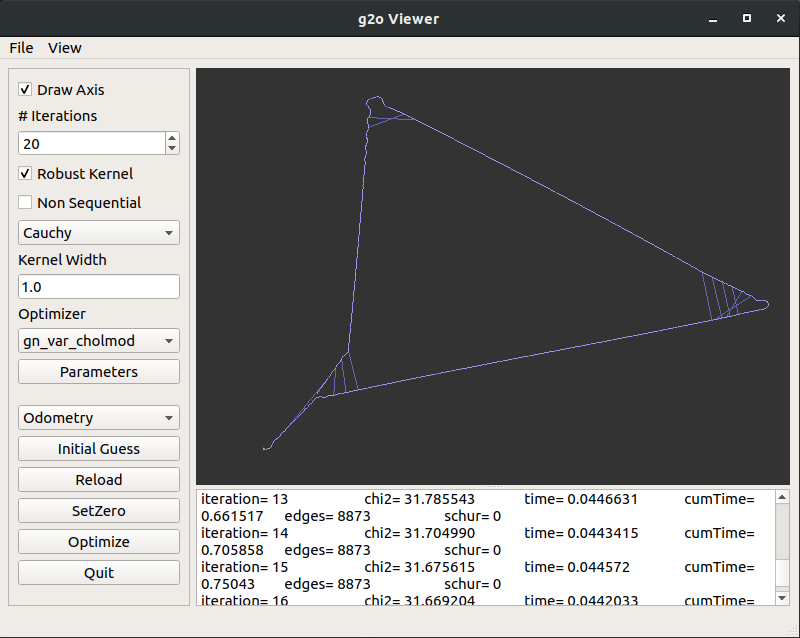
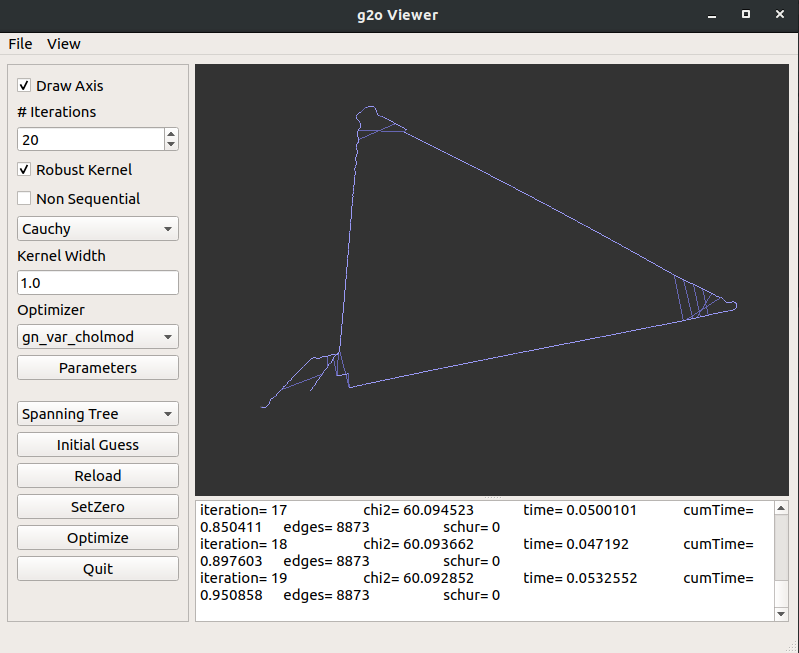
由于不同优化初始化方法会对g2o的结果产生影响，如下图所示，在勾选Robust Kernel的条件下:using initial guess from spanning tree 和 using initial guess from odometry 在其他设置相同的情况下得到的优化结果差别很大。因此我们希望可以通过程序来选择合适的优化初值设置方法。

PS：这里产生差异的原因和是否勾选Non Sequential也相关，用spanning tree初始化时若勾选Non Sequential会得到与左图相同的结果，而No Sequential的意思是只把回环边设置为鲁棒核

一、查看对应源码

由于没有搜索到相关资料，所以最好的方式就是查看g2o_viewer的源码。(同样的事已经做过一次，只是记性不好，这也是写这篇博客的原因)。

首先通过QT Designer查到对应下拉框的名字叫cbxIniitialGuessMethod，按钮btnInitialGuess

再找到对应的响应函数，然后就是我们需要的代码。

void MainWindow::on_btnInitialGuess_clicked()
{
   
   
  if (viewer->graph->activeEdges().size() == 0)
    viewer->graph->initializeOptimization();

  switch (cbxIniitialGuessMethod->currentIndex()) {
   
   
    case 0:
      // spanning tree
      viewer->graph->computeInitialGuess();
      break;
    case 1:
      // odometry
      {
   
   
        EstimatePropagatorCostOdometry costFunction(viewer->graph);
        viewer->graph->computeInitialGuess(costFunction);
      }
      break;
    default:
      cerr << __PRETTY_FUNCTION__ << " Unknown initialization method" << endl;
      break;
  }
  viewer->setUpdateDisplay(true);
  viewer->update();
}

二、编程验证

2.1 g2o_test.cpp

#include <iostream>
#include <fstream>
#include <stdio.h>
#include <vector>
#include <numeric>
#include <sstream>
//用于构建和计算图优化 g2o
#include <g2o/types/slam3d/types_slam3d.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
<