分数阶神经网络在量化交易中的应用

基于分数阶神经网络和深度Q网络的量化基金交易研究

摘要

量化基金交易策略能够帮助投资者更有效地降低风险并最大化自身收益。本文利用分数阶神经网络和深度Q学习网络进行交易决策。首先，为了使深度Q学习网络更快收敛，提出了一种新的数据预处理方法。使用预处理后的数据训练分数阶神经网络，并采用改进的梯度更新方法更新网络参数。然后，通过符号分离法解决负数无分数次幂的问题。最后，训练好的深度Q学习网络可做出交易决策并获得一定收益。交易结果表明，所提出的方法是有效的，且优于传统方法。

关键词 ：量化基金交易；分数阶微积分（FOC）；深度Q学习网络。

I. 引言

基金市场一直是一个热点。大多数学者和投资者都在探索基金价格预测。目前，基金交易策略的预测方法是先预测未来的单位净值（NAV），然后根据单位净值手动确定交易策略。通常使用BP神经网络来预测未来的NAV[1‐4]。

基金交易策略预测是一种时间序列预测。基金市场系统中存在离散和非线性因素，这些因素导致单位净值预测误差较大。在预测未来三天的单位净值时，预测第二天的值需要依赖第一天的预测结果；而预测第一天的值又需要使用当天的实际单位净值。这会导致累积误差，然后基于单位净值人工确定交易策略。由于蝴蝶效应的存在，所得到的策略效果非常差。

分数阶微积分的最大优势在于其记忆性和传递性。将分数阶微积分引入神经网络用于预测基金净值，能够增强网络的记忆能力，降低因其离散性和非线性所导致的预测结果高误差。为了减少预测值的累积误差，采用BP和DQN来预测基金的交易决策而非单位净值，从而使交易策略更加稳健。

第二部分介绍了训练网络所需的数据类型。本文中采用最大差值法用于将一维无标签数据转换为四维有标签数据。这决定了预训练网络训练的可行性。第三部分介绍了使用处理后的基金数据训练神经网络的方法和步骤。通过分数阶微积分推导出一种新的梯度更新方法。但由于负数没有分数次幂，本文提出了符号分离法。将传统神经网络与分数阶神经网络进行了比较。第四部分介绍了利用预训练模型的参数在原始基金数据集上进行DQN训练的方法和步骤。第五部分是本文的总结。

II. 数据预处理

A. 预备知识

通过低价买入和高价卖出可以在基金交易中获利。收益率可以用以下公式表示[5]：

$$
R = E - (BE \times S)
\quad (1)
$$

其中，R为收益，E为权益，B为购买时每单位净值，S为卖出时每单位净值。

然而，仅用收益来表达并不理想，因为它还与时间相关。我们引入了收益率，其公式如下：

$$
R_r = \frac{R}{T}
\quad (2)
$$

其中，$ R_r $ 为收益率，T为基金的持有时间。

数据是一个一维数组。如表(1)所示。它不能直接使用，因为没有关于买入、卖出和持有的信息。

Date	8/26	8/27	8/28	8/31	9/1	9/2
值	1.394	1.409	1.431	1.432	1.442	1.446

表I. 部分数据样本

基金代码为000001的基金部分数据样本

金融市场通常使用移动平均（MA）来观察市场[6]。它使用统计学中的“移动平均”原理，将一段时间内股票价格的平均值连接成一条曲线，用于显示股票价格的历史波动，并反映未来股价指数的趋势。

例如，MA5代表过去五天的平均收盘价。目前，股票市场通常使用MA5、MA10、MA20等数据指标绘制曲线以辅助观察。因此，窗口大小设置为10天，这决定了神经网络的输入层大小。

以10天为窗口大小，输入向量为十维。输出向量为三维，表示三种操作。第一维表示是否买入，第二维表示是否卖出，第三维表示是否持有。例如(1,0,0)是卖出操作。

B. 数据预处理方法

因为收益率是单位净值与时间之间的差值。因此，我们的目的是找出这些数据的差值，并找到具有最大斜率的点对。这被称为最大差值（MD）。假设该基金有n个数据。步骤如下：

1) 读取基金数据并赋值给F。
2) 初始化n × n的零矩阵D和G。
3) 初始化空队列GL和L。
4) i = 0
5) WHILE i < n
a) j = 0
b) WHILE j < n
D[i][j] = F[i] – F[j]
G[i][j] = D[i][j] / (i – j)
将G[i][j], i, j加入GL
j = j + 1
c) i = i + 1
6) 将GL中的元素按降序排序。
7) 若L为空
a) GL出队，并将该元素添加到L队列的尾部。
8) 否则
a) GL出队，出队元素的i, j值构成闭区间[i, j]。
b) 判断该区间是否与L中任意元素的区间[i, j]存在交集。
c) 若存在交集，则丢弃该元素。
d) 否则，将该元素添加到L的尾部。
9) L中的所有元素即为满足条件的点对。

使用上述方法获取带标签的数据，并使用’matplot’绘制下图。

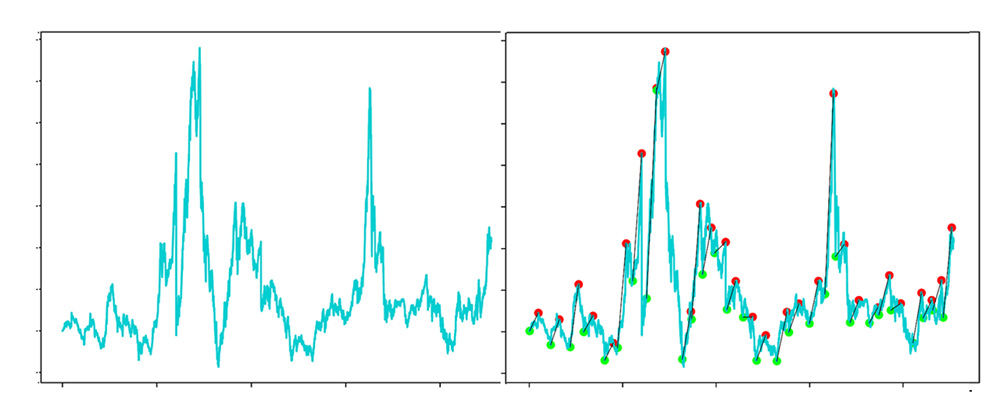
现在，我已将原始的一维数据转换为四维数据。例如，第一天的数据是(1,1,0,0)。第一个1表示单位净值（净资产值）为1，第二个数据1表示买入，第三个数据0表示不卖出，第四个数据0表示不持有。最后三个维度是动作向量，并且采用独热编码。

III. 预训练网络

A. 预训练模型的功能

在线交易基金决策训练。我们可以直接采用随机交易的方法，让DQN网络学习可靠的交易策略。在随机交易中，存在大量状态，这会导致收敛速度慢、训练时间长，甚至可能无法收敛。另一个原因是DQN在学习过程中使用了自举法，从而导致过高估计。如果在初始阶段使用随机探索，容易造成过高估计，进而导致模型训练失败[7][8]。

B. 预训练神经网络设计

本文可以采用一个10 × 8 × 5 × 3全连接网络。

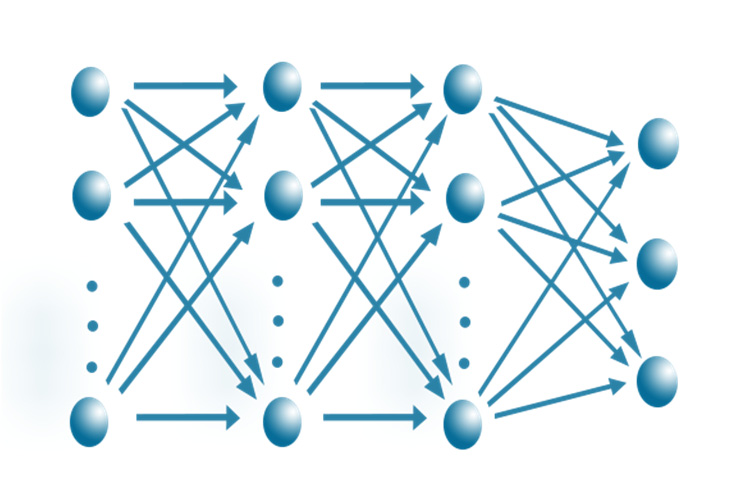
输入层是窗口大小（10天为一个窗口）的数据，最后三个节点是一个独热编码向量。第一维表示是否买入，第二维表示是否卖出，第三维表示是否持有。

C. 使用传统方法训练预训练网络

在训练中。神经网络的前向传播过程中使用了ReLU函数。使用梯度下降法(GD)更新权重。

学习率r的初始值为0.001。并且在每个训练周期中，学习率r变为前一个训练周期的十分之一。

因为买卖样本相对较小。在训练过程中，输出值会增加。这将在梯度更新中优先考虑准确性。

所有数据约为4000天。我使用了前3500天的数据进行训练。经过20轮训练后，神经网络具备了一定的操作基金的能力。操作过程如下表‐2所示。

Date	操作	资产	NVA
2016年5月19日	buy	99850.0	1.059
2020年2月10日	sell	104698.24	1.116
2020年2月11日	buy	104541.19	1.128
2020年9月4日	hold	133178.80	1.43

表二。使用传统BP的交易详情

最近4年。使用100000元传统BP网络进行自动交易。收入为33178.80元。

D. 使用新方法训练预训练网络

神经网络的前向传播和误差反向传播与4.3.1节完全相同。然而，使用阶数𝛼的偏导数来更新W，并使用GL型分数阶微积分[9][10]。

$$
\frac{\partial E}{\partial W} = \frac{\partial E}{\partial O} \cdot \frac{\partial O}{\partial W}
\quad (3)
$$

$$
\frac{\partial E}{\partial W} = -\frac{\Gamma(3)}{\Gamma(3-\alpha)}(Y-O)^{2-\alpha} \cdot \frac{\partial O}{\partial W}
\quad (4)
$$

$$
\frac{\partial E}{\partial W} = -\frac{2}{(2-\alpha)}
\quad (5)
$$

引入分数阶导数来更新权重。存在负数计算分数次幂的问题。

我们知道，负数在实数范围内没有分数次幂的定义。

我通过符号分离法解决了负数没有分数次幂的问题：假设要计算分数次幂的矩阵为W，$ W_{ij} $ 是W中的元素，可能为正或负。

1) 计算输入矩阵的符号矩阵：$ S_{ij} = sign(W_{ij}) $
2) 计算输入矩阵的绝对值矩阵：$ W’ {ij} = abs(W {ij}) $
3) 计算绝对值矩阵的k次幂：$ T_{ij} = pow(W’ {ij}, k) $
4) 计算最终结果：$ R {ij} = T_{ij} * S_{ij} $（其中*表示矩阵对应元素相乘）

问题之后没有分数指数幂。现在我们可以使用改进方法进行训练。其中，训练周期是迭代次数，a是分数阶的阶数。

训练过程的伪代码：

1) begin
2) epoch = 0, i = 10, a = 0.1, best = a, record = 0
3) WHILE a < 2
a) WHILE 训练周期 < 20
使用新方法训练神经网络。
训练周期 = 训练周期 + 1
b) 在测试集上测试决策并计算奖励。
c) 如果奖励 > 记录
最优值 = a
a = a + 0.01
4) End.

训练过程中仅修改了导数的阶数，学习率和训练数据保持不变。当𝛼为0.86时，分数阶神经网络获得最大收益。

操作过程如下面的表‐3所示。

Date	操作	资产	NVA
2016年5月19日	buy	99850.0	1.009
2020年2月12日	sell	108704.88	1.104
2020年2月13日	buy	108541.83	1.076
2020年9月4日	hold	134259.37	1.43

表III. 使用传统BP的交易详情

近4年。使用100000元分数阶BP网络进行自动交易。收入为34259.37元。

E. 比较两个网络

通过比较两个预训练网络。它们都具有一定的决策能力，并能带来一定的收益。然而，使用分数阶神经网络的方法比传统方法可以获得更高的收益，收益增加了1000元。

IV. 使用DQN继续训练

A. 使用DQN继续学习操作基金交易

具有这些参数的初始DQN可以大大缩短模型[11][12]的收敛时间。

模型的训练步骤：
1) 创建一个与预训练网络相同的DQN。
2) 使用预训练模型的参数初始化DQN。
3) 初始资金、手续费、学习率、奖励衰减因子 $\gamma$、总训练轮数、迭代指导数n、经验队列EL。
4) 获取第t天的状态并记录为 $ s_t $。
5) 生成一个随机数M，$ M \in (0,e) $。
6) 如果M < i
a) 随机生成一个动作 $ a_t $。
7) 否则
a) 使用DQN预测一个操作 $ a_t $。
8) 执行动作。
9) 如果当前周期 < n
a) 如果操作为买入 $ r_t = \text{fee} $
b) 如果操作为卖出 $ r_t = \text{profit} $
c) 如果操作为持有 $ r_t = -100 $
10) 否则
a) 如果操作为买入 $ r_t = \text{fee} $
b) 如果操作为卖出 $ r_t = \text{profit} $
c) 如果操作为持有 $ r_t = 0 $
11) 获取第t天的状态+1并将其记录为 $ s_{t+1} $。
12) 使用DQN预测 $ s_{t+1} $ 的 $ a_{t+1} $ 并将 $ a_{t+1} $ 向量的最大值记录为max。
13) 目标 $ y = r_t + \gamma \cdot \text{max} $。
14) 使用DQN预测 $ s_t $ 的 $ a’ t $，将 $ a_t $ 中最大值的位置记录为mp，并将 $ a_t $ 中mp位置的值更新为y。
15) DQN使用 $ s_t $ 和 $ a’_t $ 进行梯度更新。
16) 将 $ s_t, a_t, s {t+1}, a_{t+1} $ 作为一个元素追加到EL中。
17) 当一个训练周期完成时，从EL中采样数据，并使用采样数据更新DQN的参数。

第t天的状态s是获取第t天的单位净值以及从第T-1天到第T-9天共十天的单位净值数据。当完成一个训练周期后，从经验回放缓冲区中采样数据，并使用采样数据更新DQN的参数。在训练过程中，学习率r的初始值为0.001，且每个训练周期中学习率r变为上一周期的十分之一。

奖励衰减因子（$\gamma$）被设置为0.9。总的训练周期数（e）被设置为100。每次迭代后采样1000个数据样本进行经验回放。训练过程如图3所示。

如图3所示，在前80个训练轮次中，使用了降低概率的随机搜索。最后20个训练轮次完全由DQN进行交易。其平均收益约为50000元。这优于仅使用预训练网络。

V. 结论

使用预训练模型的方法替代随机探索方法，以获得更快的收敛效果。采用最大差值法对数据进行预处理，以便训练预训练模型。在预训练模型中，使用分数步长更新方法替代整数阶，其效果优于整数阶。