加权SPICE算法用于单比特雷达成像

加权SPICE算法用于单比特汽车雷达的距离‐多普勒成像

尚晓磊，李健，IEEE会士，以及佩特雷·斯托伊卡，IEEE会士

摘要

本文研究了利用单比特ADC采样并结合接收机端时变阈值的单比特汽车LFMCW1或PMCW雷达进行距离‐多普勒成像的问题。一位采样技术可显著降低汽车雷达系统的成本和功耗。我们将单比特LFMCW/PMCW雷达的距离‐多普勒成像问题建模为单比特稀疏参数估计问题。近期提出的无超参数（因而易于使用）加权SPICE算法，包括SPICE、LIKES、SLIM和IAA，在高精度采样数据下表现出优异的参数估计性能。然而，这些算法无法直接用于单比特数据。本文首先提出一种正则化最小化算法，称为1bSLIM，用于单比特雷达系统下的精确距离‐多普勒成像。接着，我们阐述如何将SPICE、LIKES和IAA算法扩展至单比特数据情况，并将这些扩展版本分别命名为1bSPICE、1bLIKES和1bIAA。这些单比特无超参数算法被统一纳入一比特加权SPICE框架中。此外，还研究了上述算法的高效实现方法，这些实现方法heavily依赖于快速傅里叶变换（FFT）。最后，通过仿真与实验示例验证了所提算法在单比特汽车雷达系统中用于距离‐多普勒成像的有效性。

索引术语 —一位采样，时变阈值，汽车雷达，距离‐多普勒成像，无超参数稀疏参数估计，单比特数据加权SPICE。

I. 引言

MILLIMETER波雷达广泛应用于高级驾驶辅助汽车系统和完全自动驾驶车辆[1]。与其他传感系统（如摄像头、激光雷达和超声波）相比，雷达系统能够提供更优的性能，尤其是在光照不良或恶劣天气条件[2]下。

现有商用汽车雷达系统中最常用的探测波形是LFMCW波形，该波形通过在雷达接收机处使用低速率模数转换器降低了系统成本。线性调频连续波雷达系统发射一系列线性调频信号，这些信号被目标反射并在接收机处与发射的线性调频脉冲混合。距离或距离‐多普勒估计问题被转化为一维或二维复正弦信号参数估计问题[3, 4]。然而，随着线性调频连续波汽车雷达系统的广泛应用，由于它们占据相同的77‐81 GHz频段，相互之间的干扰变得更加严重。相位调制连续波波形可用于缓解干扰问题。为了降低成本，已为PMCW汽车雷达设计了具有理想自相关和互相关特性的二进制序列（例如，参见[5]及其中的参考文献）。二进制序列提供的灵活性和多样性使得PMCW雷达能够像码分多址通信系统一样缓解相互干扰[6]。此外，在编码域中可实现近似正交性，这对多输入多输出操作有利[7, 8]。

为了提高汽车雷达的距离分辨率，基本方法是增加发射信号的带宽，但这会增加模数转换器的成本和功耗。例如，PMCW雷达通常在数字域中进行解调[9]。码片速率为2 GHz的PMCW雷达需要至少2 GHz的采样率[10]。然而，具有高精度量化和高采样率的模数转换器既昂贵又耗电。而低成本和低功耗对于汽车雷达等商用雷达系统至关重要。

一位采样是一种有前景的技术，因其低成本和低功耗的优势，可缓解上述模数转换器问题。由于这些吸引人的特性，一位采样已被应用于雷达感知[11, 12],频谱估计[13–15],以及大规模多输入多输出通信[16–18]。传统一位采样（例如在[19–21],中考虑的）将原始信号与零阈值进行比较，导致信号幅度信息丢失。最近，研究人员已考虑在一位采样中使用时变阈值以实现精确的幅度估计[15, 22]。在这种情况下，通过将接收信号与已知的时变阈值进行比较，获得符号测量。

本文考虑采用具有时变阈值的一位采样技术用于汽车雷达，以降低成本和功耗。我们将一比特距离‐多普勒估计问题建模为一比特稀疏参数估计问题。利用高精度数据进行稀疏参数估计在过去二十年中受到了广泛关注，已开发出多种算法，旨在获得精确的稀疏参数估计。其中，统一加权SPICE算法[23],包括SPICE[24], 、LIKES[25], 、SLIM[26]和IAA[27–29],并不

无需调整任何用户参数，因此在实际应用中易于使用。这些算法具有出色的估计性能，特别是具备高分辨率和低旁瓣特性。此外，IAA在各种环境中表现良好，其鲁棒性在最近的一篇综述文章中被评为较高[30]。然而，这些算法连同传统的快速傅里叶变换都无法直接用于解决单比特稀疏参数估计问题。本文首先提出一种正则化最小化算法，称为1bSLIM，用于基于单比特汽车雷达的精确距离‐多普勒成像。此外，我们指出，通过极大化‐极小化方法[31–35],设计的1bSLIM可被解释为将传统SLIM算法应用于某种修改后的高精度数据。受此关系启发，我们阐述了如何将SPICE、LIKES和IAA推广到单比特情况，并将这些扩展分别称为1bSPICE、1bLIKES和1bIAA。本文提出的每种算法都有其独特优势，可能在特定应用中更受青睐。类似于统一了SPICE、LIKES、SLIM和IAA的原始加权SPICE算法，上述单比特算法也被统一在一比特加权SPICE框架之下。此外，这四种单比特算法均为无需超参数的，因此在实践中易于使用。最后，提供了仿真与实验示例，以验证所提算法在单比特汽车雷达距离‐多普勒成像中的有效性。

符号说明 ：我们分别用粗体小写字母和大写字母表示向量和矩阵。(·)T 和(·)H 分别表示转置和共轭转置。R ∈R N×M 或 R ∈ CN×M 表示一个实值或复值 N × M 矩阵 R。 ⊗ 表示克罗内克积。vec(·)表示按列向量化操作，diag(d)表示由 d构成对角元素的对角矩阵。 ‖ · ‖ 和 ‖ · ‖F 分别表示向量和矩阵的`2 范数和弗罗贝尼乌斯范数。tr{R} 和 |R|分别表示方阵 R的迹和行列式。 A B 表示 B−A 是一个半正定矩阵。Re[x] 和Im[x] 分别表示 x的实部和虚部。 x mod N是x 除以 N的欧几里得除法的余数。最后， j=√−1。

本文中，我们使用以下缩写：
- ADC模数转换器
- AGC 自动增益控制
- CDMA 码分多址
- CGLS 共轭梯度最小二乘
- CPI 相干处理间隔
- DAC 数模转换器
- DFT 离散傅里叶变换
- FFT 快速傅里叶变换
- IAA 迭代自适应方法
- LIKES 基于似然的稀疏参数估计
- 线性调频连续波 线性调频连续波
- 线性最小均方误差 线性最小均方误差
- MAP 最大后验
- MIMO 多输入多输出
- MM 极大化‐极小化
- NMSE 归一化均方误差
- PMCW 相位调制连续波
- PRI 脉冲重复间隔
- SLIM 通过迭代最小化实现稀疏学习
- SPICE 稀疏迭代协方差估计
- SNR 信噪比

II. 问题表述

在本节中，我们首先简要描述线性调频连续波和PMCW雷达的信号模型。然后，利用通过时变阈值进行符号采样获得的符号测量，将距离‐多普勒成像问题建模为稀疏参数估计问题。

A. 线性调频连续波雷达

不失一般性，我们考虑一个线性调频连续波单输入单输出雷达。去斜率和预处理后接收信号的简化模型如下（例如见[11]）：

$$
y(n_1, n_2)=
\sum_{k_d=1}^{K_d}
\sum_{k_r=1}^{K_r}
\gamma_{k_r,k_d} e^{j(\omega_{k_r}n_1+\bar{\omega}_{k_d}n_2)}+e(n_1, n_2),
\quad (1)
$$

其中， $K_r$和 $K_d$分别为距离和多普勒域中的网格点数量；快时间索引$n_1$, $n_1= 1, 2,…, N_1$对应线性调频脉冲内的第$n_1$个采样点；慢时间索引 $n_2$, $n_2= 1, 2,…, N_2$对应第 $n_2$个线性调频脉冲；$\gamma_{k_r,k_d}$表示对应于频率对$(\omega_{k_r},\bar{\omega} {k_d})$的散射体的反射系数；而$e(n_1, n_2)$为未知的加性噪声。频率对$(\omega {k_r},\bar{\omega} {k_d})$通过以下方程与距离‐多普勒对$(R {k_r} , v_{k_d})$近似相关：

$$
\omega_{k_r} = 2\pi\left(\frac{4\mu R_{k_r}}{c f_s} + \frac{2f_0 v_{k_d}}{c f_s}\right),
\quad
\bar{\omega} {k_d} = \frac{4\pi f_0 v {k_d} T_c}{c},
\quad (2)
$$

其中 $2\mu$是调频率； $c$是光速； $f_s$是采样频率； $f_0$表示载波频率；而 $T_c$是脉冲持续时间。因此，可以通过公式(2)从频率对$(\omega_{k_r},\bar{\omega} {k_d})$中恢复距离‐多普勒信息。与线性调频连续波雷达的公式(1)相关的距离‐多普勒估计问题等价于一个二维复值正弦参数估计问题。令测量向量表示为$y=[y(1, 1) y(2, 1)…, y(N_1, N_2)]^T$，并令 $e$表示未知的噪声向量。令未知参数向量表示为$\gamma=[\gamma {1,1}, \gamma_{2,1},…,\gamma_{K_r,K_d}]^T$。公式(1)可重新表述为：

$$
y= B\gamma+ e \in \mathbb{C}^N, \quad B \in \mathbb{C}^{N\times M}, M\gg N, \quad (3)
$$

其中$N= N_1 N_2$和$M= K_r K_d$。 $K_r \ll N_1$和$K_d \ll N_2$是稀疏参数估计算法中常用的假设，用于构建足够精细的网格，使我们能够在真实目标频率不在网格点上时仍获得高分辨率谱估计和优异的结果。令$\psi_N(\omega)=[1, e^{j \omega },…, e^{j( N - 1 ) \omega }]^T$。则$B$的列由${\psi_{N_1,N_2} (\omega_{k_r}, \bar{\omega} {k_d} )} {k_r=1,k_d=1}^{K_r,K_d}$给出，其中$\psi_{N_1,N_2}( \omega_{k_r}, \bar{\omega} {k_d} )=\psi {N_2} (\bar{\omega} {k_d} )\otimes\psi {N_1} (\omega_{k_r} )$。

在雷达距离‐多普勒成像应用中，场景中感兴趣的潜在散射体数量通常远小于网格点的数量，这意味着 $\gamma$中的大多数元素将为零。因此，式(3)中的线性调频连续波雷达距离‐多普勒成像问题可以视为一个稀疏参数估计问题。

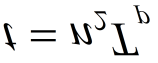
B. PMCW雷达

PMCW雷达周期性地发射一个二进制序列$s=[s(0) s(1)…, s(N_1 − 1)]^T$，其中 $N_1$为序列长度，且 $s$的每个元素为1或 −1，即 $s(n_1) \in{1,−1}$。然后，发射的基带信号可表示为：

$$
x(t)=
\sum_{n_2=-\infty}^{\infty}
\sum_{n_1=0}^{N_1-1}
s(n_1)p(t − n_1T_s − n_2T_p), \quad (4)
$$

其中， $T_s$ 是所谓的码片持续时间； $T_p= N_1T_s$ 是脉冲重复间隔（PRI）； $p(t)$是脉冲成形滤波器的冲激响应，不失一般性地选择为滚降因子为0.25的升余弦函数。为了便于后续信号处理，假设脉冲成形滤波器在区间$(−5T_s, 5T_s]$内非零。设相干处理间隔（CPI）内的距离和多普勒域分别被划分为$K_r$和$K_d$个网格点。然后，在接收机处，我们有：

$$
y(t)=
\sum_{k_r=1}^{K_r}
\sum_{k_d=1}^{K_d}
\gamma_{k_r,k_d} x(t − \tau_{k_r}) e^{j2\pi f_{k_d} t}+ e(t), \quad (5)
$$

其中$\tau_{k_r}$、 $f_{k_d}$ 和$\gamma_{k_r,k_d}$分别表示往返时间延迟、多普勒频率以及对应的反射系数； $e(t)$为未知的加性噪声。对于实值时间延迟 $\tau_{k_r}$，可将其分解为整数部分和小数部分，即$\tau_{k_r} = l_{k_r} T_s+ \bar{\tau} {k_r}$，其中$l {k_r} = \lfloor\tau_{k_r} /T_s\rfloor$， $\lfloor·\rfloor$为向下取整操作。注意，具有时间延迟 $\tau_{k_r} = l_{k_r} T_s+\bar{\tau} {k_r}$ 的回波序列将发射序列循环移位 $l {k_r}$ 个位置，如图1所示。第 $n_2$个周期（即 $n_2T_p \leq t<(n_2+ 1)T_p$）具有实值时间延迟 $\tau_{k_r}$ 的回波信号可表示为：

$$
x(t − \tau_{k_r}) =
\sum_{i=-5}^{N_1+4} s((N_1 + i − l_{k_r}) \mod N_1)
\cdot p(t − n_2 T_p − iT_s − \bar{\tau}_{k_r}). \quad (6)
$$

我们假设在一个相干处理间隔内有 $N_2$个周期，且一个周期内的多普勒频移非常小，可以忽略不计[9, 10]。那么，第$n_2$个周期的接收基带信号可表示为：

$$
y_{n_2} (t)= \sum_{k_r,k_d}
\sum_{i=−5}^{N_1+4}
\gamma_{k_r,k_d} s((N_1+ i − l_{k_r}) \mod N_1)
\cdot p(t − n_2 T_p − iT_s − \bar{\tau} {k_r}) e^{j \bar{\omega} {k_d} n_2}+ e(t), \quad (7)
$$

其中$\bar{\omega} {k_d}= 2\pi f {k_d}T_p$。我们将$t= n_2T_p+ n_1T_s$代入(7)并定义：

$$
\bar{s}(n_1, \tau_{k_r}), x(n_2T_p+ n_1T_s − \tau_{k_r})
=
\sum_{i=-5}^{4}
s((N_1+ n_1+ i − l_{k_r}) \mod N_1) \cdot p(iT_s+ \bar{\tau}_{k_r}).
\quad (8)
$$

注意$p(iT_s)= 0, i \neq 0$。如果$\bar{\tau} {k_r}$等于0，则$\bar{s}(n_1, \tau {k_r})$变为$s((N_1+ n_1 − l_{k_r})\mod N_1)$。接下来，假设在时刻$n_2T_p, …, y_{n_2} = [y(n_2T_p)… y(n_2T_p+ (N_1 − 1)T_s)]^T$处采集了$N_1$个采样点，并令$(y_{n_2}, n_2T_p+(N_1 − 1)T_s)$。那么，可以写成：

$$
y_{n_2}= S\Gamma\phi_{n_2}+ e_{n_2}, \quad (9)
$$

其中反射系数矩阵 $\Gamma$和导向矢量 $\phi_{n_2}$由以下给出：

$$
\Gamma= \begin{bmatrix}
\gamma_{1,1} & \gamma_{1,2} & \dots & \gamma_{1,K_d} \
\gamma_{2,1} & \gamma_{2,2} & \dots & \gamma_{2,K_d} \
\vdots & \vdots & \ddots & \vdots \
\gamma_{K_r,1} & \gamma_{K_r,2} & \dots & \gamma_{K_r,K_d}
\end{bmatrix} \in \mathbb{C}^{K_r\times K_d}, \quad (10)
$$

$$
\phi_{n_2} =[e^{j \bar{\omega} 1n_2}, e^{j \bar{\omega}_2n_2},…, e^{j \bar{\omega} {K_d} n_2}]^T, \quad (11)
$$

且 $S \in \mathbb{R}^{N_1\times K_r}$定义为：

$$
S= \begin{bmatrix}
\bar{s}(0, \tau_1) & \bar{s}(0, \tau_2) & \dots & \bar{s}(0, \tau_{K_r}) \
\bar{s}(1, \tau_1) & \bar{s}(1, \tau_2) & \dots & \bar{s}(1, \tau_{K_r}) \
\vdots & \vdots & \ddots & \vdots \
\bar{s}(N_1 − 1, \tau_1) & \bar{s}(N_1 − 1, \tau_2) & \dots & \bar{s}(N_1 − 1, \tau_{K_r})
\end{bmatrix}.
\quad (12)
$$

令

$$
Y=[y_0, y_1,…, y_{N_2 −1}], \quad (13)
$$

$$
\Phi=[\phi_1,\phi_2,…,\phi_{N_2}]^T, \quad (14)
$$

$$
E=[e_1, e_2,…, e_{N_2}] . \quad (15)
$$

然后，观测数据矩阵可以简洁地表示如下：

$$
Y= S\Gamma\Phi^T + E. \quad (16)
$$

令$\gamma= \text{vec}(\Gamma)$， $y= \text{vec}(Y)$和$e= \text{vec}(E)$。则(16)中的数据模型可重写为：

$$
y= B\gamma+ e \in \mathbb{C}^N, \quad B \in \mathbb{C}^{N\times M}, M\gg N, \quad (17)
$$

其中 $B= \Phi \otimes S$已知， $N= N_1N_2$和 $M= K_rK_d$。与线性调频连续波雷达情况类似，PMCW雷达的距离‐多普勒成像问题也可以视为一个稀疏参数估计问题，其未知参数向量 $\gamma$是稀疏的。

C. 单比特量化

在LFMCW和PMCW雷达的接收机处应用单比特量化，通过将未量化的接收信号 $y$与已知的时变阈值 $h, h_R + jh_I$进行比较，得到符号测量向量 $z= z_R + jz_I$：

$$
z= \text{sign}_c(B\gamma −h+ e), \quad (18)
$$

其中$\text{sign}_c(x)= \text{sign}(\text{Re}[x])+ j\text{sign}(\text{Im}[x])$且

$$
\text{sign}(x)=
\begin{cases}
1 & x> 0, \
-1 & x< 0.
\end{cases}
\quad (19)
$$

感兴趣的问题是，在给定符号测量向量 $z$的情况下，对 $\gamma$找到一个精确的稀疏估计。在接下来的章节中，我们将介绍几种用于单比特汽车雷达距离‐多普勒成像问题的求解方法。

III. 加权SPICE框架概述

我们首先回顾一下针对标准高精度数据模型（3）或（17）的SPICE算法。为了迭代求解与SPICE相关的优化问题，文献[24]中采用了循环方法，而文献[23]中使用了梯度方法。我们表明，可以利用MM方法推导出相同的加权SPICEa算法[23]。在将加权SPICE算法扩展到一位数据情况时，后续需要用到其MM推导过程。此外，我们在附录A中简要回顾了MM的基本思想。

为了记号方便，我们用${\gamma_k}$表示(3)或(17)中向量 $\gamma$的元素。SPICE算法假设

$$
\mathbb{E}[ee^H]= \begin{bmatrix}
p_{M+1} & 0 & \dots & 0 \
0 & p_{M+2} & \dots & 0 \
\vdots & \vdots & \ddots & \vdots \
0 & \dots & \dots & p_{M+N}
\end{bmatrix}, \quad (20)
$$

且${\gamma_k}$的相位在$[0, 2\pi]$上独立均匀分布（参见[24]中的讨论，表明这些假设对算法性能的影响微乎其微）。那么，数据向量 $y$的协方差矩阵具有以下形式：

$$
R= \mathbb{E}{yy^H}= BP_1B^H+ P_2
= AP^H, \quad (21)
$$

其中$P_1 =\text{diag}(p_1), p_1 =[p_1 ,…, p_M]^T$；$P_2 = \text{diag}(p_2), p_2 =[p_{M+1} ,…, p_{M+N}]^T$；并且其中$A=[B I], P= \text{diag}(p), p=[p_1^T p_2^T]^T$. (22)

供后续使用，设 $A=[a_1, a_2,…, a_{M+N}]$。

A. SPICE

SPICE最小化以下协方差拟合准则[24]：

$$
\min_p |R^{-1/2} (yy^H − R)|^2_F . \quad (23)
$$

经过简单计算，SPICE准则可以重新表述为[23]：

$$
\min_p f_1(p)= y^H R^{-1} y+ \text{tr}{R}
= y^H R^{-1} y+ \sum_{k=1}^{M+N} w_kp_k , \quad (24)
$$

其中 $w_k= |a_k|^2$。尽管最小化(24)的优化问题是一个凸半定规划(SDP)，但使用通用SDP求解器将会是计算密集型的[24]。利用MM技术，可以通过每次迭代具有闭式解的方式高效地迭代求解(24)中的优化问题。以下不等式为 $R^{-1}$提供了上界：

$$
R^{-1} \preceq(\hat{R}_t)^{-1}A\hat{P}_tP^{-1} \hat{P}_tA^H(\hat{R}_t)^{-1}, \quad (25)
$$

其中，$\hat{P}_t$和$\hat{R}_t= A\hat{P}_tA^H$表示$P$和$R$在第$t$次迭代时的估计；且等式在$P=\hat{P}_t$处成立。虽然该性质由[36],推出，但为了使本文自成体系，我们在附录B中给出了一个简单的证明。利用(25)，我们可以得到$f_1(p)$的一个优函数如下：

$$
f_1(p) \leq g_1(p|\hat{p} t)=(\bar{\gamma}^{(t+1)})^HP^{-1}\bar{\gamma}^{(t+1)}+ \sum {k=1}^{M+N} w_kp_k, \quad (26)
$$

其中

$$
\bar{\gamma}^{(t+1)}= \hat{P} t A^H(\hat{R}_t)^{-1}y
,[(\hat{\gamma}^{(t+1)})^T, \bar{\gamma}^{(t+1)} {M+1},…,\bar{\gamma}^{(t+1)}_{M+N}]^T. \quad (27)
$$

注意，$\hat{\gamma}^{(t+1)}=\hat{P}_t^1B^H(\hat{R}_t)^{-1}y$是对应于估计值$\hat{p}_t^1$[23, 37]的 $\gamma$的LMMSE估计。优函数 $g_1(p|\hat{p}_t)$易于最小化，因为

$$
g_1(p|\hat{p} t)= \sum {k=1}^{M+N} \frac{|\bar{\gamma}^{(t+1)}_k|^2}{p_k} + w_kp_k

\sum_{k=1}^{M+N} 2\sqrt{w_k} |\bar{\gamma}^{(t+1)}_k| , \quad (28)
$$

等式在以下情况下成立

$$
\hat{p}^{(t+1)}_k = |\bar{\gamma}^{(t+1)}_k| /\sqrt{w_k}.
\quad (29)
$$

将 $\bar{\gamma}^{(t+1)}_k$代入(29)得：

$$
\hat{p}^{(t+1)}_k = \hat{p}^t_k |\ a^H_k(\hat{R}_t)^{-1} y| /w^{1/2}_k.
\quad (30)
$$

给定$\hat{p}^{(t+1)}$，SPICE通过$\hat{R}^{(t+1)} = A\hat{P}^{(t+1)}A^H$更新协方差矩阵。尽管推导方式不同，(30)中的更新方案与[23]中SPICEa算法的更新方案一致。由于优化问题的凸性和MM技术的单调递减性质，该算法的全局收敛性得以保证。

一旦获得$\hat{p}$，我们可以通过著名的LMMSE估计器来估计 $\gamma$：

$$
\hat{\gamma}= \hat{P}_1 B^H \hat{R}^{-1} y. \quad (31)
$$

B. LIKES

LIKES通过最小化负对数似然函数来估计 $p$：

$$
f_2(p)= y^H R^{-1} y+ \ln|R| . \quad (32)
$$

注意，$\ln|R|$是 $p$的凹函数，因此(32)的最小化是一个困难的非凸优化问题。我们再次使用MM技术在每次迭代中高效地降低(32)。通过一阶泰勒展开，可以很容易地为$\ln|R|$构造一个优函数：

$$
\ln|R| \leq \sum_{k=1}^{M+N}(a^H_k(\hat{R}_t)^{-1}a_k)p_k+ \text{const}. \quad (33)
$$

使用(33)可得到 $f_2(p)$的以下优函数：

$$
f_2(p) \leq g_2(p|\hat{p} t)= y^HR^{-1}y+ \sum {k=1}^{M+N} w_kp_k, \quad (34)
$$

with

$$
w_k= a^H_k(\hat{R}_t)^{-1}a_k. \quad (35)
$$

与SPICE算法的固定权重不同，LIKES的权重在极大化‐极小化迭代过程中被更新。对于在$(t+ 1)$次迭代时固定的权重，优函数 $g_2(p|\hat{p}_t)$具有与SPICE准则相同的形式（见(24)）。因此，可以通过上一小节中提出的SPICE求解器来实现对 $g_2(p|\hat{p}_t)$的减小或最小化。LIKES包含内层和外层迭代。在第$(t+1)$次外层迭代时，

$$
\hat{p}^{(t+1)} {l+1,k}= \hat{p}^{(t+1)} {l,k} \frac{| a^H_k(\hat{R}^{(t+1)}_l)^{-1} y |}{(a^H_k(\hat{R}_t)^{-1}a_k)^{1/2}}, \quad l= 0,…, L− 1, \quad (36)
$$

其中，$\hat{p}^{(t+1)} {l,k}$,和$\hat{R}^{(t+1)} {l}$分别表示在第 $l$次内层迭代和第$(t+ 1)$次外层迭代时 $p_k$和 $R$的估计值，且有$\hat{p}^{(t+1)} {0,k}= \hat{p}^t_k$以及$\hat{R}^{(t+1)} {0}= \hat{R} t$； $L$表示内层迭代次数。在实际应用中， $L$可以是一个较小的数，甚至为1。经过 $L$次内层迭代后，我们令$\hat{p}^{(t+1)}_k = \hat{p}^{(t+1)} {L,k}$,和$\hat{R}^{(t+1)} = \hat{R}^{(t+1)}_{L}$，并根据(35)更新权重${w_k}$，然后继续下一次外层迭代。

LIKES具有局部收敛性，但由于(32)是关于 $p$的非凸函数，因此该算法的全局收敛性难以分析。

C. SLIM

通过采用LIKES稀疏性强制项的一种略微不同的形式，SLIM所优化的准则具有以下形式：

$$
f_3(p)= y^H R^{-1} y+ \ln|P| . \quad (37)
$$

再次，$\ln |P|$是$p$的凹函数，并且可以通过一阶泰勒展开构造一个优函数：

$$
\ln|P| = \sum_{k=1}^{M+N} \ln|p_k| \leq \sum_{k=1}^{M+N} \frac{p_k}{\hat{p}^t_k} + \text{const}. \quad (38)
$$

利用(25)和(38)，可得到 $f_3(p)$的如下优函数：

$$
f_3(p) \leq g_3(p|\hat{p} t )=(\bar{\gamma}^{(t+1)})^H P^{-1} \bar{\gamma}^{(t+1)}+ \sum {k=1}^{M+N} w_kp_k,
\quad (39)
$$

其中$w_k= 1/\hat{p}^t_k$。最小化$g_3(p|\hat{p}_t)$可得SLIM的第$(t+ 1)$个更新公式：

$$
\hat{p}^{(t+1)}_k=(\hat{p}^t_k)^{3/2} |a^H(R_t)^{-1}y|. \quad (40)
$$

与LIKES类似，SLIM单调地减小(37)中的目标函数，并局部收敛。

D. IAA

目前尚无已知的基于目标函数推导的IAA方法，类似于上述的(24)、(32)或(37)。根据该算法在[27, 28],中的近似解释，IAA的权重由以下给出：

$$
w_k= \hat{p}^t_k(a^H_k(\hat{R}_t)^{-1}a_k)^2. \quad (41)
$$

将(41)代入(30)得到IAA更新公式：

$$
\hat{p}^{(t+1)}_k=(\hat{p}^t_k)^{1/2} \frac{| a^H_k(\hat{R}_t)^{-1}y |}{a^H_k(\hat{R}_t)^{-1}a_k}. \quad (42)
$$

上述四种算法都可以统一在加权SPICE框架下（如上所述，IAA只能近似地纳入该框架）：

$$
\min_p y^H R^{-1}y+ \sum_{k=1}^{M+N} w_kp_k. \quad (43)
$$

(24)、(35)、(39)和(41)中权重${w_k}$的不同选择导致了四种不同的无超参数算法。SPICE具有固定权重，而LIKES、SLIM和IAA使用自适应权重，可被解释为自适应重加权SPICE方法。

IV. 一比特SLIM

在本节中，我们提出了一种用于单比特情况的正则化最小化方法，称为1bSLIM。经过单比特量化后，线性模型(3)或(17)变为非线性模型(18)。该问题的目标是从单比特量化信号 $z$中估计 $\gamma$，并利用已知的时变阈值 $h$这一事实。

假设 $e$是独立同分布的零均值、方差未知的圆对称复值高
斯白噪声$\sigma^2$，即$\text{Re}[e(n)] \sim \mathcal{N}(0, \sigma^2)$和$\text{Im}[e(n)] \sim \mathcal{N}(0, \sigma^2)$[22, 38]：

$$
L(\gamma, \sigma)= -\sum_{n=1}^{N} \ln \left(\Phi \left(\frac{z_R(n)(\text{Re}[b_n^T \gamma] - h_R(n))}{\sigma/\sqrt{2}}\right)\right)
-\sum_{n=1}^{N} \ln \left(\Phi \left(\frac{z_I(n)(\text{Im}[b_n^T \gamma] - h_I(n))}{\sigma/\sqrt{2}}\right)\right), \quad (44)
$$

其中$\Phi(x)= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-t^2/2} dt$是标准高斯分布的累积密度函数，且$b_n$是$B^T$的第$n$列。为方便起见，我们通过对$\eta= \sqrt{2}/\sigma$和$\beta= \eta\gamma$进行定义。然后，(44)可以重新表述为：

$$
L(\beta, \eta)= -\sum_{n=1}^N \ln(\Phi(z_R(n)(\text{Re}[b_n^T\beta] - \eta h_R(n))))
-\sum_{n=1}^N \ln(\Phi(z_I(n)(\text{Im}[b_n^T\beta] - \eta h_I(n)))), \quad (45)
$$

考虑最小化以下用于稀疏参数估计的正则化负对数似然函数：

$$
G(\beta, \eta)= L(\beta, \eta)+ \sum_{k=1}^{M} \ln(|\beta_k|^2+ \varepsilon), \quad (46)
$$

其中 $\varepsilon> 0$是一个很小的正数，用于确保该函数具有有限的下界。 $G(\beta, \eta)$的第一项（即 $L(\beta, \eta)$）为拟合项，第二项（即$\sum_{k=1}^M \ln(|\beta_k|^2+ \varepsilon)$）为稀疏性强制项。与原始SLIM算法类似，1bSLIM可被解释为一种最大后验方法。

考虑以下贝叶斯模型：

$$
p(z|\beta, \eta)= \prod_{n=1}^{N} \Phi(z_R(n)(\text{Re}[b_n^T\beta] - \eta h_R(n))) \Phi(z_I(n)(\text{Im}[b_n^T\beta] - \eta h_I(n))),
\quad
p(\beta) \propto \prod_{k=1}^{M} \frac{1}{|\beta_k|^2+ \varepsilon}, \quad p(\eta) \propto 1, \quad (47)
$$

其中$p(\beta) \propto \prod_{k=1}^{M} \frac{1}{|\beta_k|^2+ \varepsilon}$是非信息性先验[39]。我们可以通过最大后验方法估计$\beta$和$\eta$：

$$
(\hat{\beta}, \hat{\eta})= \arg \max_{\beta,\eta} p(z|\beta, \eta)p(\beta)p(\eta). \quad (48)
$$

注意，在对上述表达式取负对数后，(48)等价于(46)。

为了高效地最小化(46)中的复杂且非凸的目标函数，我们再次采用MM方法。具体而言，我们首先为$L(\beta, \eta)$推导出一个优函数。随后，获得每次MM迭代的闭式更新公式。

A. $L(\beta, \eta)$的优函数

令$f(x)= -\ln(\Phi(x))$。对于任意$u, x \in \mathbb{R}$[22]，以下不等式成立：

$$
f(x) \leq f(u)+ f’(u)(x - u)+ \frac{1}{2}(x - u)^2. \quad (49)
$$

令

$$
x_R(n)= z_R(n)(\text{Re}[b_n^T \beta] - \eta h_R(n)), \quad x_I(n)= z_I(n)(\text{Im}[b_n^T \beta] - \eta h_I(n)),
\quad
f’(x)= -\frac{\varphi(x)}{\Phi(x)},
$$

其中$\varphi(x)= \frac{1}{\sqrt{2\pi}} e^{-x^2/2}$是标准正态概率密度函数。然后，负对数似然函数(45)中的$L(\beta, \eta)$可以写成：

$$
L(\beta, \eta)= \sum_{n=1}^N f(x_R(n))+ \sum_{n=1}^N f(x_I(n)). \quad (50)
$$

假设从第 $t$次迭代中已获得$\hat{\beta}_t$和$\hat{\eta}_t$，我们可利用(49)得到 $L(\beta, \eta)$的一个优函数：

$$
L(\beta, \eta) \leq \sum_{n=1}^{N} \frac{1}{2} x_R^2(n)+ \frac{1}{2} x_I^2(n)
- u_{t,R}(n)x_R(n)- u_{t,I}(n)x_I(n)+ \text{const}, \quad (51)
$$

其中 $u_{t,R/I}(n)$由下式给出：

$$
u_{t,R/I}(n)= x_{t,R/I}(n)- f’(x_{t,R/I}(n)). \quad (52)
$$

简单的计算表明，(51)可以重写为如下形式：

$$
L(\beta, \eta) \leq \frac{1}{2}|B\beta -( \eta h+ g_t)|^2+ \text{const}, \quad (53)
$$

其中$g_t=[g_t(1)…, g_t(N)]^T$，其中

$$
g_t(n)= z_R(n)u_{t,R}(n)+ jz_I(n)u_{t,I}(n). \quad (54)
$$

B. 更新公式

利用(53)和(38)，并忽略与$\beta$和$\eta$无关的项，可得到目标函数 $G(\beta, \eta)$在第$(t+1)$次迭代处的以下优函数：

$$
Q(\beta, \eta|\hat{\beta}_t, \hat{\eta}_t)= \frac{1}{2} |B\beta -( \eta h+ g_t)|^2+ \beta^H(\hat{P}_t)^{-1} \beta, \quad (55)
$$

其中 $\hat{P} t= \text{diag}{\hat{p}_t}$ with $\hat{p}_t=[\hat{p} {t,1}, \hat{p} {t,2},…,\hat{p} {t,M}]$ and

$$
\hat{p} {t,k}= |\hat{\beta} {t,k}|^2+ \varepsilon. \quad (56)
$$

请注意，关于$\beta$和$\eta$最小化 $Q(\beta, \eta|\hat{\beta}_t, \hat{\eta}_t)$是一个无约束二次优化问题，我们可以通过将复导数$(d/d\beta^H) Q(\beta, \eta|\hat{\beta}_t, \hat{\eta}_t)$和$(d/d\eta) Q(\beta, \eta|\hat{\beta}_t, \hat{\eta}_t)$设为零来求得$\hat{\beta}^{(t+1)}$和$\hat{\eta}^{(t+1)}$（暂时忽略 $\eta> 0$的事实）。该方法导出了以下线性方程：

$$
(B^H B+2(\hat{P}_t)^{-1})\beta - \eta B^H h= B^H g_t, \quad (57)
$$

$$
-\text{Re}[h^H B\beta]+ \eta h^H h= -\text{Re}[h^H g_t]. \quad (58)
$$

由于矩阵 $B^H B+ 2(\hat{P}_t)^{-1}$是正定的，我们可以从方程(57)得到$\beta$如下：

$$
\beta=[B^H B+2(\hat{P}_t)^{-1}]^{-1} B^H (\eta h+ g_t), = \hat{P}_t B^H (\hat{R}_t)^{-1} (\eta h+ g_t), \quad (59)
$$

其中

$$
\hat{R}_t = B \hat{P}_t B^H +2I. \quad (60)
$$

将(59)中的$\beta$代入(58)，我们得到$\hat{\eta}^{(t+1)}$的解：

$$
\hat{\eta}^{(t+1)}= \max \left(0,- \frac{\text{Re}[h^H(\hat{R}_t)^{-1}g_t]}{h^H(\hat{R}_t)^{-1}h} \right). \quad (61)
$$

最后，将$\hat{\eta}^{(t+1)}$代入(59)式可得：

$$
\hat{\beta}^{(t+1)}= \hat{P}_t B^H(\hat{R}_t)^{-1}(\hat{\eta}^{(t+1)}h+ g_t). \quad (62)
$$

通过使用MM技术，我们之前推导出的优函数(55)比原始目标函数(46)更容易最小化。由于采用MM方法论推导该算法，目标函数$G(\beta, \eta)$可保证单调递减，因此1bSLIM收敛到(46)式代价函数的局部最小值。

V. 一比特加权SPICE框架

在本节中，我们首先讨论了所提出的用于一位数据的1bSLIM与用于高精度数据的原始SLIM算法之间的关系。通过使用MM方法，1bSLIM的每一次迭代均可被解释为对修改后的高精度数据应用原始SLIM的一个步骤，并且具有与原始SLIM类似的更新公式。受此联系以及加权SPICE算法的MM推导的启发，我们还将SPICE、LIKES和IAA推广到单比特数据情况。

A. 1bSLIM与SLIM之间的联系

考虑以下代价函数：

$$
\bar{G}(\beta, p, \eta)= L(\beta, \eta)+ \sum_{k=1}^{M} \frac{|\beta_k|^2}{p_k}+ \sum_{k=1}^{M} \ln(p_k+ \varepsilon). \quad (63)
$$

注意，关于 $p$（对于 $\varepsilon= 0$）最小化 $\bar{G}(\beta, p, \eta)$可得$p_k= |\beta_k|^2$，因此(63)可简化为(46)。这一事实表明，(63)是(46)的增广形式，因此可通过关于$\beta$和$\eta$最小化(46)来方便地实现对(63)的最小化。

在本节中，我们使用(63)来讨论1bSLIM与SLIM之间的联系。利用不等式(38)和(53)，并忽略与$\beta$、 $p$和$\eta$无关的项，可得到目标函数$\bar{G}(\beta, p, \eta)$的如下优函数：

$$
\bar{Q}(\beta, p, \eta)= \frac{1}{2} |B\beta-(\eta h+ g_t)|^2 +\beta^H P^{-1} \beta+ \sum_{k=1}^{M} w_kp_k, \quad (64)
$$

其中

$$
P= \text{diag}{p} \quad \text{and} \quad w_k = 1/(\hat{p}_{t,k} + \varepsilon). \quad (65)
$$

令

$$
\bar{y}^{(t+1)}= \hat{\eta}^{(t+1)}h+ g_t. \quad (66)
$$

然后，$\bar{Q}(\beta, p, \hat{\eta}^{(t+1)})$变为

$$
\bar{Q}(\beta, p, \hat{\eta}^{(t+1)})= \frac{1}{2} |\bar{y}^{(t+1)} -B\beta|^2+ \sum_{k=1}^{M} \frac{|\beta_k |^2}{p_k} + \sum_{k=1}^{M} w_kp_k. \quad (67)
$$

关于$\beta$对$\bar{Q}(\beta, p, \hat{\eta}^{(t+1)})$的最小化得到：

$$
\min_\beta \bar{Q}(\beta, p, \hat{\eta}^{(t+1)})=(\bar{y}^{(t+1)})^H R^{-1}\bar{y}^{(t+1)}+ \sum_{k=1}^{M} w_kp_k, \quad (68)
$$

其中$R= BP B^H+2I$，最小值在以下位置取得：

$$
\beta= P B^H R^{-1}\bar{y}^{(t+1)}. \quad (69)
$$

因此，$\bar{Q}(\beta, p, \hat{\eta}^{(t+1)})$是(68)中加权SPICE准则的增广函数。通过将$\bar{y}^{(t+1)}$视为修正后的高精度数据，(68)中的加权SPICE准则与原始SLIM的准则一致。

总之，通过使用MM技术，可以利用由$\bar{y}^{(t+1)}$给出的高精度数据的线性模型来近似求解（18）中非线性模型的稀疏参数估计问题。

$$
\bar{y}^{(t+1)}= B\beta+ \bar{e}, \quad (70)
$$

其中噪声向量$\bar{e}$的均值和协方差矩阵分别为0和$2I$。然后，1bSLIM的幅度$\beta$和功率$p$可以通过对(70)中的$\bar{y}^{(t+1)}$应用SLIM等效地获得。

B. 将SPICE、LIKES和IAA扩展到单比特情况

第三节表明，加权SPICE算法的四种不同权重选择对应于四种不同的稀疏性强制项，并导致四种不同的无需超参数的稀疏参数估计算法。现在，我们利用SPICE、LIKES和IAA的稀疏性强制项，将这些算法扩展到一比特数据情况。

1) 1bSPICE

将(63)中的稀疏性强制项替换为$\text{tr}{R}$，我们得到以下优化准则：

$$
G_1(\beta, p, \eta)= L(\beta, \eta)+ \sum_{k=1}^{M} \frac{|\beta_k|^2}{p_k}+ \text{tr}{R}. \quad (71)
$$

利用(53)可得到(71)的以下优函数：

$$
\bar{Q} 1(\beta, p, \eta)= \frac{1}{2} |B\beta-(\eta h+ g_t)|^2 +\beta^H P^{-1}\beta+ \sum {k=1}^{M} w_kp_k, \quad (72)
$$

其中$w_k = |b_k|^2$。(72)的最小化可以通过分块循环算法实现，该算法交替地在固定$p$时对${\beta, \eta}$最小化(72)，并在固定${\beta, \eta}$时对$p$最小化(72)。即，通过求解以下子问题迭代地更新${\beta, \eta}$和$p$：

$$
{ \hat{\beta}^{(t+1)}, \hat{\eta}^{(t+1)} }= \arg \min_{\beta,\eta} \bar{Q}_1(\beta, \hat{p}_t, \eta), \quad (73)
$$

$$
\hat{p}^{(t+1)} = \arg \min_{p} \bar{Q}_1(\hat{\beta}^{(t+1)}, p, \hat{\eta}^{(t+1)}). \quad (74)
$$

注意，(73)中的优化问题与(55)中的相似。因此，$\hat{\eta}^{(t+1)}$和$\hat{\beta}^{(t+1)}$的更新公式分别与(61)和(62)中的相似。该优化问题(74)的解为：

$$
\hat{p}^{(t+1)}_k= |\hat{\beta}^{(t+1)}_k|/\sqrt{w_k}. \quad (75)
$$

大量数值示例表明，仅对(73)和(74)迭代一次来减小(72)，通常就能获得与多次迭代这两个方程相似的性能，但总体计算成本更低。由于块状循环算法的单调性性质得以保证，因此

$$
\bar{Q}_1(\hat{\beta}_t, \hat{p}_t, \hat{\eta}_t)> \bar{Q}_1(\hat{\beta}^{(t+1)}, \hat{p}_t, \hat{\eta}^{(t+1)})

\bar{Q}_1(\hat{\beta}^{(t+1)}, \hat{p}^{(t+1)}, \hat{\eta}^{(t+1)}).
$$

第一个不等式来自于对$\bar{Q}_1(\beta, \hat{p}_t, \eta)$关于${\beta, \eta}$的最小化，第二个不等式可以通过减小$\bar{Q}_1(\hat{\beta}^{(t+1)}, p, \hat{\eta}^{(t+1)})$关于$p$来保证。

由于该算法与SPICE算法的关联，我们将上述算法称为1bSPICE。1bSPICE在每次迭代中都会减小(71)，并收敛到一个局部最小值。

2) 1bLIKES

将(63)中的稀疏性强制项替换为$\ln|R|$，我们得到以下准则：

$$
G_2(\beta, p, \eta)= L(\beta, \eta)+ \sum_{k=1}^{M} \frac{|\beta_k|^2}{p_k}+ \ln|R|. \quad (76)
$$

利用(33)和(53)，我们可以得到$G_2(\beta, p, \eta)$的一个优函数，其形式与(72)中的相同（只是(72)中的权重$w_k$采用(35)中的形式）。$\eta, \beta$和$p$的更新公式具有与(61)、(62)和(75)中类似的形式。我们将所得到的算法称为1bLIKES，因为1bLIKES通过(67)和(68)与LIKES算法相关联。

1bLIKES生成一系列估计值，单调地减小(76)，并收敛到该函数的一个局部最小值。根据[23]中的引理1：

$$
b_k^H(\hat{R} t)^{-1}b_k \leq 1/\hat{p} {t,k}, \quad (77)
$$

这意味着1bLIKES的权重小于1bSLIM（对于$\varepsilon= 0$）。因此，1bLIKES将产生稀疏性较低的结果。

3) 1bIAA

最后，将(72)中的权重替换为(41)中的IAA的权重，可得到对应于IAA准则的增广函数，我们将由此得到的算法称为1bIAA。由(77)可知，IAA的权重小于LIKES和SLIM的权重。因此可以推测，1bIAA得到的结果相比1bSLIM和1bLIKES的结果稀疏性较低。1bIAA的更新公式与1bSPICE的更新公式相同，只是将$w_k$替换为(41)中的IAA的权重。尽管我们未能找到1bIAA的优化度量标准，但我们从未遇到过1bIAA不收敛的例子（IAA和1bIAA的收敛性质研究是未来一个有趣的研究课题）。

备注 1 ：1bSPICE、1bLIKES、1bSLIM和1bIAA在$(t+ 1)$次迭代处的优函数具有相同的形式，如(68)所示，但具有不同的权重。因此，这四种算法可以在一位加权SPICE框架下统一。一比特加权SPICE与传统的加权SPICE相关，因为前者等价于在$(t+1)$次迭代时将后者应用于(70)中的修正高精度数据。所提出的一比特加权SPICE框架总结于表I中。

C. 实现方法

1) 初始化与终止

所提出的四种算法使用一些较小的复数值幅度估计进行初始化，例如等于$(1+ j) \times 10^{-3}$。当连续两次迭代之间$p$的相对变化小于$10^{-3}$，或达到最大迭代次数150时，即实现“实际收敛”。(46)中的$\varepsilon$通常选择为一个较小的正数（例如，$\varepsilon= 10^{-4}$）。

2) 1bSLIM和1bSPICE的快速实现

在1bSLIM和1bSPICE的迭代过程中，我们需要根据上一次迭代得到的功率估计值$P$来计算协方差矩阵$R$及其逆矩阵，这一操作具有较高的计算负担。我们可以通过首先使用CGLS方法[26, 40]计算$v_{t,1}=(\hat{R} t)^{-1}h$和$v {t,2}=(\hat{R} t)^{-1}g_t$来降低计算负担。然后，$\hat{\eta}^{(t+1)}= -\max{0, \text{Re}[h^H v {t,2}]/(h^H v_{t,1})}$且$\hat{\beta}^{(t+1)} k=\hat{p} {t,k} b_k^H(\hat{\eta}^{(t+1)}v_{t,1}+ v_{t,2})$。在CGLS的每次迭代中，主要的计算步骤是矩阵‐向量乘积$Bx$（其中$x$是一个长度为$M$的任意向量）。对于FMCW距离‐多普勒成像问题，矩阵‐向量乘积$Bx$可以通过对$x$应用二维逆快速傅里叶变换高效地计算。

3) 1bLIKES和1bIAA的快速实现

在1bLIKES和1bIAA中，协方差矩阵$R$及其逆的计算无法避免。对于PMCW雷达，二维协方差矩阵$R$可以表示为：

$$
R=(\Phi \otimes S)P(\Phi \otimes S)^H = \sum_{k_r=1}^{K_r} \sum_{k_d=1}^{K_d} p_{k_r,k_d}[\phi_{K_d}(k_d)\phi_{K_d}^H(k_d)] \otimes[s_{k_r} s_{k_r}^H], \quad (78)
$$

其中$p_{k_r,k_d}$是范围‐多普勒网格点$(k_r, k_d)$处的功率。由(78)可知，$R$具有块托普利茨结构，包含$K_d \times K_d$个块，每个块具有$K_r \times K_r$个元素：

$$
R= \begin{bmatrix}
R_1 & R_2 & \dots & R_{K_d} \
R_{-2} & R_1 & \dots & R_{K_d -1} \
\vdots & \vdots & \ddots & \vdots \
R_{-K_d} & R_{-K_d +1} & \dots & R_1
\end{bmatrix}. \quad (79)
$$

Gohberg‐Semencul分解可用于通过快速傅里叶变换（FFT）[41, 42]高效计算$R^{-1}$。对于通过线性调频连续波雷达实现的距离‐多普勒成像，二维协方差矩阵$R$具有托普利茨‐块‐托普利茨结构。1bLIKES和1bIAA在线性调频连续波雷达上的快速实现可遵循[29]中提供的步骤。

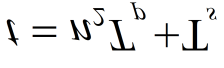
VI. 模拟与实验示例

我们现在通过模拟和实验示例来评估所提出的一位加权SPICE算法的性能。我们首先关注使用线性调频连续波雷达进行测距，然后转向利用PMCW雷达进行距离‐多普勒成像。最后，我们给出了使用一位加权SPICE算法对实测LFMCW雷达数据进行距离‐多普勒成像的实验示例。

所有示例均在配备Intel(R) i5‐8250U @1.60 GHz处理器和8.0 GB内存的PC上运行。

A. 模拟示例

1) 基于线性调频连续波雷达的测距

如第二节A部分所述，使用线性调频连续波雷达进行测距问题对应于一维正弦参数估计问题。我们考虑的长度为$N= 1024$的信号由五个幅度为${\alpha_k} {k=1}^5 ={1, 0.8, 0.8, 0.6, 0.4}$、频率为${0.150 \times2\pi, 0.216\times 2\pi,(0.216+1/N)\times 2\pi, 0.375\times 2\pi, 0.450\times 2\pi}$且相位从区间$[0, 2\pi]$上的均匀分布中独立随机选取的正弦波组成。我们在频域中使用的网格点数量为$M= 5N$。需要注意的是，第二个和第三个正弦波的真实频率并不恰好位于频率网格上，且它们之间的频率间隔等于传统周期图的频率分辨率极限。时变阈值的实部和虚部分别从预定义的八元素集合${-h {\max},-h_{\max} +\Delta,…, h_{\max} -\Delta, h_{\max}}$中随机且等概率选取，其中$h_{\max} = \sqrt{\sum_{k=1}^{5} \alpha_k^2 +\sigma^2}/2$和$\Delta= 2h_{\max}/7$。注意在实际应用中，可通过模拟自动增益控制获得接收信号功率（即$\sum_{k=1}^{5} \alpha_k^2 + \sigma^2$）的粗略估计电路[18]。该阈值用于获取带符号的测量值。信噪比（SNR）定义为$10 \log_{10} (\sum_{k=1}^{5} \alpha_k^2 / \sigma^2)$，设定为20分贝。

在图2(a)中，我们展示了通过一位周期图[43],（称为1bPER）获得的谱估计幅度。1bPER存在明显的泄漏（即高旁瓣）和较差的分辨率问题（无法分辨第二个和第三个正弦信号）。图2(b)显示了使用ADMM对数范数算法[15],（称为ADMM）得到的结果。ADMM的幅度估计通常被高估，并且该算法也存在与1bPER类似的分辨率问题。图2(c)–2(f)中的一位加权SPICE结果显示出更高的分辨率和更低的旁瓣。我们观察到，1bSPICE存在轻微的幅度低估问题，而1bLIKES、1bSLIM和1bIAA提供了准确的幅度估计。与原始加权SPICE算法的行为类似，1bLIKES和1bSLIM的结果比1bIAA更稀疏。

为进一步说明算法的性能，我们在图3(a)和图3(b)中分别展示了500次蒙特卡洛仿真得到的幅度估计的归一化均方误差以及平均旁瓣功率随信噪比的变化情况。平均归一化均方误差和平均旁瓣功率$P_s$的计算公式如下：

$$
\text{NMSE}= \frac{1}{2500} \sum_{k=1}^{5} \sum_{i=1}^{500} \frac{|\hat{\alpha} k^{(i)} - \alpha_k|^2}{\alpha_k^2},
\quad
P_s = \frac{1}{500} \sum {i=1}^{500} \left( |\hat{\gamma}^{(i)}|^2 - \sum_{k=1}^{5} (\hat{\alpha}_k^{(i)})^2 \right),
$$

其中$\hat{\alpha}_k^{(i)}$表示在第$i$次蒙特卡洛运行中对$\alpha_k$的估计值；$\hat{\gamma}^{(i)}$表示在第$i$次蒙特卡洛运行中估计的稀疏参数向量，每次蒙特卡洛运行对应于独立的噪声和阈值实现。检查结果后，我们发现1bPER的幅度估计较差且旁瓣电平较高。此外，随着信噪比的增加，其幅度估计精度和旁瓣电平几乎没有改善。ADMM方法提供的结果略优于1bPER。由于ADMM提供了非常稀疏的谱，因此我们未绘制其旁瓣功率。1bSPICE的旁瓣电平具有竞争力，但其幅度估计存在向下偏差。1bLIKES和1bSLIM在幅度估计性能上相似，且1bSLIM在低信噪比下的旁瓣电平更低。在此示例中，1bIAA在幅度估计精度和旁瓣电平两方面均略逊于1bSLIM和1bLIKES。

上述算法所需的平均计算时间以对数尺度绘制在图4中，横坐标为样本数$N$，网格点数量$M$等于$5N$。1bSLIM使用基于FFT的共轭梯度最小二乘方法。1bLIKES和1bIAA的快速实现则利用了[29]中的戈赫伯格—塞门楚尔分解。需要注意的是，所有四种所提算法均比1bPER和ADMM算法快一个数量级以上。在所提算法中，1bSLIM快于其他三种算法，这归因于1bSLIM每次迭代的计算复杂度较低以及其更快的收敛速度。1bSLIM可在30次迭代内收敛，而其他算法通常需要更多迭代次数。1bSPICE和1bLIKES的计算时间相近，而随着样本数$N$的增加，1bIAA往往比其他算法更慢。

2) PMCW雷达的距离‐多普勒成像

对于PMCW雷达，我们在一个周期内使用长度为$N_1 = 31$且具有$N_2 = 64$个周期的最大长度序列（m序列）CPI作为探测波形。距离和多普勒域中的网格点数量分别设置为$K_r= 4N_1, K_d= 5N_2$。感兴趣区域包含30个目标，其距离‐多普勒位置和功率由图5中彩色标注的‘©’表示。注意，有四个非网格目标用点划线矩形标出。目标的幅度${\alpha_k} {k=1}^{30}$在0.1到1之间随机选取。在实际应用中，时变阈值可由低速率低精度数模转换器生成。为了降低数模转换器的采样率以降低成本，我们采用脉冲重复间隔变化阈值，即阈值在每个脉冲重复间隔内保持恒定，仅在不同脉冲重复间隔之间发生变化。脉冲重复间隔变化阈值的实部和虚部分别从预定义的八元素集合${-h {\max},-h_{\max}+\Delta,…, h_{\max} -\Delta, h_{\max}}$中随机且等概率选取，其中$h_{\max}= \sqrt{\sum_{k=1}^{30} \alpha_k^2 +\sigma^2}/2$和$\Delta= 2h_{\max}/7$。信噪比定义为$10\log_{10} (\sum_{k=1}^{30} \alpha_k^2 / \sigma^2)$，设定为15 dB。

使用一位数据通过1bPER得到的距离‐多普勒成像结果如图5(a)所示。正如预期，1bPER存在高旁瓣问题，导致弱目标被淹没在强目标的旁瓣中。在图5(b)中，我们展示了ADMM方法[15]的结果。ADMM漏检了多个弱目标。1bSPICE的距离‐多普勒图像如图5(c)所示。1bSPICE漏检了一个弱目标，但相比1bPER具有低得多的旁瓣电平，并且比ADMM提供了更准确的目标估计。在图5(d)所示的1bLIKES图像中，每个目标的位置和功率都被准确估计。在图5(e)中，我们展示了1bSLIM的距离‐多普勒图像。1bSLIM漏检了两个弱目标，基本上是因为1bSLIM图像过于稀疏。最后，如图5(f)所示，1bIAA提供了精确的距离‐多普勒成像结果，并识别出了场景中的所有目标。此外，与1bIAA相比，1bLIKES具有明显更多的较强虚假峰（在彩色视图中清晰可见），使得1bIAA成为此示例中的最佳方法。

B. 实验示例

在本节中，我们提供一个实验示例，以展示所提出的用于通过单比特线性调频连续波雷达进行距离‐多普勒成像的单比特加权SPICE算法的性能。实验数据是使用一个24 GHz雷达传感器，带宽为25 MHz，脉冲重复间隔（PRI）为80µs。接收信号由16位模数转换器采样，采样点包含具有未知方差的加性噪声。二维数据矩阵的维度为$N_1 = 64$（距离方向）和$N_2 = 512$（多普勒方向）。距离和多普勒域的网格点数量分别设置为$K_r = 4N_1$和$K_d = 4N_2$。类似于前一个示例中的PMCW情况，我们采用一种脉冲重复间隔变化阈值方案，该方案在每个线性调频脉冲内保持阈值恒定，仅在线性调频脉冲之间改变阈值。假设$A$为高精度数据中的信号功率。同样，在实际系统中，可以粗略估计接收信号的功率来自自动增益控制电路。一位数据是通过将高精度数据与脉冲重复间隔变化阈值进行比较得到的，该阈值的实部和虚部分别从一个八元素集合中随机选取${-