多重比较你用对了吗？

关注“心仪脑”查看更多脑科学知识的分享。

多重比较（multiple comparisons）

是指方差分析后对各样本平均数间是否有显著差异的假设检验的统称。方差分析只能判断各总体平均数间是否有差异，多重比较可用来进一步确定哪两个平均数间有差异，哪两个平均数间没有差异。

为什么不能用t检验而用多重比较了？

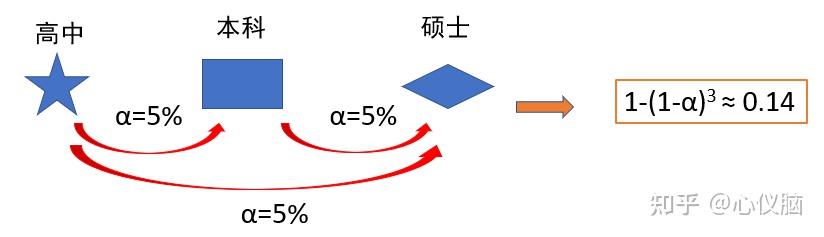
我们来举个栗子，比如研究者想要探究不同的受教育程度的收入情况之间是否有差异。方差分析研究结果已经表明高中、本科、硕士三种受教育程度的收入是有显著性差异的，需要进一步去探究哪两者是有差异，哪两者之间是没有差异的。三种情况两两之间需要进行三次比较，如果采用t检验，每次比较我们犯“弃真”错误的概率是5%，那比较三次，我们累计犯“弃真”错误的概率约等于0.14。也就是说，我们在一次试验中比较的次数越多，犯一类错误的概率就越大，那也就是为什么会选择多重比较。

多重比较方法的选择，真的无迹可寻吗？

SPSS给分析者提供了多种多重比较的方法，根据方差是否齐性分成两部分，其中方差齐性提供了14种方法，方差不齐提供了4种方法。在众多选择中该如何进行选择了？

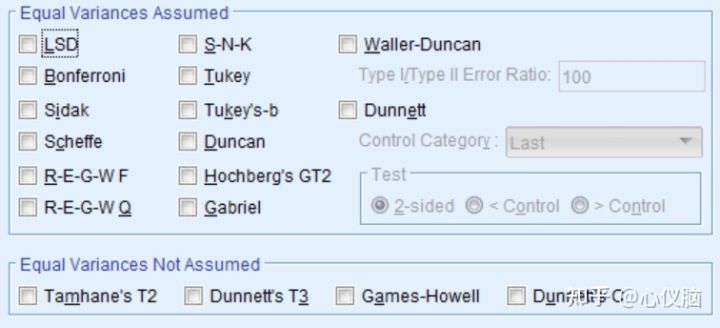
LSD法：

最小显著性差异法(Least Significance Difference)，它实质是t检验，并未对检验水准做出任何校正，所以它对差异最为敏感，但当你比较的次数非常多的时候，比如超过三组之间的比较，我们是不太建议使用LSD方法，因为没有对检验水准α进行校准，所以当比较次数过多时会增大I类错误的概率。为解决该问题，便出现了Sidak法和Bonferroni法。

Sidak法和Bonferroni法：

都为LSD的修正，其灵敏度为LSD法>Sidak法>Bonferroni法。所以Bonferroni法建议在比较组别数量较少时使用，当比较的次数较多，比如10次以上，不太建议使用该方法，会出现较多的假阴性结果。

Tukey法：

其思想和LSD法类似，但比LSD方法保守，即灵敏度不如LSD。Tukey法要求比较的样本容量相差不大，一般用于样本容量相同的组之间均数的比较。

Scheffe法：

当各组人数不相等，或者想进行复杂比较时，用此法比较稳妥。它检验的是各个均数的线性组合，而不是只检验某一对均数间的差异，方法相对比较保守，检验效能高，适用多种情况。

总结来看：

1. 方差齐，比较的组别较少——Bonferroni
2. 方差齐，各组样本量相同——Turkey
3. 方差齐，各组样本量不同——Scheffe
4. 方差齐，多个实验组与对照组做比较——Dunnett

全文完结，整理不易，看不完记得收藏，最后希望点赞支持一下！

了解更多，请关注“心仪脑”公众号！