吉林大学统计计算期末复习（第二章第二部分）

第二部分，我们主要关注非均匀随机数的生成。

同时我们也分为，离散型与连续型进行讨论。

2.3.1         前置知识讨论

前置知识，主要在于定理6.1，6.2 的证明过程

证明：

证明：

逆变换法的原理在这张图中展示的比较直观：

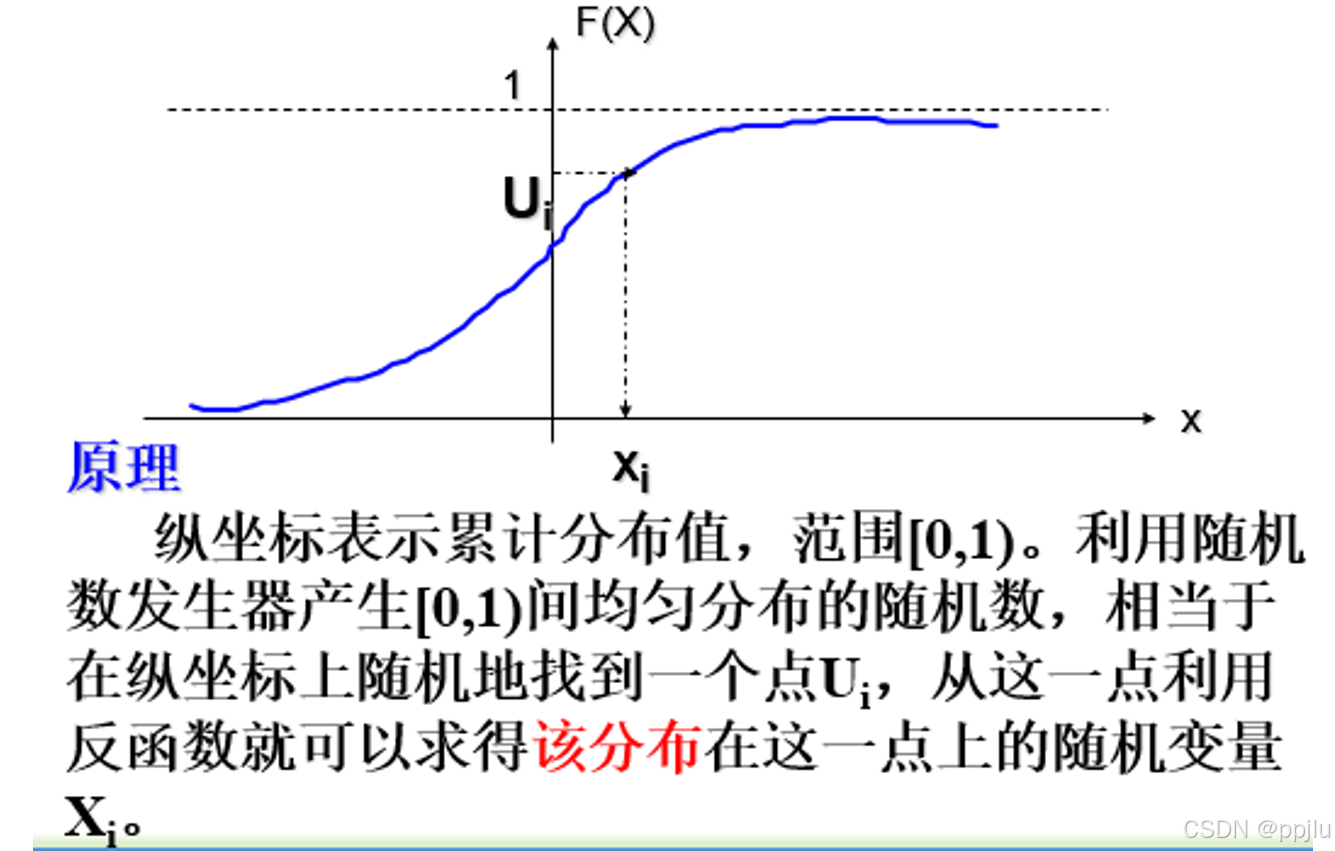
2.3.2        逆变换法生成离散型随机数

这一部分其实相对来说好理解些，更多的需要背诵记忆

1.        离散均匀随机数生成

2.        几何分布随机数生成

（首先，要知道几何分布是啥）

（注意所有的逆变换，都需要关注原函数是个什么东西）

:代表不小于x的最小整数

3.        二项分布随机数生成

其实就是咱们高中学的：超几何分布

标准流程方法如下：

4.        泊松随机数生成

泊松分布：

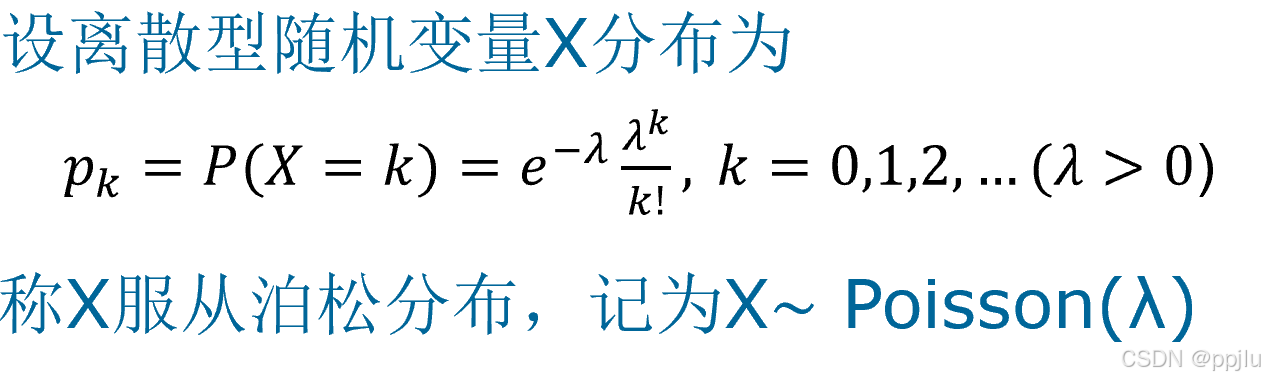
生成法：

2.3.3        逆变换法生成连续型随机数

最简单与基本形式

1.        两种三角分布

（了解即可，主要和后面的复合法有点关系）

（1）右三角分布

（2）左三角分布

2.        指数分布随机数

3.        利用指数分布生成泊松随机数

原理：N（t）代表截至时间 t 时，发生的事件数。

例如N（5）=30，代表时刻5时，事件发生了30次

那么我们在这时，假设事件发生一次，需要时间（指数分布的来源）

那么我们求，N（1）的最大值，就是1时间内，最多发生了多少件事（生成的是泊松随机数）

老师解释如下

求解算法如图：

2.3.4        利用变换生成随机数

（主要重点在于，所能获得但不能直接生成的量，和不易获得但能直接生成的量之间有关系）

概率论中的式子很重要：

二阶的这么玩

下面的应用：

推导过程如下：
 

2.3.4        舍选法I

过程不难，理解这个就行

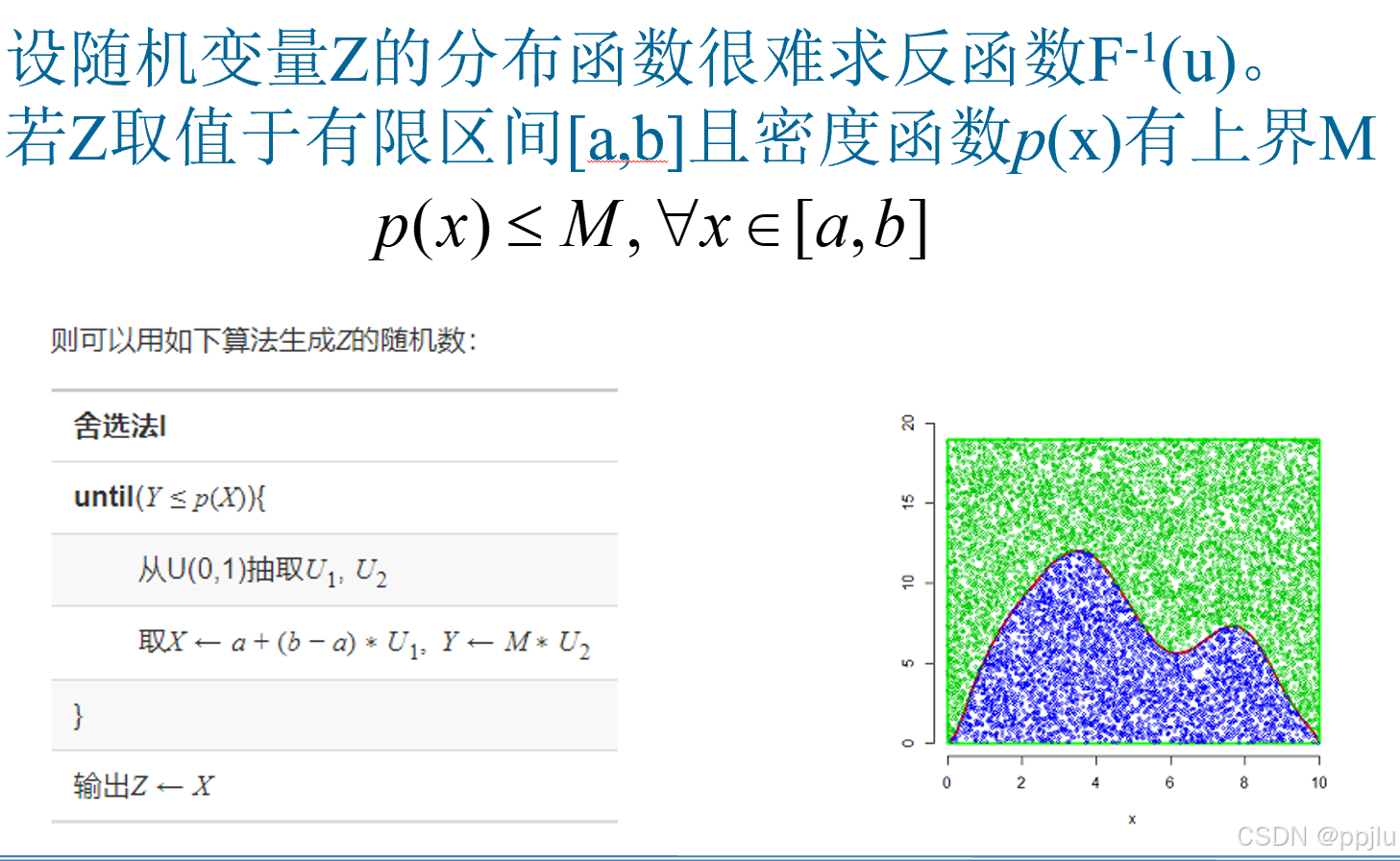
优缺点

1.        舍选法生成box-Muller随机数

2.3.5        复合法

我的理解是更多的化成两步，进行随机数的获得提取（感觉在这一块老师说的不是太多）

一个应用就是梯形分布的一个应用

直接用逆变换法求随机数太麻烦，所以决定看看有什么巧妙地方法

劈成了两部分，我理解用的时候，先去取个0-1的随机数，

在某个范围内，抽用作三角分布。在另一个范围里，用矩形分布生成即可

2.3.6        随机变量的生成

建议看两页ppt算了，不知道会怎么出