吉林大学统计计算期末复习（第二章第一部分）

废话不多说，根据SYF老师知识点展开

架构：

随机数分为：（1）均匀随机数 （2）非均匀随机数

非均匀随机数又分为：（1）离散型 （2）连续型

在第一部分均匀随机数，我们主要关注，整数均匀随机数的生成

2.2        均匀随机数的生成

前置知识，理解什么叫同余，与同余的一些性质（其实离散数学里很多提到）

（性质4在后面证明阶数的过程中很重要）

2.2.1        线性同余发生器（LCG）

公式如下图所示

PS：这里需要注意，我们真正生成的随机数是Rn，生成后的Xn需要除以m，才是我们的目标

线性同余发生器又分为两类：

2.2.2        混合同余发生器

首先记住，当我们是混合同余发生器时，公式如下：

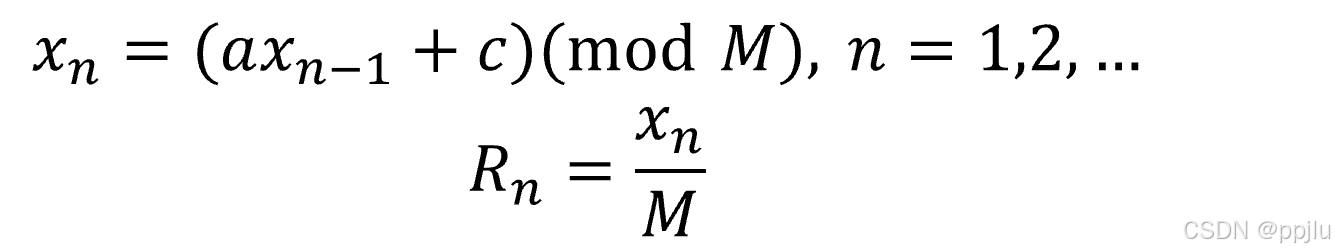
（一定要记得，我们的目的是为了获得Rn）

此时的C>0,所以代表，Xn是可以取0的哦（很重要）

所以，Xn的取值范围为(记住我们一直是取余运算哦)

所以如下性质便成立（等差数列的知识就不介绍了）

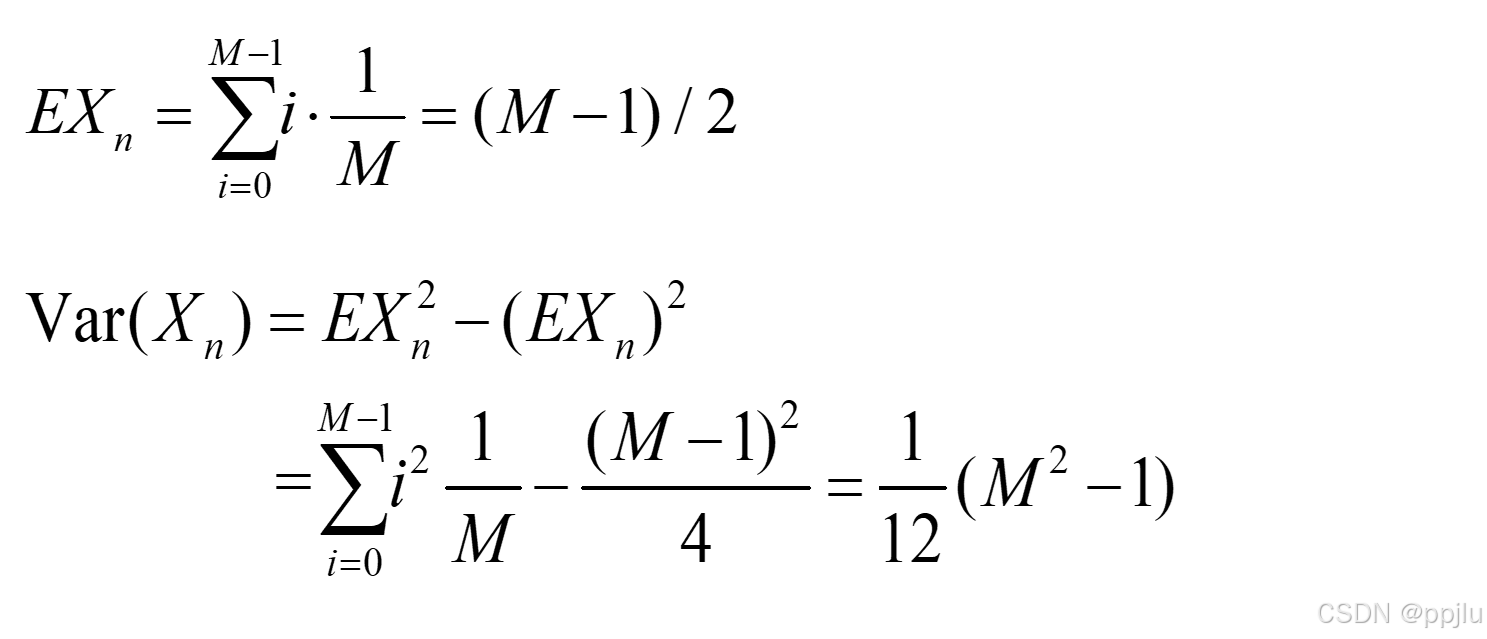
注意平方和公式：

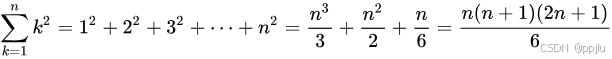
所以除以M，后

2.2.3        乘同余发生器

性质介绍：

在这里，X的取值，是从1开始的哦。

因为c=0，如果x=0，发生器就只能生成0了，产生不出来别的数了（废了）

以下为老师讲述的证明，大概回忆版

第一次作业推导：

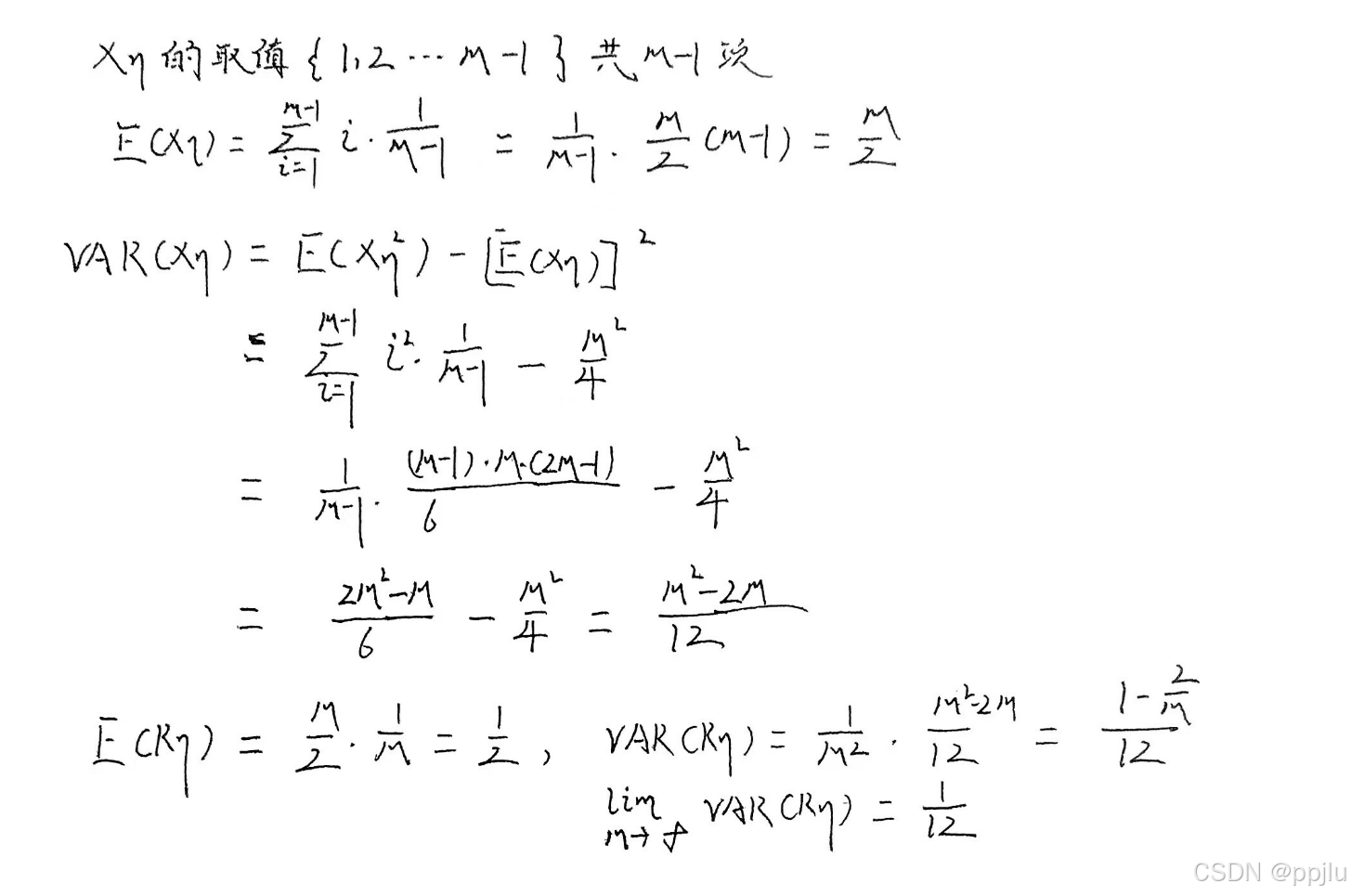
2.2.4        随机数检验的意义

我确实没有找到老师的原话，可能还是学在吉大看的不够认真

（如果有谁看着了please告诉我一声）

查阅一些的资料，可以参考一下

（1）检验产生的随机数是否能代表总体样本

（2）检验随机数样本是否具有独立性

（3）检验随机数样本是否具有组合规律性

（4）参数检验

2.2.5        KS检验

直接看老师给的文档即可，感觉也不是很困难（建议直接看表）

作用可能是：检验多样本之间的分布是否相同