目前我们到达第三章啦(可以给自己鼓鼓掌.jpg)
第三章我们主要分为两个部分
第一部分,我们致力于使用随机模拟的方式,解决积分问题(即排队论前的所有知识)
第二部分,我们主要介绍了几种模型(排队论,MCMC),以例题为导向
这篇博客,我们介绍第一部分
3.1 随机模拟介绍
3.1.1 数学建模的特点
(其实增加理论假设,排队论中也有)

缺点(单纯理论分析,存在的普遍问题,说白了还是不放心)

3.1.2 随机模拟方法的特点

(注意这个对维数增加不明显,代表“可以解决维数诅咒问题”)
3.2 随机模拟积分
开始介绍方法之前,大家一定要记住
这个部分的主线是,求解这个问题
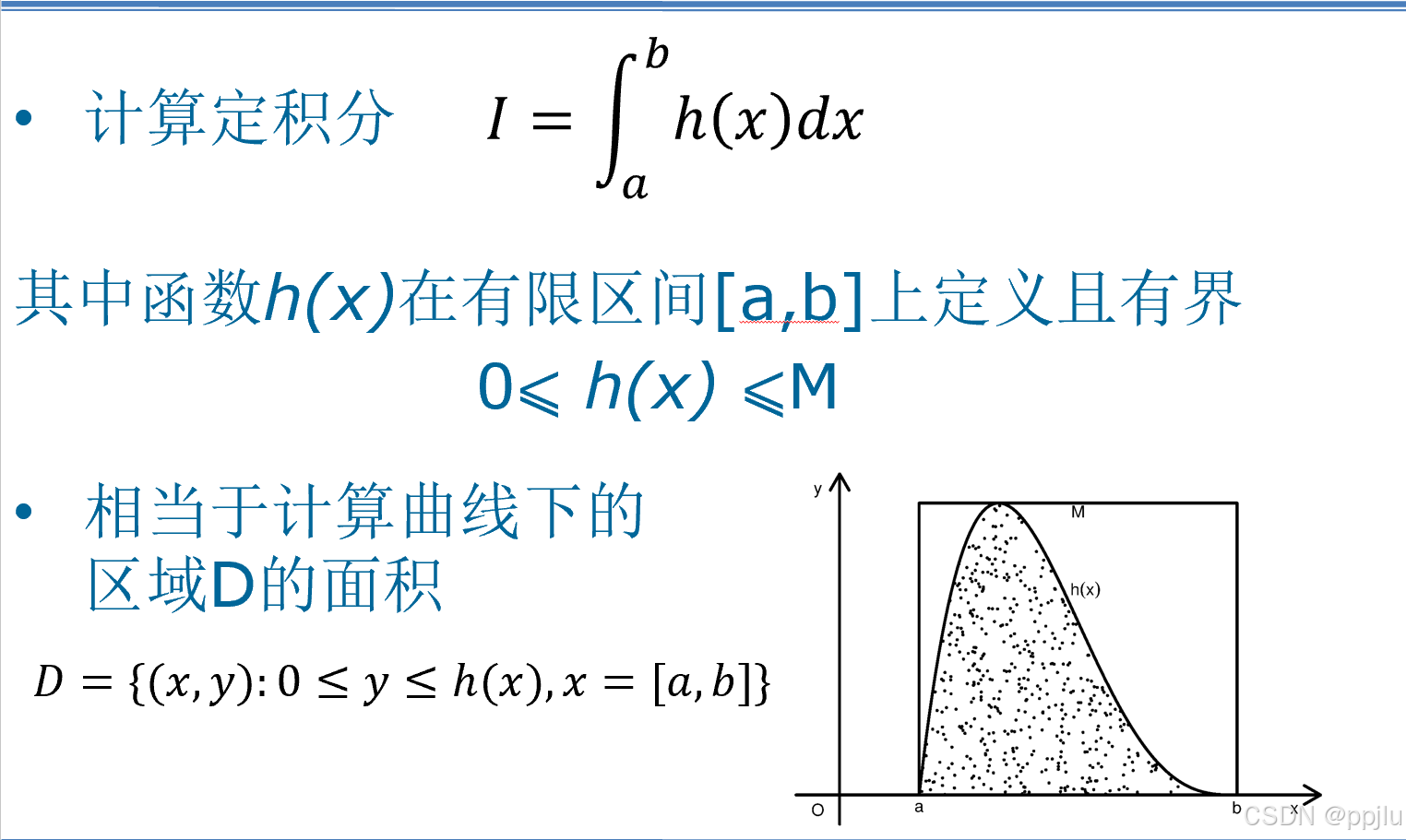
我们学习的所有方法,都是为了解决这个积分问题
3.2.1 随机投点法
首先,我们的投点法中,投出去的点,是满足伯努利分布的
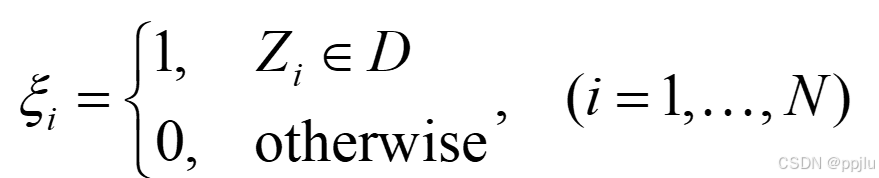
(这个跟后来的算方差的公式有关)
原理的本质很简单:
往区域里投点,投到范围里的点算1,范围外的点为0。
投N个点,看N个点里,有多少个1,从而推算出它的比例
然后用整个矩形的面积进行相乘,得到我们的积分值。
![]()
V(D)就是I 的面积, V(G)是矩形面积
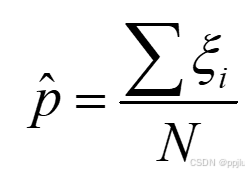
↑
投点法的应用
得到的应用(老师那个是进一步的推论)
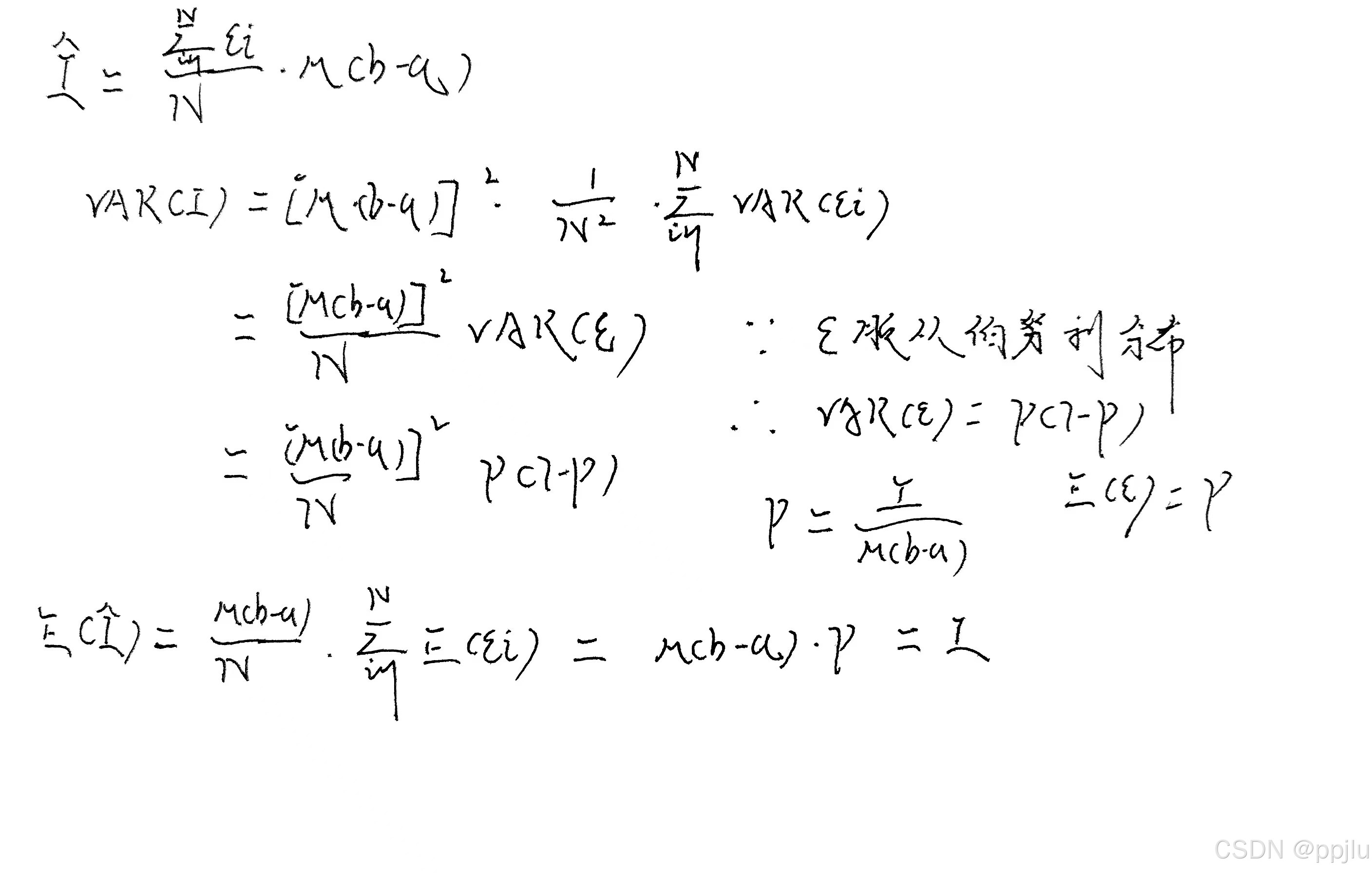
3.2.2 平均值法
为啥叫平均值法呢
因为在这里咱们假设,X在【a,b】上均匀分布
并且,咱们再后面的预期估计过程中,用的是平均值来估计预期
(仔细观察这个E的来源,就是均值的方法)
3.2.4 高维定积分
如果上面看明白的话,其实就是把(b - a)换成 即可,剩下都一样
即可,剩下都一样
1. 随机投点法
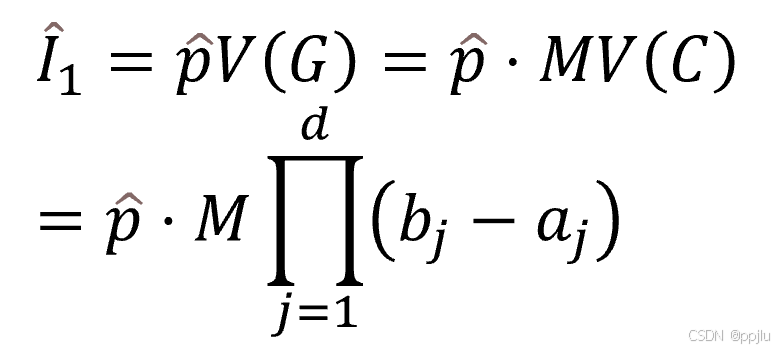
V(C)就是区别
V(C)就是这个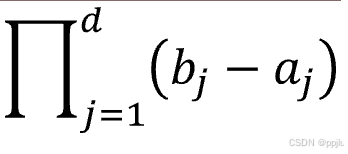
2. 平均值法
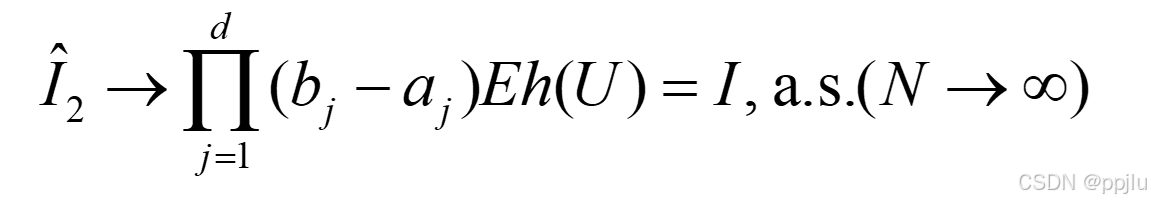
发现式子的区别了嘛(仔细看一看)
他们之间除了抽样出来的数不一样,然后就是M的有无
3. 两种之间的方差比较
前提:假设M=1(最关键的一点)
所以两个式子就成:
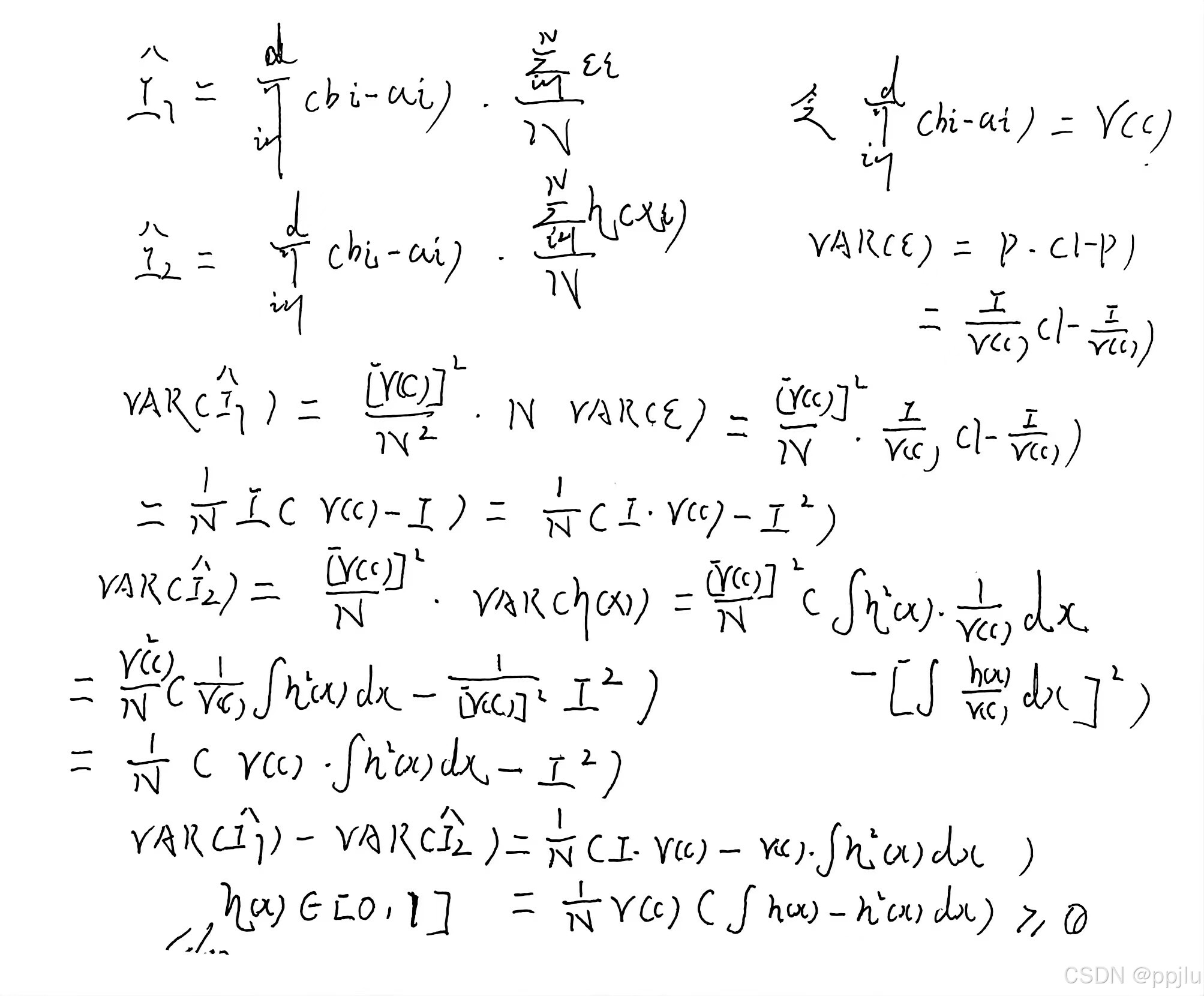
(建议多手推着玩,比较锻炼,并加深式子的记忆)
3.3 重要抽样法
可以简单理解成,现在密度函数,不是常数了(在平均值法里,假设成了均匀分布嘛)
现在的密度函数是 g(x),所以咱们套入原来的式子,就成这样了
但明显,咱们想要的是
所以呢,咱们就要对 做一些改动
咱们抽
就获得了咱们想要的
而标准重要抽样呢,又牵扯到咱们想算期望的问题上了
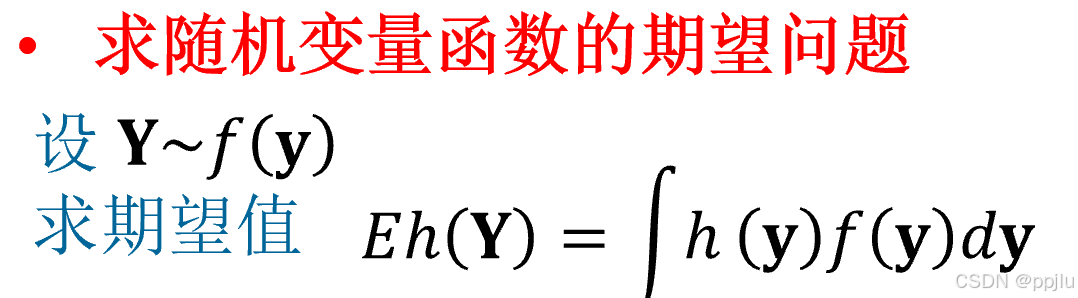
咱们怎么办呢
也是已知,X的密度函数是 g(x)
咱们用抽到的X来估计整个Y的式子
那式子就得变成这样:
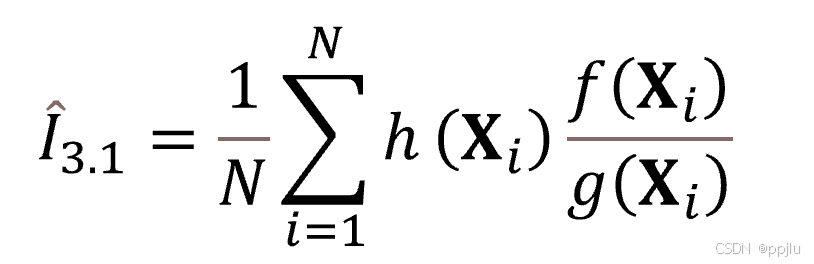
这样求Y的期望,就转化成利用X进行操作的过程了
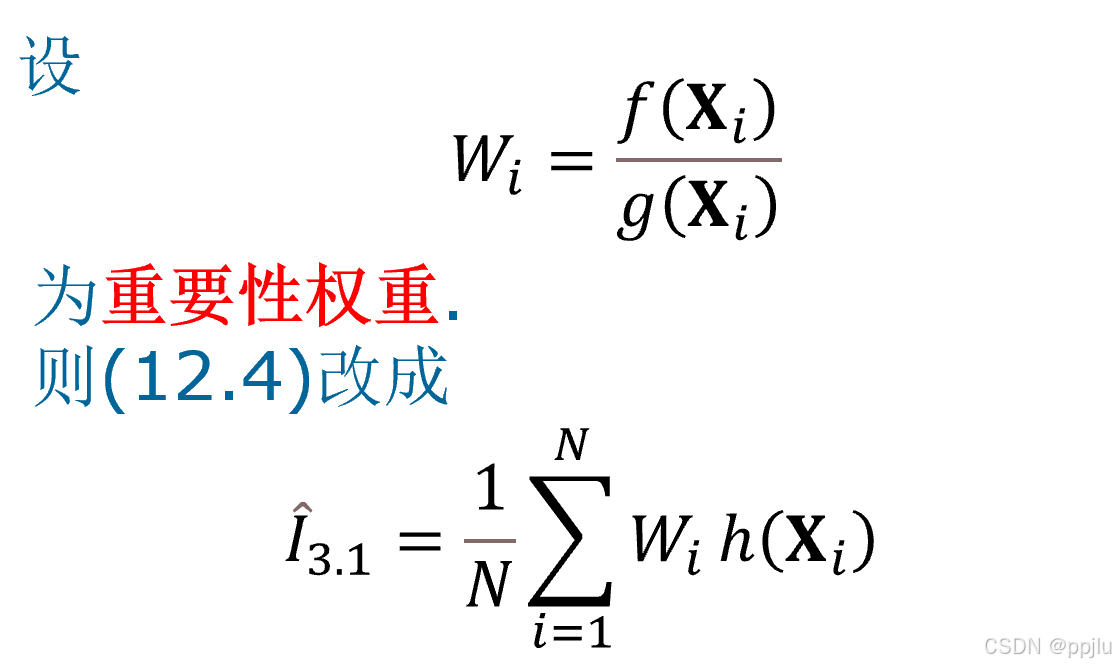
引入了wi这个量

这就是标准化的式子
(注意里面由于Y的分布密度函数难以知道,只能通过上下同时相除,除去其中的c,从而得到结果)
3.4 分层抽样法
通过人为分段,目的减小方差
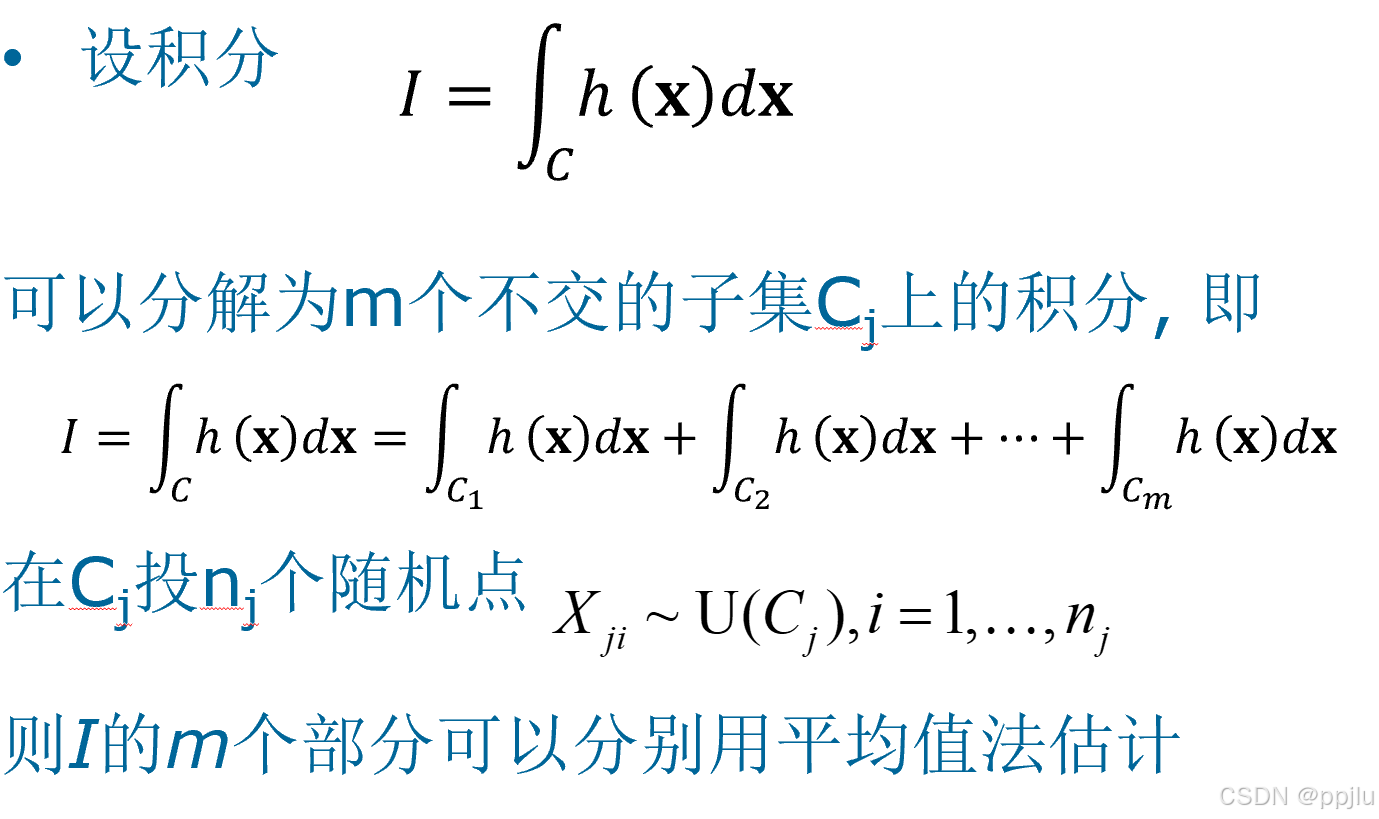
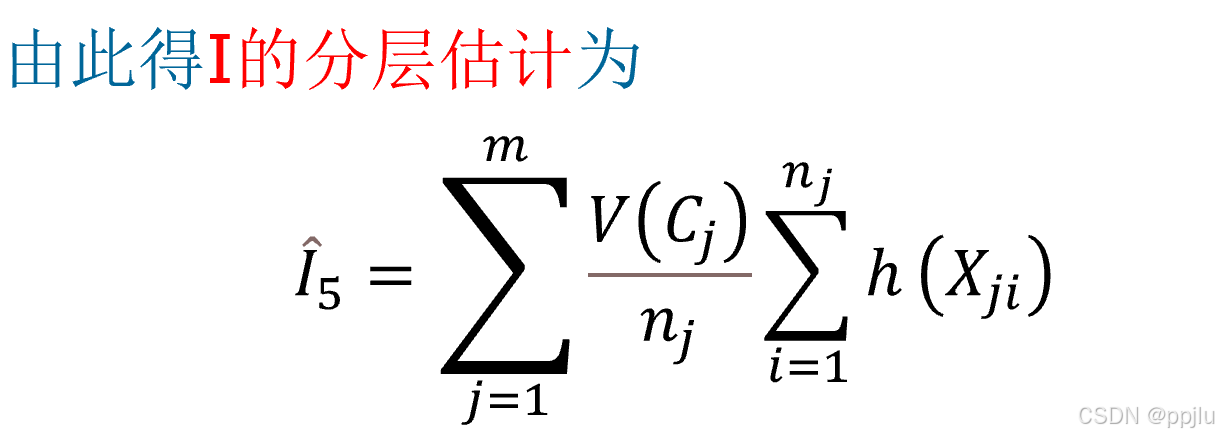
(很明显,本质上用的还是平均值法)
下面例题很好的利用了双期望定理,人为创造一个条件

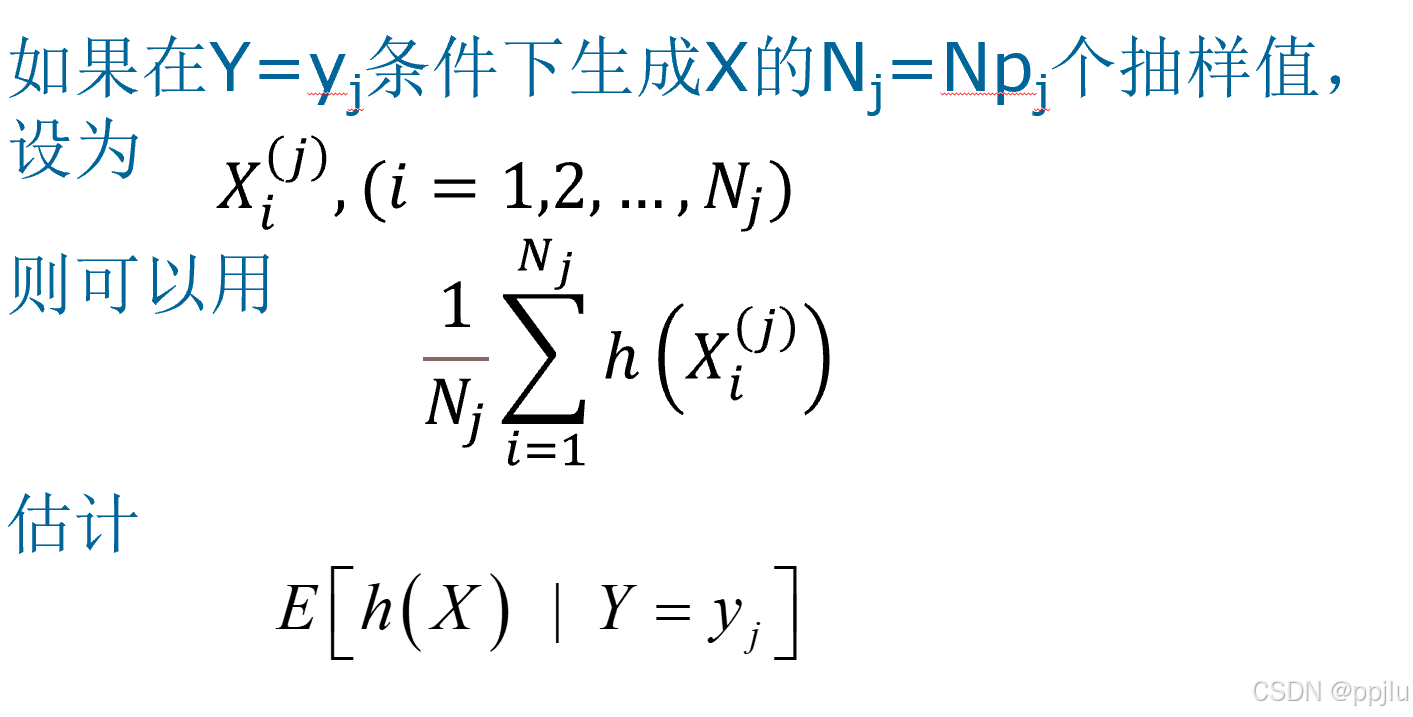

以下是很好的一个例题,建议学习
(人为创造分段,进而进行式子的变化)






















 1316
1316

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








