理解定义域，值域，和陪域(到达域)

定义域 和 值域

定义域 和 值域很容易理解

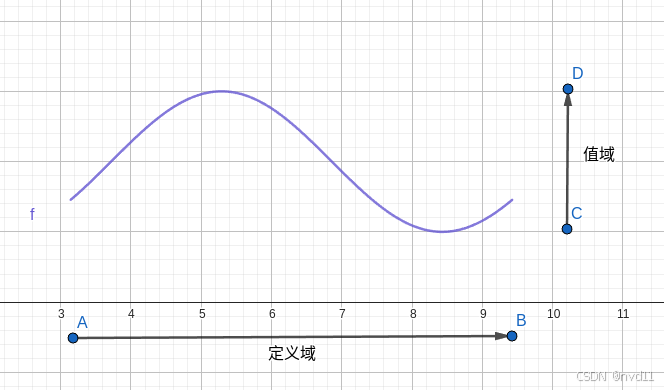
简单地讲：
定义就是所有函数输入值的集合
值域就是基于定义域， 所有函数输出值的集合

例如：
对于 函数
$f(x)=2^x,x\in [-2,2]$

定义域 就是 [-2, 2], 值域就是[0.25 , 4] 很明显

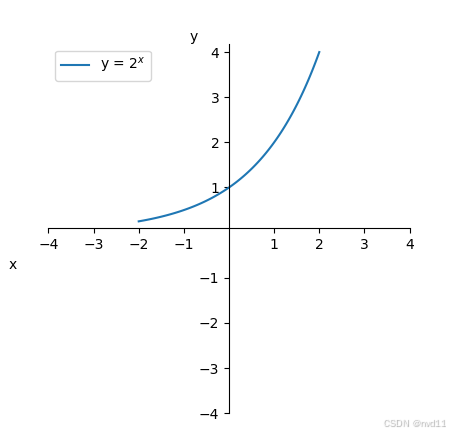
定义域(Domain) 是函数定义的关键部分

定义域往往是 human 定义函数的一部分， 也就是讲定义域是人类来定义的.

下面两个函数， 虽然数学式一样， 但是由于定义域不同， 他们实际上就是两个不同的函数

$f(x)=1+x,x\in [-\infty ,0]$
$f(x)=1+x,x\in [0,1]$

值域(Range) 是精确的，实际的函数输出的值集合

例如上面的例子
对于 函数
$f(x)=2^x,x\in [-2,2]$

其值域不是人类定义的， 是由函数本身的规则(包括定义域) 推导出来的
值域就是[0.25, 4] 而不是 其他的集合。

现实世界上并不是所以值域都能准确推算， 大约的值域

假如一棵树每年都会长高大约20厘米

那么我们可以定义1个函数关于年龄和树的高度， 而且我们可以定义年龄的范围(定义域)
$f(x),x\ge 0\wedge x<=100$

但是值域很难精确决定， 首先一棵树的生长因数太多了， 它不是每年生长固定的长度， 到一定年龄甚至停止生长。
所以这个函数的值域是很难确定的

但是我们可以基于其他因数考虑， 一棵树的高度不会超过200米， 所以我们可以定义1个大约的值域[0, 200], 这个大约的值域就是所谓的陪域。

函数的集合定义

所以上面这个大于的值域， 我们可以理解为函数的允许输出值。也就是将， 函数的正式定义中， 我们需要描述这个函数的允许输入(定义域) 和 允许输出(陪域)

对于这种定义， 我们最好是使用集合(Collection)

正式定义：

函数把1个集合的每1个元素联系到另1个集合(可能是同1个)里1个单独的值

这个定义里， 函数包括两个集合， 输入集合 和 输出集合

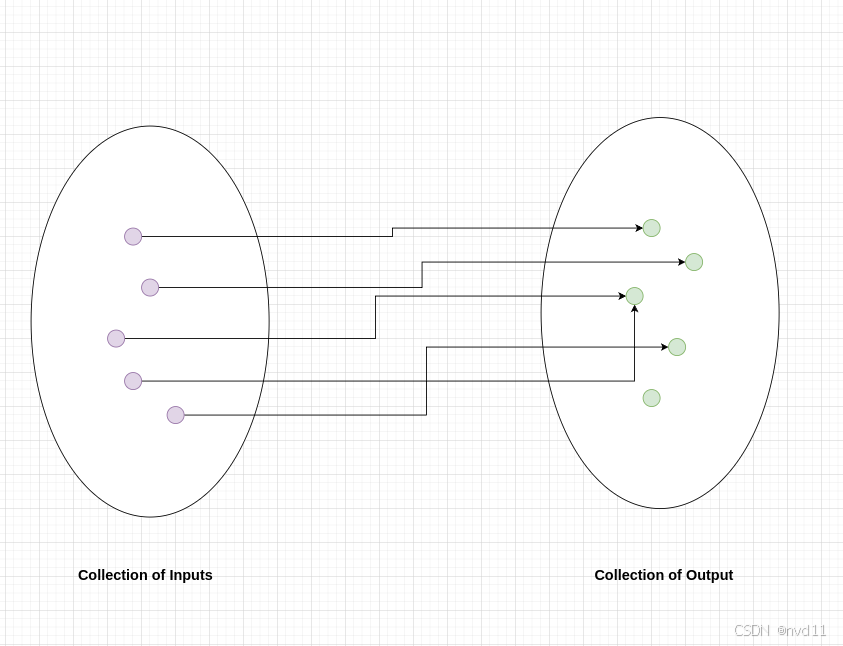
注意上图， 多个不同的输入值可以指向相同的1个输出值

而下面这个集合关系并不是函数， 因为函数不允许同1个输入值有多个不同的输出值

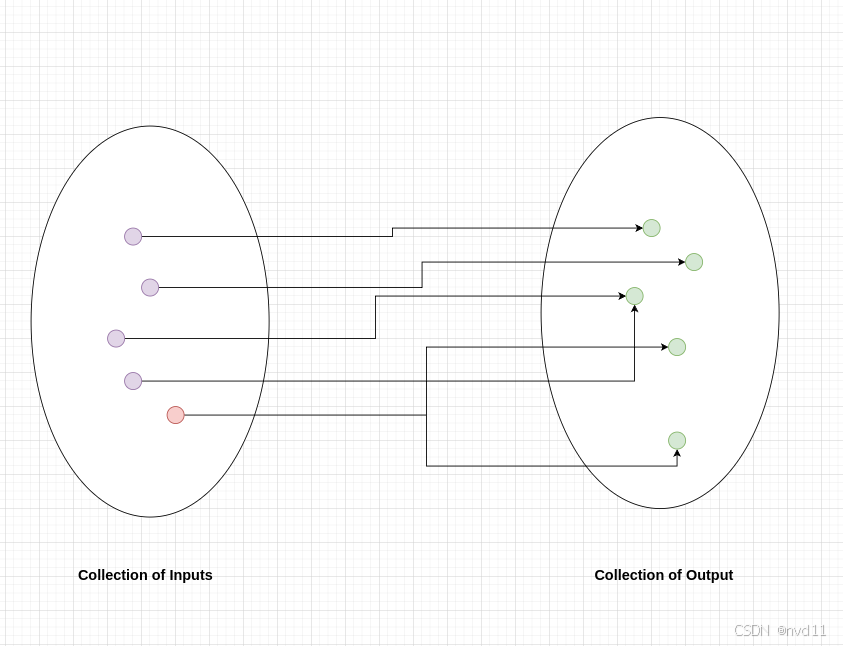
函数的集合定义里的定义域， 值域和陪域

在集合定义里。

定义域

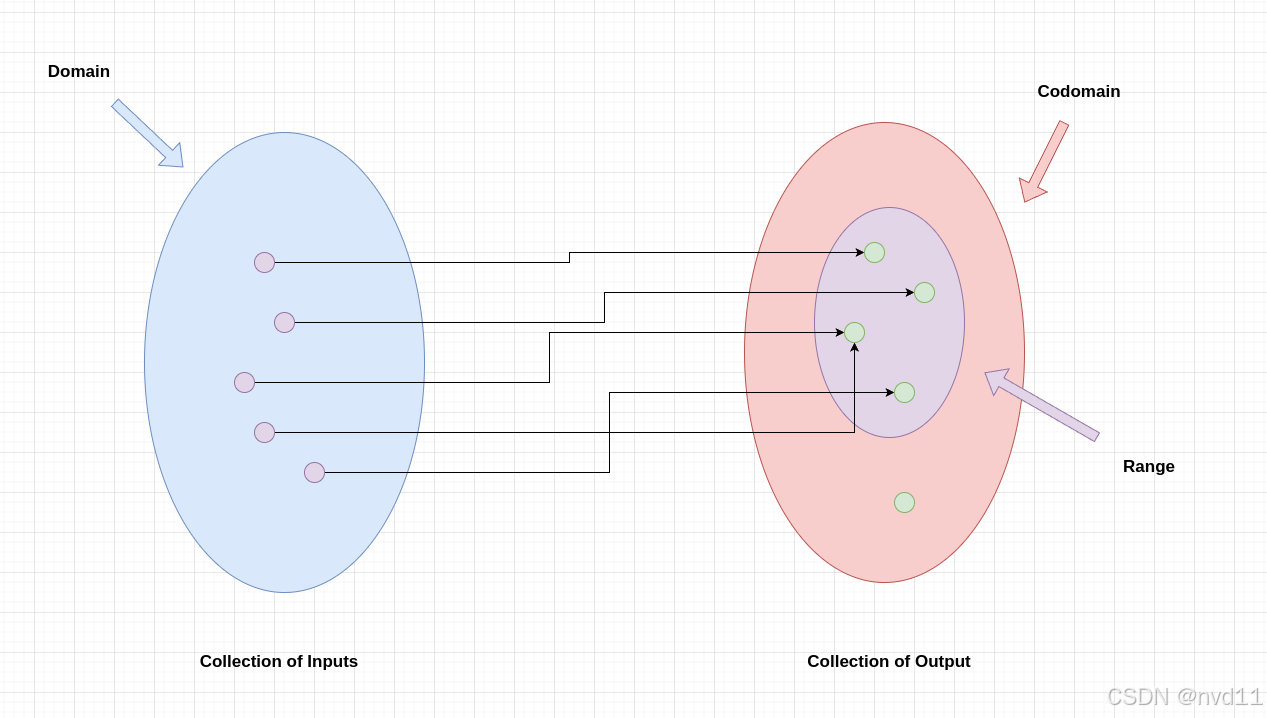
允许输入到1个函数的集合就是定义域， 就是下图的 Collection of Input , 其实这个集合就是定义域

陪域

函数的可能输出就是陪域
下图的 Collection of Output

值域

而函数的实际输出集合叫值域

可知值域是陪域的1个子集合， 如下图

1个具体函数例子

对于函数
$f(x)=x^2,x\in N$

定义域是自然数 N
值域是 $1^2,2^2,3^2...$ 也就是完全平放数列的所有元素集合 ， 也可写成{n2 ∣ n∈N}\{n^2 \ | \ n \in N\}{n2 ∣ n∈N}
陪域可以是$[0,\infty ]$, 也可以是N, 或者R， 取决于你怎么定义

具体一点

对于 $N\to R,f(x)=x^2$

这时， N是定义域， R是陪域， 值域$1^2,2^2,3^2...$

对于 $N\to N,f(x)=x^2$
N是定义域， 陪域也是N， 值域还是$1^2,2^2,3^2...$

陪域的记法

数学家喜欢以简单的符号来代替冗赘的文字，描述定义域和陪域也一样。
上面都使用过了
$f:R\to R$
意思是定义1个 从 实数集合 到 实数集合的函数f, 其中前面的R是定义域， 后面的R是陪域， 至于值域先在还不知道呢

为什么需要陪域

1. 有时函数的定义需要引入陪域

例如1个参数的平方根是函数吗：
$f(x)=\pm \sqrt{x}$

明显不是， 因为 9 的平方根有两个, -3 和 3

但是如果我们加上陪域
$f:R->[n|n\in R\wedge n\ge 0],f(x)=\sqrt{2}$
这个就是1个函数了， 因为我们在定义里限制了函数的陪域是正实数

2. 陪域是满射定义的其中1个关键项， 至于什么是满射， 参考我下一篇博文