函数和图像

函数和图像

• 函数的定义域、上域、值域和垂线检验
• 反函数和水平线检验
• 函数的复合
• 奇函数与偶函数
• 线性函数和多项式的图像
• 有理函数、指数函数、对数函数图像的回顾
• 处理绝对值

函数

函数的定义

函数是将一个对象转化为另一个对象的规则。被转化的对象称为输入，来自称为定义域的集合。转化后的对象称为输出，来自称为上域的集合

我们通常这样定义一个函数$f(x)=x^2$

请注意这不代表f(x)是一个函数，准确的说f(x)是把这个变换规则应用于变量x后得到的果。而f是一个变换规则，即f才是我们通俗意义上所说的函数

一个函数必须给每一个有效的输入指定唯一的输出

定义域：使函数有意义的值的集合

值域是所有可能的输出组成的集合

值域和上域的区别

值域实际上是上域的一个子集。上域是可能输出的集合，值域是实际输出的集合

区间表示法

$[a,b]$是指从a到b端点间的所有实数，包括a和b。所以$[a,b]$指的是所有使得$a<=x<=b$成立的x的集合，像这种形式表示的区间，我们称为闭区间

$(a,b)$指的是介于a和b之间但不包括a和b的所有实数的集合。这种形式的区间被称为开区间

两者可以混合使用，如$[a,b)$表示的是介于a和b之间、包括a但不包括b的所有实数的集合。这样的区间被称为半开区间

求定义域

定义域会出问题的三种情况

1. 分数的分母不可能是0
2. 不能取一个负数的平方根（或四次根、六次根等）
3. 不能取一个负数或零的对数

实际做题中求定义域时，牢记这三种情况即可，必须同时满足

函数图像以及垂线检验

什么是函数的图像

所有坐标为(x, f(x))的点的集合，其中x在其定义域中

还有一种思路。从某个实数x开始，如果x在定义域中，就画出(x,f(x))的点，这个点在x轴上的点x的正上方，高度为f(x)。如果x没有在定义域中，不能画任何点。对于每个实数x，重复这个过程，即可构造出函数的图像

垂线检验：如果你有某个图像并想知道它是否是函数的图像，就去看是否任何相对于x轴的垂线和图像相交多于一次。如果是，它就不是函数的图像。

反函数

对于在函数f值域中的任意y，都只有唯一的x值满足f(x)=y。函数f的反函数f^-1定义如下

1. f^-1的定义域和f的值域相同
2. f^-1的值域和f的定义域相同
3. f^-1(y)的值就是满足f(x)=y的x。所以

​ 如果f(x)=y, 那么f^-1(y)=x

水平线校验

如果每一条水平线和一个函数的图像相交至多一次，那么这个函数就有一个反函数

求反函数

两种方式

第一种方式写出y=f(x)，然后解出x即可

第二种方式画出原函数的图像，在图像上画一条y=x的直线，然后将这条直线想象为一个双面的镜子，反函数就是原始函数的镜面反射

限制定义域

如果水平线校验失败，我们还想求反函数的话，可以通过限制定义域来进行

反函数的反函数

如果f有反函数，那么对于在f定义域中的所有x，f^-1(f(x))=x成立。同样地，对于在f值域当中的所有y，都有f(f^-1(y))=y成立

换句话说，反函数的反函数就是原始函数

总结如下

如果一个函数f的定义域可以被限制，使得f有反函数f^-1，那么

• 对于f值域中的所有y，都有$f(f^{-1}(y))=y$
• $f^{-1}(f(x))$可能不等于x；事实上，$f-1(f(x))=x$仅当x在限制的定义域中才成立

函数的复合

假设有一个函数$f(x)=h(g(x))$，这是一个复合函数，可以写成$f=h\circ g$​，即f是g与h的复合，注意运算顺序和阅读顺序相反

奇函数和偶函数

如果对f定义域里的所有x都有$f(-x)=f(x)$,则f是偶函数

当对f定义域内所有x都有$f(-x)=-f(x)$时，f是奇函数

大多数函数是非奇非偶的。只有一个函数是既奇又偶的，它就是$f(x)=0$(零函数)

如果一个函数是奇函数，并且0在其定义域内，则$f(0)=0$

偶函数的图像关于y轴具有镜面对称性

奇函数的图像关于原点有$180^{\circ }$的点对称性

证明一个函数是奇函数还是偶函数的方法

将每个x替换为(-x)，并计算f(-x)，然后化简结果。如果得出原始表达式f(x)，f就是偶函数；如果得到原始表达式的负值-f(x)，f就是奇函数；如果得到的结果一团糟，则非奇非偶（也有可能是化简不充分）

线性函数的图像

形如$f(x)=mx+b$​的函数叫作线性函数

如果m>0，函数递增

如果m<0，函数递减

m的绝对值越大，图像就越陡

如果m为0，图像是水平的

直线通过(0,b)点

画线性函数的图像时，只需要确认两个点即可。通常这两个点分别为y轴的截距和x轴的截距，但这个方法，在两种情况下不适用

• b=0
• m=0

直线方程的点斜式

如果已知直线通过点$(x_0,y_0)$，斜率为m，则它的方程为$y-y_0=m(x-x_0)$​

知道两点，如何求斜率？

如果一条直线通过点$(x_1,y_1)和(x_2,y_2)$，则它的斜率等于$\frac{y_2-y_1}{x_2-x_1}$

常见函数及其图像

多项式

以1、$x$、$x^2$、$x^3$等为基本项

基本项$x^n$的倍数叫作$x^n$的系数

最大的幂指数n叫作多项式的次数

从$x^0$到$x^7$的图像，奇次幂之间很相似，偶次幂也很相似

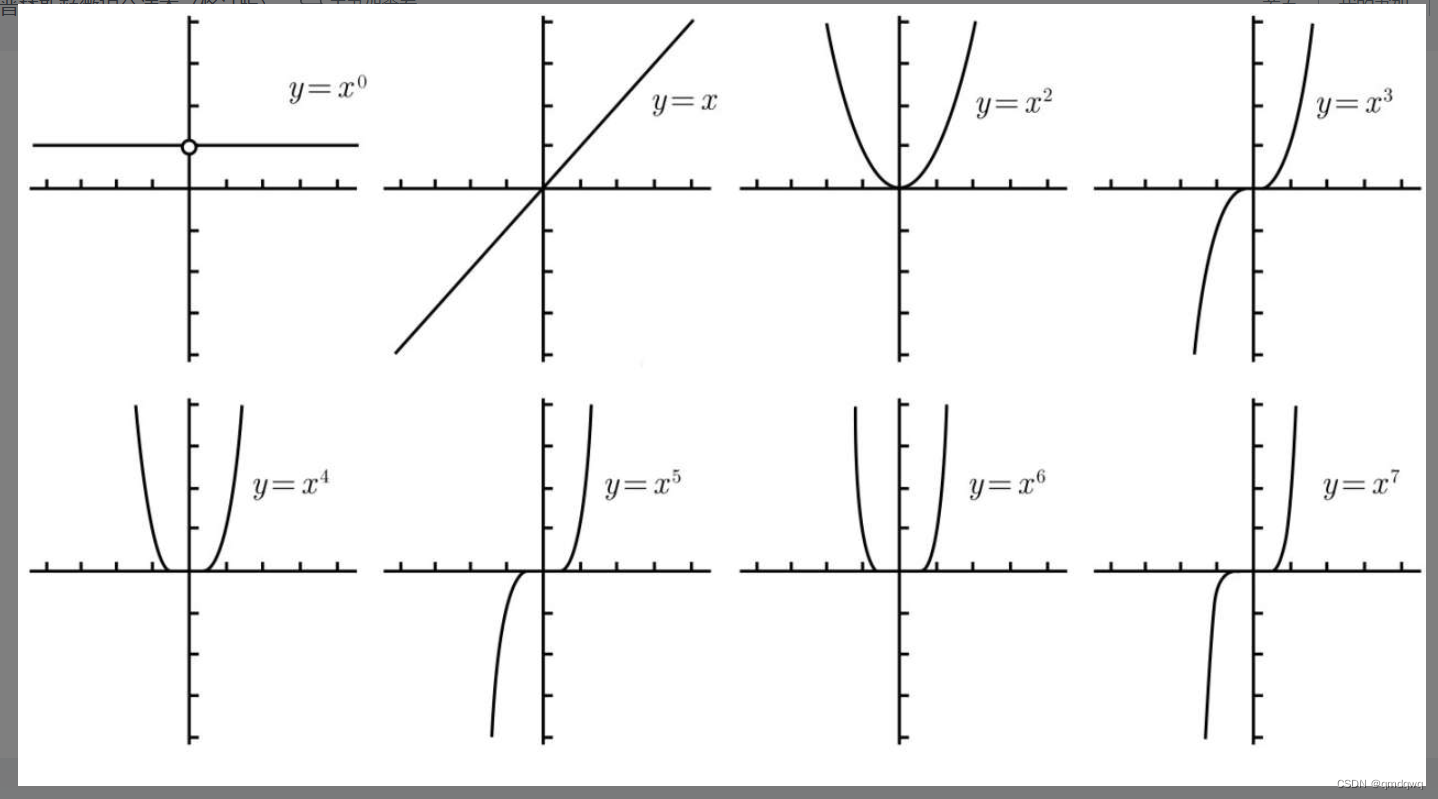
多项式图像两端的走势由最高次数的项的系数决定，该系数叫作首项系数，只需考虑首相系数正负以及多项式次数的奇偶就能判断图像两端的走势

有理函数

下面是一些有理函数的图像

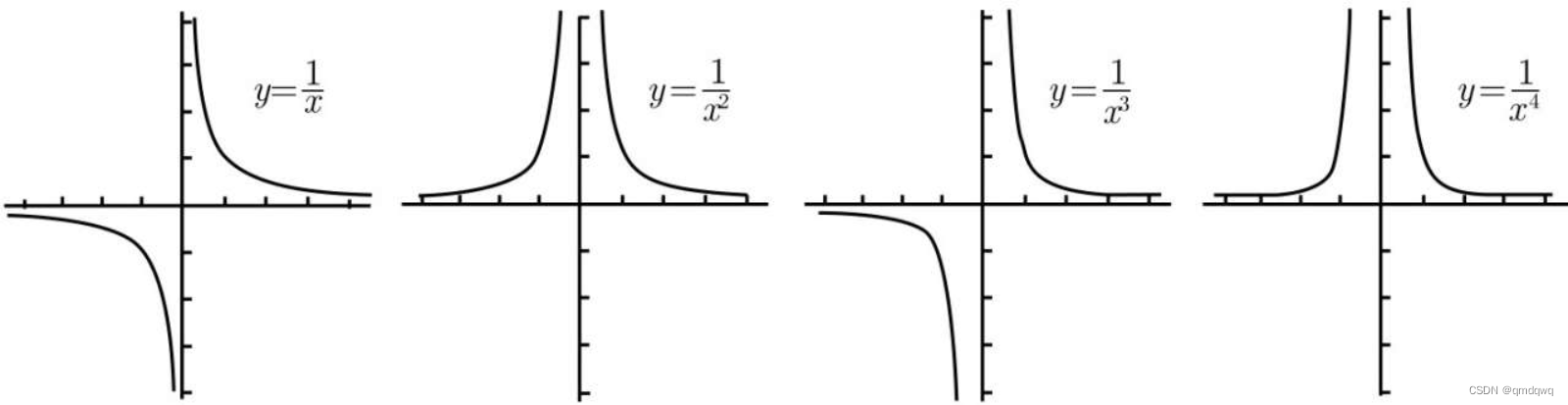
奇次幂之间很相似，偶次幂也很相似

指数函数和对数函数

下面是$y=2^x$的图像，$y=b^x(b>1)$的图像都与这图类似

• 该函数的定义域为全体实数
• y轴的截距为1并且值域为大于零的实数
• 左端的水平渐近线为x轴，该图像无限接近于x轴，但永远不会接触到x轴
• 对于任意$b^x(b>1)$，都有$b^{-x}=(\frac{1}{b}{)}^x$​
• 该函数有反函数，它的反函数就是$y={\log }_{b}x$
  • 该函数的定义域为$(0,+\infty )$
  • 值域为全体实数
  • y轴为垂直渐近线

带有绝对值的函数

形如$f(x)=\left|x\right|$的函数，被称为绝对值函数，该函数的定义为
$$\left|x\right|=\{\begin{array}{ll}x,& \text{如果 }x⩾\text{ 0}\\ -x,& \text{如果 }x<\text{ 0}\end{array}$$

它表示数轴上0和x的距离，更一般而言

$\left|x-y\right|$是数轴上x和y两点间的距离

如果已经知道一个函数的图像，以x轴为镜子，把x轴下方的图像映射上来，x轴上方的图像保持不变，即可得到这个函数绝对值的图像