硬件基础知识补全【一】电阻

原创已于 2025-11-03 09:37:19 修改 · 1k 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#单片机 #嵌入式硬件 #1024程序员节

于 2024-10-24 22:32:22 首次发布

硬件设计专栏收录该内容

10 篇文章

订阅专栏

一、电阻理论

1.1 电流定义

电流：电流的强弱用电流强度来描述，电流强度是单位时间内通过导体某一横截面的电荷量，简称电流，用 $I$ 表示。1 秒内有 $6.2415093\times 10^{18}$ 个元电荷通过横截面的电流，定义为 1 安 ( $A$ )。

电压：电压就是电势能，电压，电势能是指电子在电路中的动能。单位通常为伏特 ( $V$ )。电压是电力系统中的一种重要概念，它决定着电流流动的强度电压越高，电子移动的越快，电流就会越大，而电压越低，电流就会越小。

电阻：电荷在导体内运动时，形成电流。导体中的分子，原子等其他粒子阻碍电荷移动，进而阻碍电流，这种阻碍作用，我们称之为电阻。

1.2 欧姆定律与电阻定义式

电阻单位为欧姆 $\Omega$ ，电阻越大，阻碍作用越大，通过导体的电流自然就越小。

$I=\frac{U}{R}$

$I$ = 电流
$U$ = 电压
$R$ = 电阻

但是真正决定电阻阻值大小的，是和电阻的体积有关系，电阻的决定式

$R=\rho \frac{L}{S}$

ρ = 为比例系数，即电阻率，单位制为欧姆/米(Ω · m)
L = 绕制成电阻的导线长度，单位制为米(m)
S = 绕制成电阻的导线横截面积，单位制为平方米(m²)

1.3 功率公式

对于电阻我们可得：

$U=IR$

我们知道功率的公式是 $P=U\times I$ ，将其带入可得：

$P=I^{2}R$

1.4 单位换算与位数标注

$1K\Omega =1000\Omega = 10^{3}\Omega$

贴片电阻三位数代表 5% 精度，如：

$103=10\times 10^3=10K\Omega$

四位数则达到 1% 精度：

$1002=10\times 10^2=10K\Omega$

小数则是R代表小数点：

$R12=0.12\Omega$ ； $R12=0.12\Omega$

1.5 串联和并联

串联和并联和拼接出指定的电阻值

1.4.1 串联

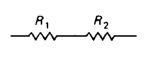
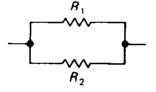
串联的电阻阻值是简单的叠加：

$R=R_{1}+R_{2}$

并联公式则是：

$R=\frac{R_{1} R_{2}}{R_{1}+R_{2}}$ 或 $R=\frac{1}{\frac{1}{R_{1}}+\frac{1}{R_{2}}}$

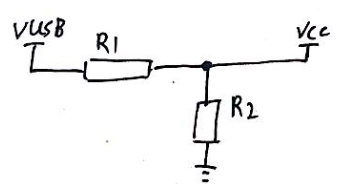
1.6 分压

分压虽然比较简单，但是还是讲解一下。

分压公式如下：

$V_{CC} = V_{USB} \cdot \frac{R_2}{R_1 + R_2}$

$\frac{V_{CC}}{V_{USB}} = \frac{R_2}{R_1 + R_2}$

二、电阻参数

2.1 标称阻值

电阻值，没什么好说的

2.2 封装

我们常说的01005、0201、0402、0603、0805等封装，是英制代码 (inch)，也叫 EIA (美国电子工业协会) 代码，还有一个是公制代码 (mm)。

英制 0603 封装表示:长度为 0.06 inch，宽度为 0.03 inch (1inch=1000mil) 公制 1608 封装表示长度1.6mm，宽度0.8mm

2.3 额定电压

额定电压：在额定环境温度下，可以对电阻持续施加的直流电压，这个叫做电阻的额定电压。

过载电压：电阻瞬间能通过的最大电压，这个时间很短，一般可能是毫秒级别，有的电阻规格书会写。

下表为普通厚膜电阻的不同封装尺寸下的工作电压、过载电压、以及介质耐压：

封装(英制)	工作电压(V)	过载电压(V)	介质承受电压(V)
0075	10	25	25
0100	15	30	30
0201	25	50	50
0402	50	100	100
0603	75	150	150
0805	150	400	500
1206	200	500	500
1210	200	500	500
1218	200	500	500
2010	200	500	500
2512	200	500	500

比如在一个电路中，电阻两端压差在 30V，那么我们至少要选一个 0402 的电阻。

3.4 额定电流

额定电流：在额定环境温度下，可以对电阻持续施加的直流电流，这个叫做电阻的额定电流。

下表为普通厚膜电阻的不同封装尺寸的电流承载能力：

封装(英制)	工作电压(A)	最大电流(A)
0075	0.5	1
0100	0.5	1
0201	0.5	1
0402	1	2
0603	1	2
0805	2	5
1206	2	10
1210	2	10
1218	6	10
2010	2	10
2512	2	10

3.5 精度

一般有 0.1%、1%，5%，10%，15%、25% 等，一般精度越高价格也越高。有些场合需要使用高精度的电阻。

其中精度所代表的字母如下：

L=±0.01%	P=±0.02%	W=±0.05%	B=±0.1%
C=±0.25%	D=±0.5%	F=±1%	G=±2%
J=±5%	K=±10%	M=±20%	N=±30%

3.6 额定功率

如有两个10Ω的电阻，一个为100W，另外一个是10W，由功率的公式：P=I^2×R，第一个电阻可以流过的最大电流为3.16A，第二个电阻可以流过的最大电流为1A。

下面是常见贴片电阻封装和功率等效关系，大功率还是要用直插式的：

下表为普通厚膜电阻的不同封装尺寸的承载功率能力：

封装(英制)	功率
0402	1/16W
0603	1/10W
0805	1/8W
1206	1/4W
1210	1/3W
1812	1/2W
2010	3/4W
2512	1W

3.7 温度系数

温度系数的单位为 PPM (百万分率)，一般的电阻阻值会随温度的上升而上升，比如现在有两个阻值都为100kΩ的电阻，电阻 1 的温度系数为 20PPM，电阻 2 的温度系数为 200PPM，当温度每升高 1℃，电阻1的阻值要增大 2Ω，电阻2的阻值要增大 20Ω。

5ppm/℃ 的意思就是：温度每变化 1℃，电压偏离其标称电压值的百万分之五。

在芯片手册中基本都会讲到温度系数，如下图所示为某款电阻的温漂范围：

三、高频特性

我们大部分情况下，电阻都是用在低频，低频考虑的东西很少，电阻就是一个电阻。

在低频电路中，可以理解电阻是一个理想态，只有电阻。

但在高频电路中，需要考虑电阻的实际等效模型，它是会有 Cp 和 Lp 这两个寄生参数，寄生并联电容和寄生串联电感。

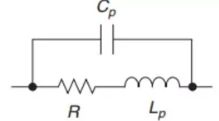
$Cp$ = 寄生并联电容 $C$
$Lp$ = 寄生并联电感 $L$

我们可知电阻、电容和电感的阻抗表达式分别是：

电阻 $R$	$Z=R$
电感 $L$	$Z=j\omega L$
电容 $C$	$Z=\frac{1}{j\omega C}$

$j$ = 虚数单位，表示相位差 90°
$\omega$ = 电压的角频率
$L$ = 电感量 (亨)
$C$ = 电容量 (法)

根据这个实际的等效模型，实际电阻的等效阻抗并不是 $R$ ，而是：

$Z=\frac{Z_{1}Z_{2}}{Z_{1}+Z_{2}}$

现在：

$Z_{1}=R+j\omega L$

$Z_{2}=\frac{1}{j\omega C}$

所以最终的阻抗公式可得：

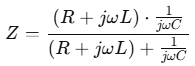
$j$ = 虚数单位，表示相位差 90°
$\omega$ = 电压的角频率
$L$ = 电感量 (亨)
$C$ = 电容量 (法)

整理后可得：

$j$ = 虚数单位，表示相位差 90°
$\omega$ = 电压的角频率 (rad/s)
$L$ = 电感量 (H)
$C$ = 电容量 (F)

这里面有两个频率点，决定了这个电阻到底呈现什么属性。

f1 为RC 滤波器截止频率点。f2 为容抗和感抗相等频率点。

四、应用案例

4.1 限流电阻

在图中，R50 起到限流作用，其中经过 D6 电流为 (3.3V - 2V)/470Ω = 0.0027A = 2.7mA。其中减去的 2V 为发光二极管压降。

R51 则是限制三极管 Q2 电流，使其工作在饱和状态。

4.3 检测电流电阻

我们测量 RS1 两端电压差后根据欧姆定律即可测量出电流。

对于 1 毫欧采样电阻可得公式：

$I=\frac{U}{0.001}$

$I$ = 电流 (A)
$U$ = 测流电流两端压差 (V)

或者另一种形式：

$I=U\times 1000$

$I$ = 电流 (A)
$U$ = 测流电流两端压差 (V)

4.2 恒流电阻

供电端电压是120mV，我们除电阻即可得到一个恒流。

4.3 取样电阻

根据欧姆定律，4mA*150 Ω 等于0.6V，供 ADC 采样。

4.4 阻抗匹配电阻

4.5 上拉电阻

R4，R5，上拉电阻，使引脚默认为高电平。

4.6 作为传感器的电阻

比如热敏电阻，热电阻，光敏电阻，湿敏电阻，压敏电阻等。

这里简单举例热敏电阻，用途是工业测温，一般有 PT20、PT100、PT1000，CU50 等。

热敏电阻分为 NTC 和 PTC，前者随着温度的上升电阻变小，后者随着温度的上升电阻变大。