硬件基础知识补全【三】电感

原创已于 2025-10-10 21:16:26 修改 · 1.6k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#单片机 #嵌入式硬件

于 2024-11-05 22:42:20 首次发布

硬件设计专栏收录该内容

10 篇文章

订阅专栏

一、电感理论

1.1 电感定义

电感定义电感定义将漆包线、纱包线或塑皮线等在绝缘骨架或磁心、铁心上绕制而成的器件，当线圈通过电流后，在线圈中形成磁场感应，感应磁场又会产生感应电流来阻碍线圈中电流的变化，这种电流与线圈的相互作用关系称为电的感抗,也就是电感，相应的器件成为电感器。

简单来说，电感将电力转化为磁场储存起来，需要释放的时候又将磁场转化为电能输出。

在电容能量未饱和下，磁畴排列是无规律的。

通电后根据楞次定律得知，磁畴逐渐同一方向，储存能量。

1.2 换算关系

亨利 ( $H$ ) 单位很大，通常使用 $mH$ 、 $\mu H$

$1H=1000mH=10^6\mu H=10^9\mu H$

1.3 定义式

$L=\frac{\mu N^{2}A}{l}$

$L$ = 电感值 (H)
$\mu$ = 介质的磁导率 (H/m)
$N$ = 线圈匝数
$l$ = 磁路长度 (m)
A = 线圈横截面积 (m²)

同样的，定义式有另一种形式：

$L=\frac{\Phi }{I}$

$\Phi$ = 磁通量
$I$ = 电流

其中磁通量定义如下：

$\Phi =BA=\mu HA$

$\Phi$ = 磁通量，穿过某个面积的磁力线总量 (Wb)
$B$ = 磁感应强度，单位面积上磁通量的密度 (T)
$\mu$ = 磁导率，材料对磁场的“传导能力” (H/m)
$H$ = 磁场强度，电流或磁源在空间产生的磁场“强度” (A/m)
$A$ = 面积，被磁场穿过的面积 (m²)

磁场强度公式如下：

$H=\frac{NI}{l}$

$H$ = 磁场强度，电流或磁源在空间产生的磁场“强度” (A/m)
$N$ = 线圈匝数
$l$ = 磁路长度 (m)

磁感应强度公式如下：

$B=\mu H=\mu \frac{NI}{l}$

$B$ = 磁感应强度，单位面积上磁通量的密度 (T)
$\mu$ = 磁导率，材料对磁场的“传导能力” (H/m)
$H$ = 磁场强度，电流或磁源在空间产生的磁场“强度” (A/m)
$\mu$ = 磁导率，材料对磁场的“传导能力” (H/m)
$N$ = 线圈匝数
$I$ = 电流
$l$ = 磁路长度 (m)

磁通量公式如下：

$\Phi=BA=\mu \frac{NIA}{l}$

$\Phi$ = 磁通量，穿过某个面积的磁力线总量 (Wb)
$B$ = 磁感应强度，单位面积上磁通量的密度 (T)
$A$ = 面积，被磁场穿过的面积 (m²)
$\mu$ = 磁导率，材料对磁场的“传导能力” (H/m)
$N$ = 线圈匝数
$I$ = 电流
$l$ = 磁路长度 (m)

1.4 感抗公式

$X_{L}=2\pi fL$

$X_{L}$ = 电感的交流感抗 (Ω)
$f$ = 交流信号的频率 (Hz)
$L$ = 电感量 (H)

电容是通交阻直，电感的特性的则是隔交通直。与电容是相反的。容抗和感抗的性质几乎正好相反，而电阻的电阻则处在这这两个极端之间。

感抗与电感的大小的频率成正比，也就是说，在同频下，电感越大，感抗越大；在同电感下，频率越大，感抗越大。

1.7 电感的实际等效模型

理想的电感阻抗模型就是我们刚才提到的感抗模型：

$X_{L}=2\pi fL$

$X_{L}$ = 电感的交流感抗 (Ω)
$f$ = 交流信号的频率 (Hz)
$L$ = 电感量 (H)

但实际上，电感等效模型如下：

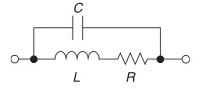
我们可知电阻、电容和电感的阻抗表达式分别是：

电阻 $R$	$Z=R$
电感 $L$	$Z=j\omega L$
电容 $C$	$Z=\frac{1}{j\omega C}$

$j$ = 虚数单位，表示相位差 90°
$\omega$ = 电压的角频率
$L$ = 电感量 (亨)
$C$ = 电容量 (法)

根据这个实际的等效模型，实际电阻的等效阻抗并不是 $R$ ，而是：

$Z_{\text{real}} = \frac{j\omega L + R}{(1 - \omega^2 L C) + j\omega R C}$

$Z_{\text{real}}$ = 电路的总阻抗(Ω)
$R$ = 电阻量 (Ω)
$L$ = 电感量 (H)
$C$ = 电容量 (C)
$\omega$ = 电压的角频率 (rad/s)
$j$ = 虚数单位，表示相位差 90°

这是根据并联电阻公式得到的：

$Z=\frac{Z_{1}Z_{2}}{Z_{1}+Z_{2}}$

从下图可以看出，理想的电感的阻抗是随着频率的增加而变大的。

等效电感的阻抗呈一个倒 V 型，正好和电容相反，倒 V 的最高点称为电感的自谐振点。

当系统阻尼 R 提供的衰减不足时，容抗和感抗相互抵消，能量在 LC 来回传递，这就是谐振。

频率低于自谐振频率SRF时，电感感抗随着频率增加而增加。
频率等于自谐振频率SRF时，电感感抗达到最大。
频率高于自谐振频率SRF时，电感感抗随着频率增加而减少。

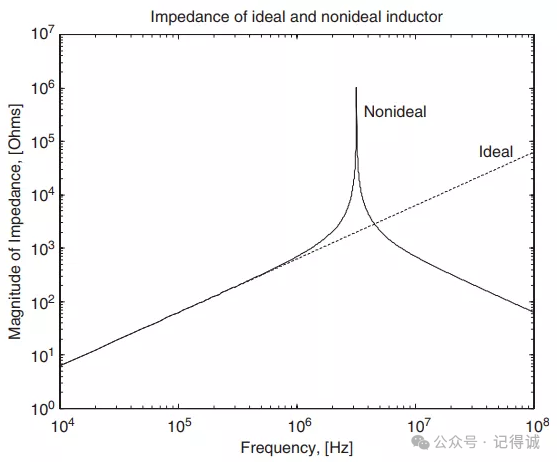
“Impedance of ideal and nonideal inductor” —— 理想与非理想电感的阻抗特性。

横轴 (Frequency, Hz)：频率，范围从 $10^4$ 到 $10^8$ Hz。
纵轴 (Magnitude of Impedance, Ohms)：阻抗的幅值，单位欧姆 (Ω)
虚线 (Ideal)：代表理想电感
实线 (Nonideal)：代表实际电感

1.5 电感充放公式

$u=L\frac{di}{dt}$

$u$ = 电感两端的电压 (V)
$L$ = 电感量 (H)
$i$ = 线圈中的电流 (A)
$\frac{di}{dt}$ = 电流随时间的变化率 (A/s)

其中 $\frac{di}{dt}$ 是电流和时间的导数，根据这个公式，电压 U 与电流变化率成正比，这意味着电流变化越快，电压就越大。

电感的电流也是不能跳变的，因为根据这个公式来看，电流跳变后导数会趋近无穷，也就是电压会无穷大。

1.6 电容和电感的电流方向

在切换充放状态下，我们可以看到电感的电流的方向是不会改变的，而电容的电流方向颠倒了，这也是容性和感性最大的区别。

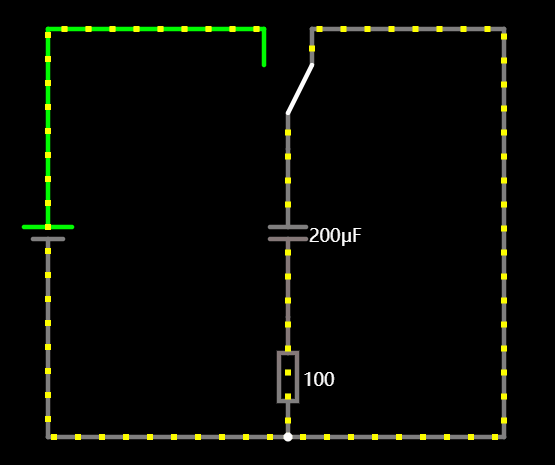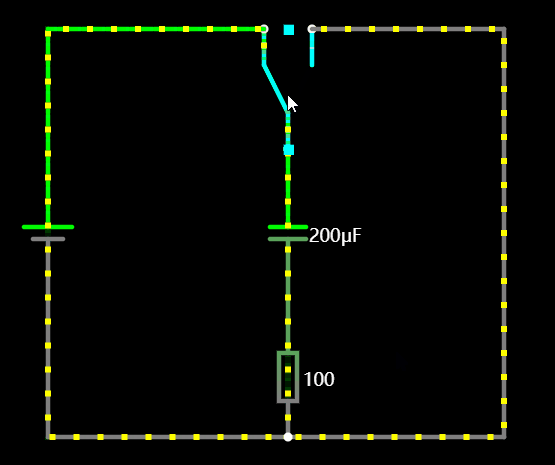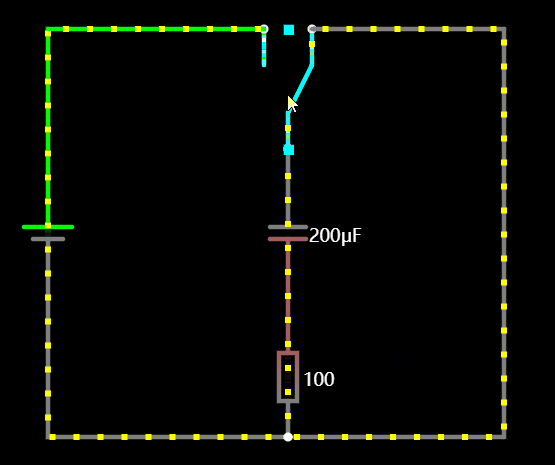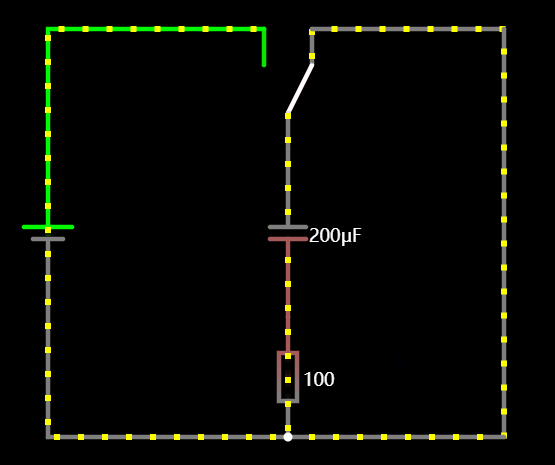
1.7 直流叠加特性

随着电流的增加，电感值呈现下降的性质，叫做电感的直流重叠特性。电流大到一定程度，达到磁饱和状态，此时电感失去电感量，电流立即增大，烧毁电感。在使用中一定要避免磁饱和现象出现。

所以一般规格书中会有 Isat 电流，电感饱和电流，电感感值下降 30% 时所容许的直流电流，实际使用过程中，是不能超过 Isat 值的。

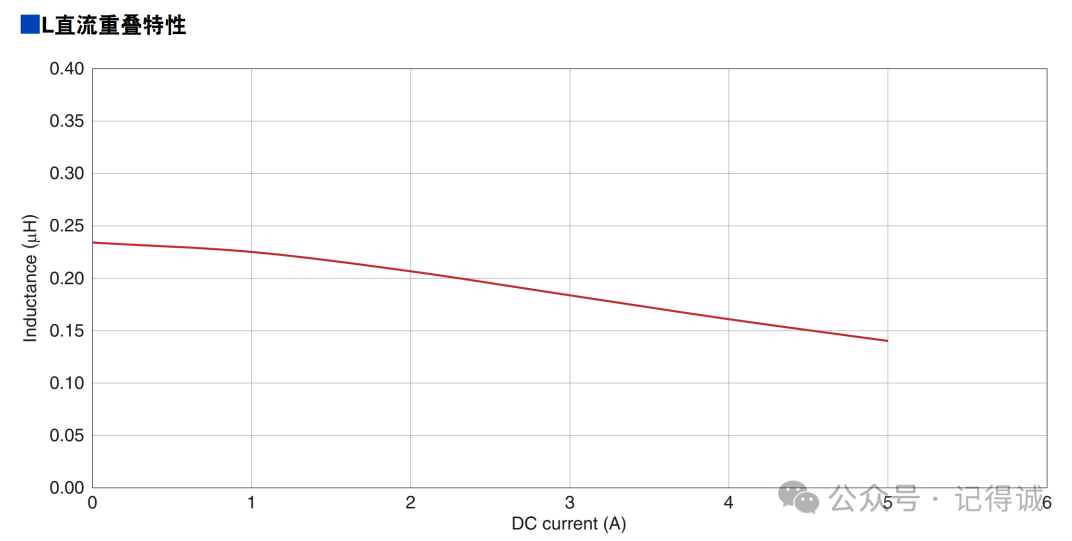
因为直流重叠特性的存在，电感的使用其实也是需要降额使用的。这个特性类似电容的直流偏压特性。

1.8 频率特性

电感和电容一样，有其频率特性曲线 (频率和电感的曲线)，有一定的频率使用范围，具体可以看下面的电感实际等效模型章节。下图是某电感规格书中给出的频率特性曲线。

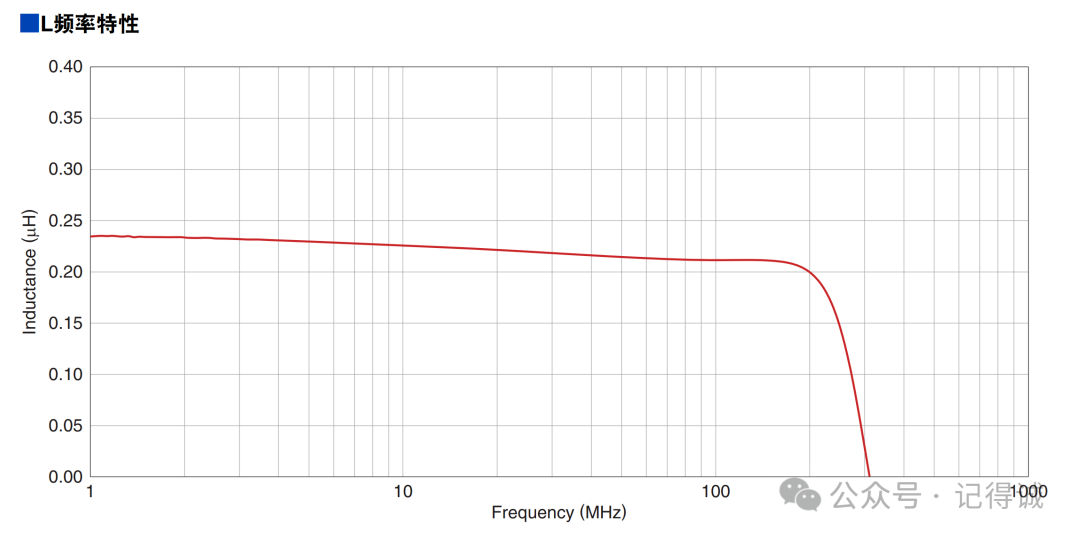
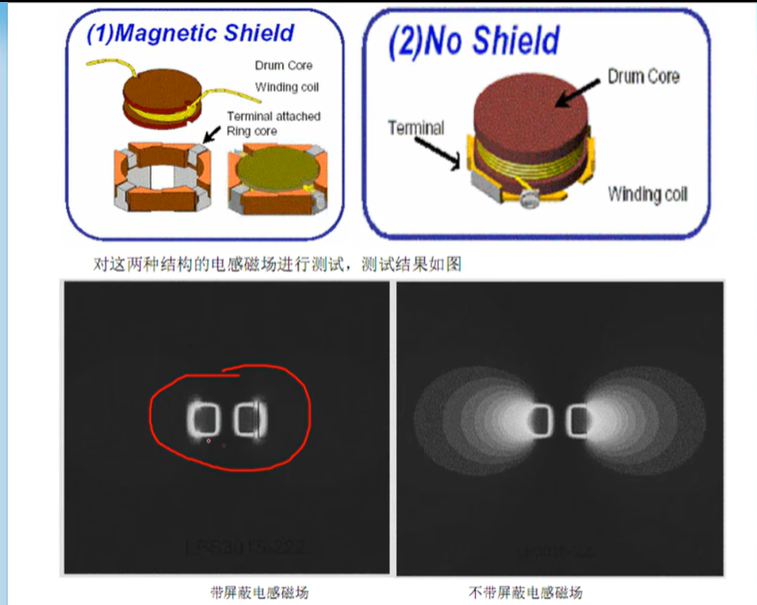
1.7 屏蔽电感和非屏蔽电感

非屏蔽电感会造成电子干扰问题，屏蔽磁场一般是采用导磁材料将电感封闭在内，电感的N极和S极产生紧密耦合，磁场在中国导磁材料内形成回路。

二、参数

我们用「功率电感 - 顺络 SWPA系列」进行参数解读

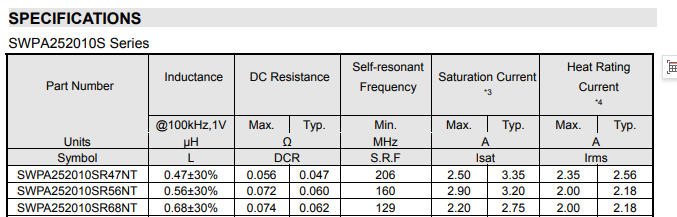
重要参数有：容量与精度 (L)、直流电阻 (DCR)、自谐振频率 (S.R.F)、通流能力 (Irms)、饱和电流 (Isat)。我们按照从左到右顺序解读：

2.1 感值 (Inductance)

感值，一般误差有 10% 或者 20%，测试条件是 1MHz 频率。

2.2 直流电阻 (DCR)

电感的直流电阻值，可以理解为寄生电阻参数，由绕线圈数和线的直径决定。一般绕电感的线越粗DCR 越小，开关电源中为了提高效率可以采用 DCR 比较小的电感。

一般情况下：

电感感值相同，尺寸越小，DCR越大。
电感尺寸相同，感值越大，DCR越大。
电感感值相同，有磁屏蔽的电感，DCR 小于没有磁屏蔽的电感。

2.3 自谐振频率 (S.R.F)

由于电感中的寄生电容，电感和自身的寄生电容有谐振频率，这个频率处电感阻抗最大，超过谐振频点阻抗开始下降，呈现容性。同电容一样，只有在特定的频率下，才能发挥电感的特性，按照经验值，SRF 一般是信号频率的 10 倍，此时的电感特性发挥的比较好。

2.4 饱和电流 (Isat)

电感饱和电流，电感感值下降 30% 时所容许的直流电流。

带有磁芯的电感，当电流增大到一定程度时，磁场强度不再增加，继续增大电流则元件的电感量将迅速下降。这个电流称为饱和电流，所以要是带磁芯的电感正常工作，不能使电流峰值超过饱和电流。不带磁芯的空心电感不存在饱和电流，其磁场随电流增大而增大，电感量不变。

2.5 通流能力 (Irms)

电感温升电流，在 20℃ 下，电感温度上升40℃所容许的直流电流。

电感由于有电阻损耗所以会发热，在热量不损坏电感的情况下，最大允许持续流过的电流。

2.5 选型方式

大多数情况根据手册选型即可，我们一般要关注感值，lrms，DRC 这些参数符合我们期望的电感电气属性即可。

三、应用案例

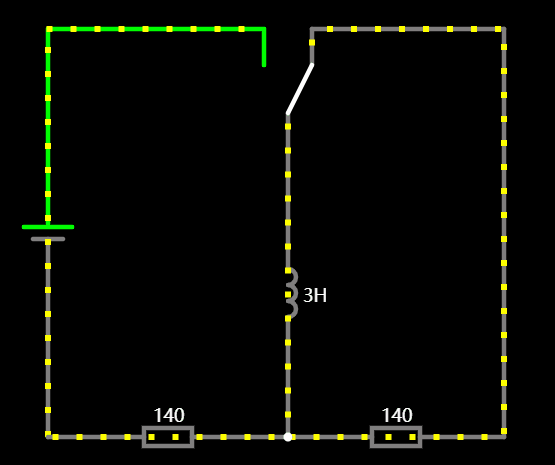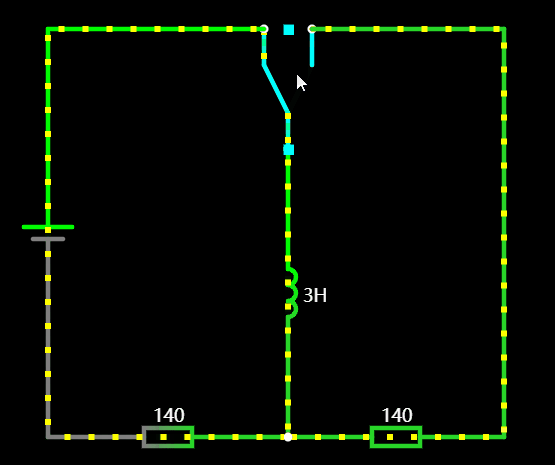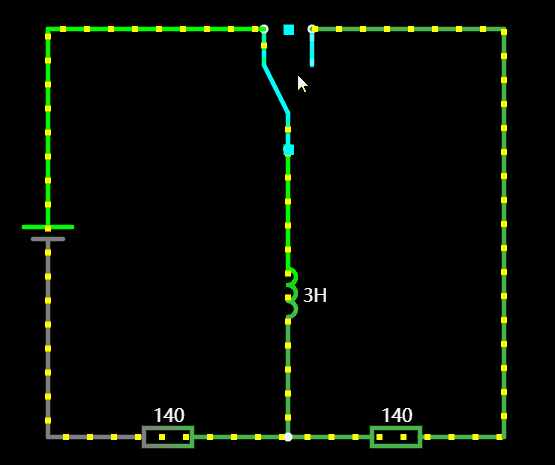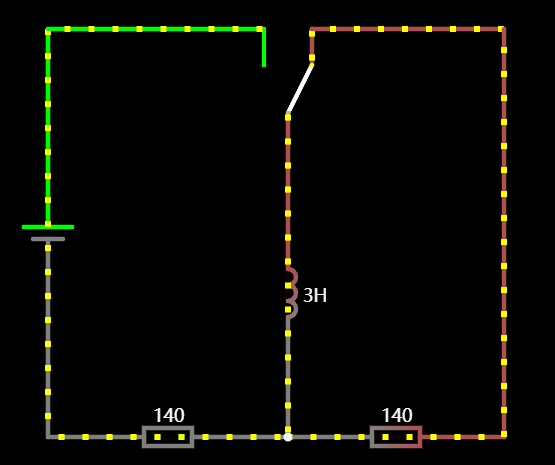
3.1 BUCK 降压电路

也称开关降压电源，通过不断开关电源，利用了在断流后电感电流方向不变的原理，其中电容是用于储能，如果我们去掉电感，会导致稳压波纹变得很大。

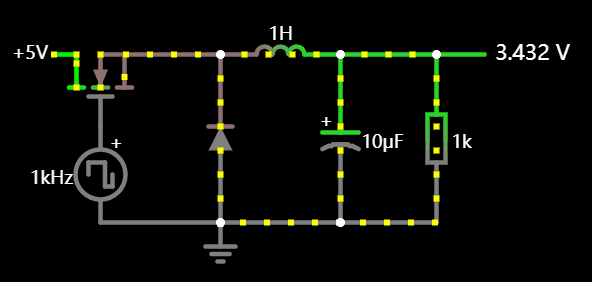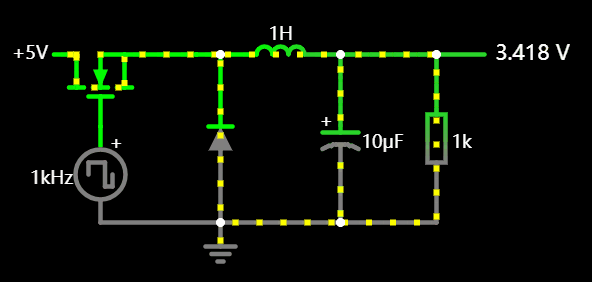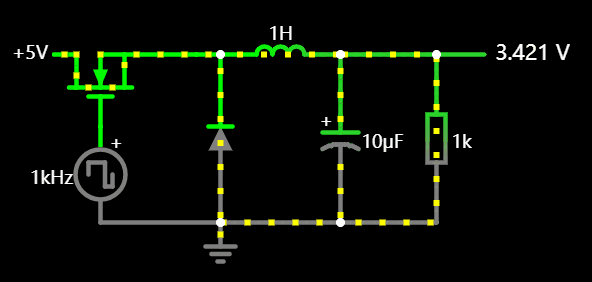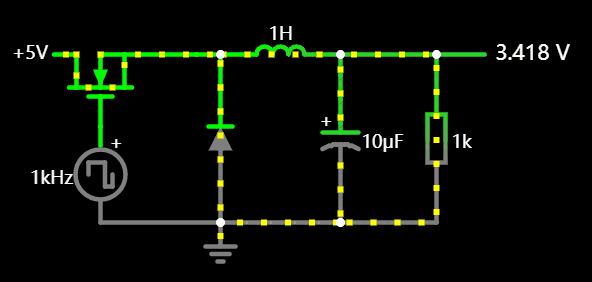
原理图应用：

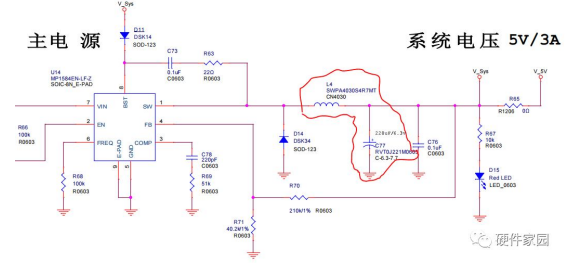
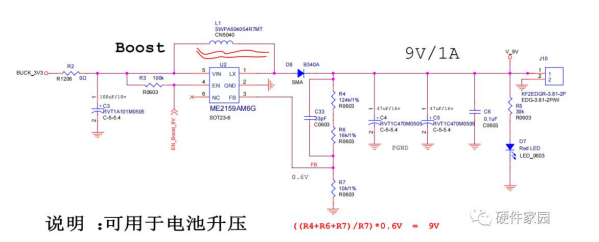
3.2 BOOTST 升压电路

根据电感充放公式：

$u=L\frac{di}{dt}$

$u$ = 电感两端的电压 (V)
$L$ = 电感量 (H)
$i$ = 线圈中的电流 (A)
$\frac{di}{dt}$ = 电流随时间的变化率 (A/s)

一旦电流 i = 0，电感自身就提升电压以维持电流，我们正是利用这一点制作的 BOOTST 升压电路。

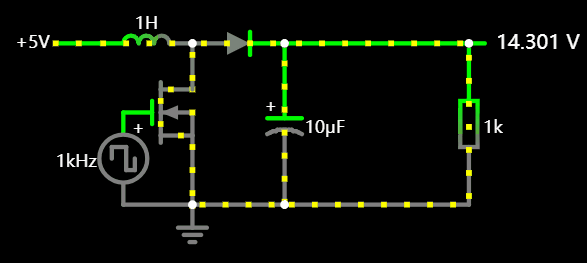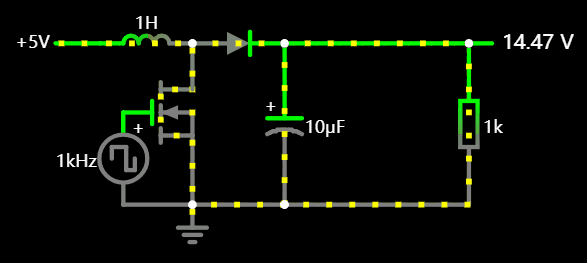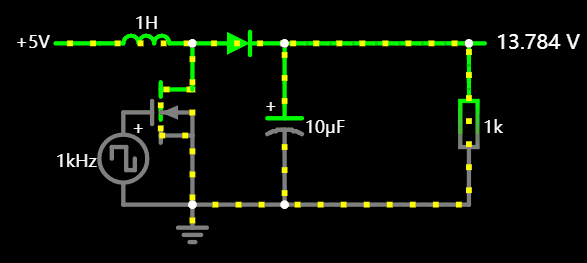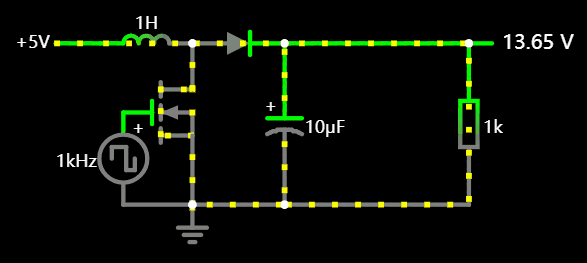
原理图应用：