分数阶互感：分析与设计

分数阶互感：分析与设计

1. 引言

近年来，由于分数阶微积分在描述许多现实现象的动力学行为方面比整数阶动力系统具有更高的精确性，因此被广泛应用于建模。这种额外的灵活性主要源于分数阶系统具有无限记忆的特性，而整数阶系统则具有有限记忆[1]。此外，由于增加了分数阶参数，在对许多应用进行建模、分析和控制时提供了更大的灵活性，例如确定非理想电容器中的电压‐电流关系 [2, 3], 、金属绝缘体溶液界面的分形行为[4],、电磁波[5],，以及最近在电路中的滤波器[6–11]和振荡器[12–14]。此外，分数阶微积分的应用已在物理学[15],、地震的非线性振荡[16],和数学生物学[17]等多个领域得到报道。

阶次为 α的分数阶导数的卡普托定义可写为如下形式[18]：
$$
aD^\alpha_t f(t) :=
\begin{cases}
\frac{1}{\Gamma(m - \alpha)} \int_0^t \frac{f^{(m)}(\tau)}{(t - \tau)^{\alpha + 1 - m}} d\tau & m - 1 < \alpha < m \
\frac{d^m}{dt^m} f(t) & \alpha = m
\end{cases}
$$
其中 $a$ 和 $t$ 分别是计算的初始时间和所需时间。对(1)式的通用分数阶导数在零初始条件下进行拉普拉斯变换得到：
$$
\mathcal{L}\left{_0D^\alpha_t f(t)\right} = s^\alpha F(s)
$$
因此，可以定义一种广义的分抗器件，其阻抗与$s^\alpha$[19]成正比，其中传统的电路元件——电容器、电阻器和电感器——分别是当阶次为 $-1$, $0$,和$1$时的分数阶元件的特例。在过去的 10年中，已提出多种有前景的实现分数阶元件的方法，这些方法基于不同的技术，如化学反应[20], 、分形结构[4],以及石墨烯材料[21]。此外，已有许多有限电路近似被提出用于建模分数阶元件，例如，针对特例Z= 1/(Cs0.5)的有限元近似已在[22]中报道。该有限元近似依赖于通过半无限电阻‐电容树来模拟分数阶电容的可能性。这一技术随后由[23–25]的作者推广至任意阶次。

另一方面，传统的互感耦合电路（MCCs）在仪器仪表、通信、控制系统、信号处理和建模[26–28]中具有广泛的应用。它们还可用于模拟滤波器，特别是用于在参差调谐滤波器中替代磁性变压器[29, 30]。在前述模块中使用MCC提高了设计灵活性和系统性能。MCC的特征参数包括初级电感、次级电感、互感和耦合系数。MCC由以下阻抗矩阵[31]表征：
$$
\begin{bmatrix}
V_1 \ V_2
\end{bmatrix}
=
s
\begin{bmatrix}
L_{11} \pm M & M \
M & L_{22} \pm M
\end{bmatrix}
\begin{bmatrix}
I_1 \ I_2
\end{bmatrix}
$$
其中$L_{11}$,$M$和$L_{22}$分别为初级电感、互感和次级电感。从图1(a)所示的MCC T型模型来看，MCC依赖于使用电感器来实现互感。尽管存在性能非常好的电感器或电容器，但它们通常表现出分数阶行为，其分数阶次为$0.999 \leq \alpha \leq 0.9999$[32, 33]。此外，在射频（RF）应用中，这种分数阶值可能更小[34]。分数阶电容器和电感器的物理原型在[3,35]中有所展示。因此，有必要提出基于电感器分数阶模型的MCC分析方法。在这种情况下，便产生了一个新概念，即分数阶互感耦合电路（FMCCs）。由于设计参数的增加，FMCC可用来替代整数阶互感，从而提高设计自由度。

本文的结构如下：第2节讨论了分数阶互感（FMI）的概念。接着，第3节提出了一个 FMCC。第4节介绍了基于FMI和FMCC的应用，如双调谐滤波器和阻抗匹配。最后，第5节给出了本文的结论。

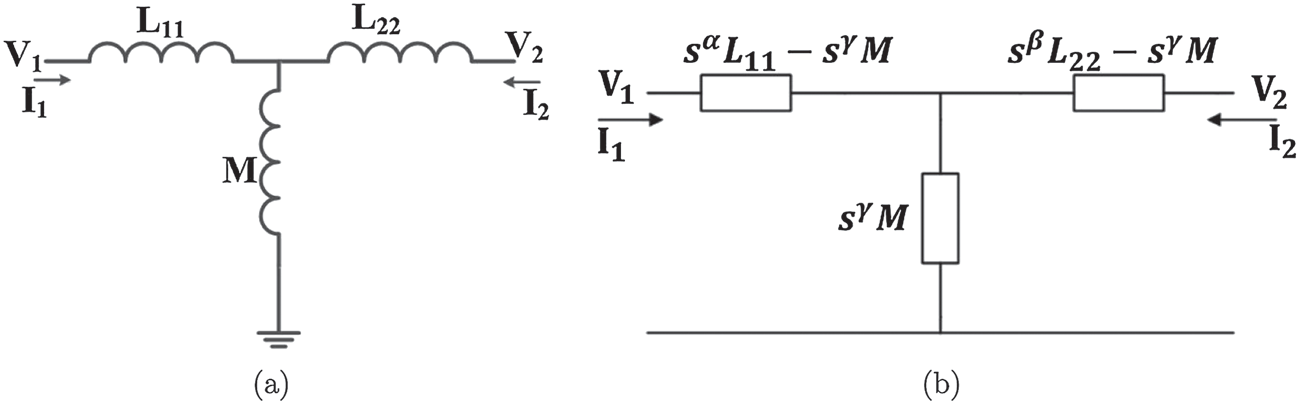整数阶互感的T型模型和(b) 所提出的分数阶互感的T型模型)

2. 提出的分数阶互感

传统的MCC（磁耦合电路）是一个无损耗网络，这在实际中并不现实；因此，可以引入分数阶参数来加入损耗项，这些损耗项已被Coilcraft报告[34,36]证明具有频率依赖性。为了推广，假设初级和次级电感器分别为不同的分数阶 $\alpha$、$\beta$。因此，在这种情况下，互感不再对称，且互感可视为具有分数阶 $\gamma$。于是，每个分数阶电感器中的感应电动势应表示为
$$
emf_1 = v_1 = L_{11} \frac{d^\alpha i_1}{dt^\alpha} \pm M_{12} \frac{d^{\gamma_{12}} i_2}{dt^{\gamma_{12}}}
\quad (4a)
$$
$$
emf_2 = v_2 = M_{21} \frac{d^{\gamma_{21}} i_1}{dt^{\gamma_{21}}} \pm L_{22} \frac{d^\beta i_2}{dt^\beta}
\quad (4b)
$$
然后，对(4)式进行拉普拉斯变换，FMI可以用以下阻抗矩阵方程表示：
$$
\begin{bmatrix}
V_1 \ V_2
\end{bmatrix}
=
\begin{bmatrix}
s^\alpha L_{11} & s^{\gamma_{12}} M_{12} \
s^{\gamma_{21}} M_{21} & s^\beta L_{22}
\end{bmatrix}
\begin{bmatrix}
I_1 \ I_2
\end{bmatrix}
\quad (5)
$$
对于传统情况$\alpha=\beta=\gamma_{12}=\gamma_{21}= 1$，(5)式的矩阵表示了在(3)中提出的整数阶MCC的矩阵方程。(5)式的阻抗矩阵表示了所提出的FMI的行为，该FMI是传统互感的一般化形式。FMI的初级和次级电感器具有不相等的相位响应。此外，初级与次级电感器之间的耦合是不对称的。

由(5)式建模的FMI仅在对称耦合 $\gamma_{12}=\gamma_{21}=\gamma$且$M_{12}=M_{21}$的情况下，可用图1(b)所示的等效 T型电路表示。然而，虽然可以使用电阻‐电容梯形网络来近似实现分数阶电容，但采用相同的拓扑结构实现分数阶电感器却较为困难，因为它需要多个电感器[37]。因此，可将分数阶电容与通用阻抗转换电路（GIC）结合使用，以实现接地分数阶电感器，如图 2[12,38]所示。

另一方面，为了实现浮地分数阶电感器，需使用两个级联的GIC[39, 40]。因此，图2中GIC 的输入阻抗如下所示：

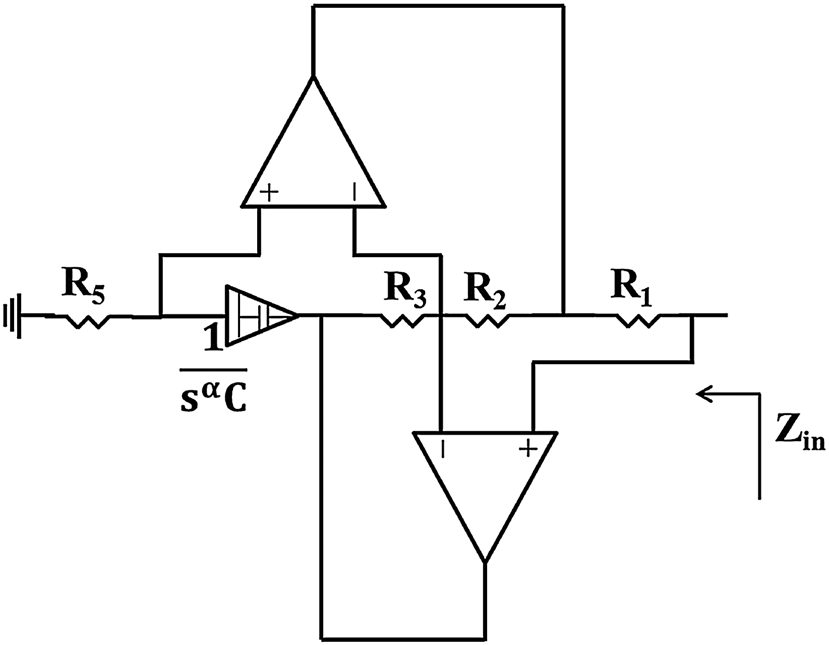
$$
Z_{in} = s^\alpha \frac{CR_1R_3R_5}{R_2}
\quad (6)
$$
From (6)，阶次为 $\alpha$的分数阶电感器的电感为 $L= CR_1R_3R_5/R_2$。

此外，对称耦合这一特殊情况下的所提出的FMI符号如图3(a)所示。为了进行仿真，图 1(b)的T型模型可以替换为图3(b)的电路。此时，阻抗矩阵变为如下形式：
$$
\begin{bmatrix}
V_1 \ V_2
\end{bmatrix}
=
\begin{bmatrix}
s^\alpha L_{11} + s^\gamma M & s^\gamma M \
s^\gamma M & s^\beta L_{22} + s^\gamma M
\end{bmatrix}
\begin{bmatrix}
I_1 \ I_2
\end{bmatrix}
\quad (7)
$$
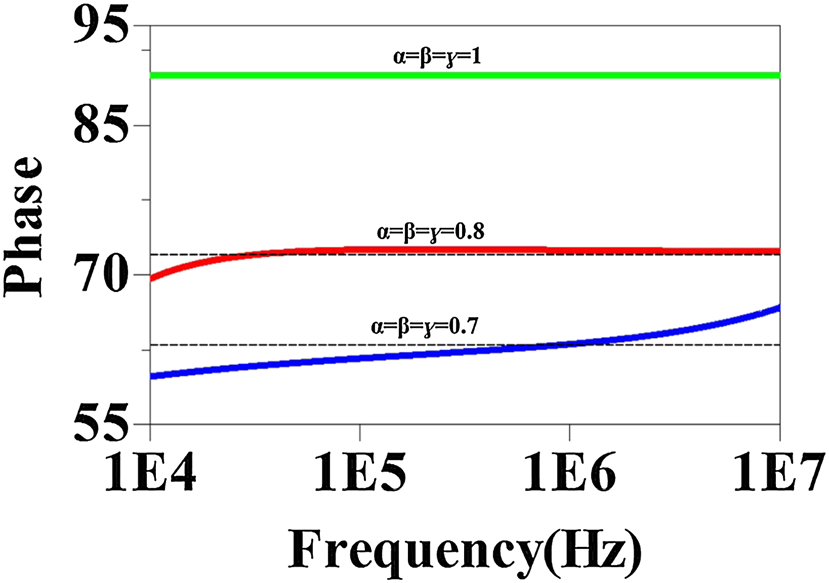
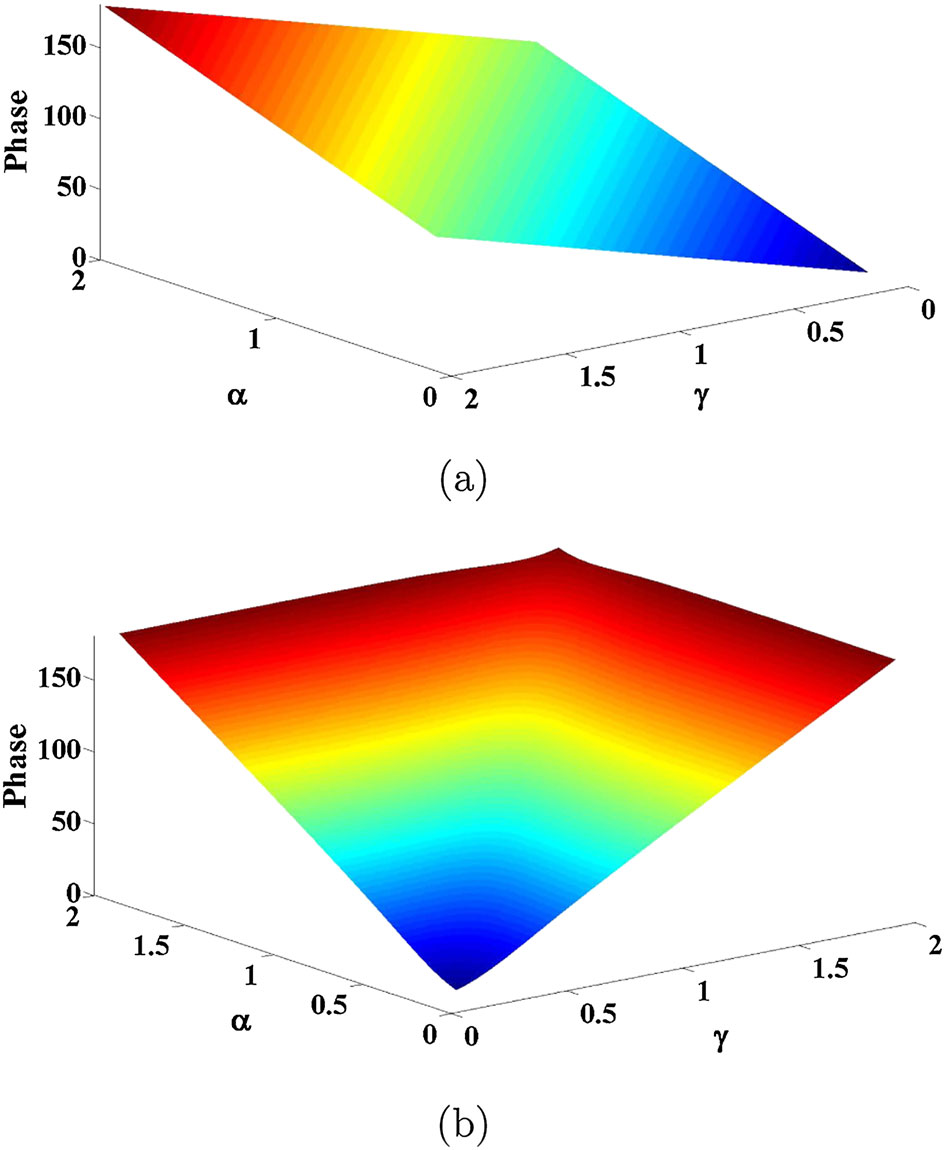
随后，对于 $\alpha=\beta=\gamma$的情况，该模型表示一个对称分数阶互感。在这种情况下，阻抗矩阵所有参数的相位为 $\alpha\pi/2$。此时相位值取决于分数阶 $\alpha$，从而增加了设计自由度。图3(b)所示 FMCC电路在不同 $\alpha$取值下的电路仿真结果如图4所示。传统情况下的相位响应为 $\pi/2$，但当电感元件被替换为分数阶元件时，相位将根据 $\alpha$的取值发生变化，如图4所示。在仿真频率范围内，仿真与理想相位响应（图4中的虚线）之间的相位误差在 $\alpha= 0.8$时为 ±3°，在 $\alpha= 0.7$时为 ±4°。这一较小的误差表明，FMCC适用于宽频带的应用。

另一个重要情况出现在 $\alpha=\beta \neq \gamma$时，此时阻抗矩阵参数的相位可使用[36]的公式计算如下：
$$
\angle Z_{11,22} =
\begin{cases}
2\tan^{-1} \left( \frac{y_{11,22}}{x_{11,22} + \sqrt{x_{11,22}^2 + y_{11,22}^2}} \right) & x > 0 \text{ or } y \neq 0 \
\pi & x < 0 \text{ and } y = 0 \
\text{Undefined} & x = 0 \text{ and } y = 0
\end{cases}
\quad (8a)
$$
$$
\angle Z_{12,21} = \frac{\gamma\pi}{2}
\quad (8b)
$$
其中
$$
y_{11,22} = \omega^\alpha L_{11,22} \sin(0.5\alpha\pi) + \omega^\gamma M \sin(0.5\gamma\pi)
\quad (9a)
$$
$$
x_{11,22} = \omega^\alpha L_{11,22} \cos(0.5\alpha\pi) + \omega^\gamma M \cos(0.5\gamma\pi)
\quad (9b)
$$
其中，$L_{11,22}$为FMI模型的初级和次级电感。实际上，阻抗参数$Z_{11}$和$Z_{22}$的相位响应与实际电感模型[41, 42]的相位响应相同。这是预料之中的，因为这些阻抗参数代表了互感电感器的阻抗。另一方面，$Z_{12}$和$Z_{21}$表示两个电感器之间的耦合，并不代表一个实际的电感器。通过这一简单分析可知，即使分数阶不同，式(7)的阻抗矩阵仍能表示FMCC的行为。此外，分数阶模型可以通过改变分数阶的值($\alpha, \gamma$)来控制FMCC的寄生元件。同时，相位是电感值($L_{11,22}$和$M$)以及工作频率的函数，这增加了设计自由度，如图5(a)和(b)中在不同频率点所示。由 (8a)可知，分数阶($\alpha, \gamma$)的影响是对称的，如图5所示。对于特殊情况$\alpha=\gamma= 0$，元件趋向于表现为电阻，因为此时相位等于零。

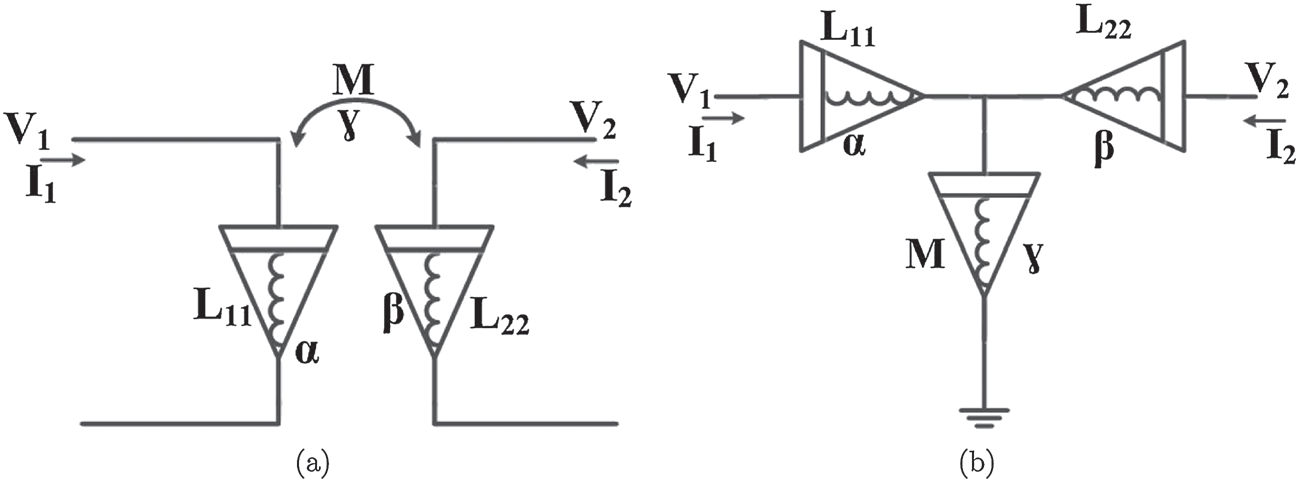分数阶互感的建议符号和(b) 分数阶互感的等效T型模型)

$\omega_o = 1$ rad/s 和 (b) $\omega_o = 1$ krad/s)

正如预期。另一方面，对于 $\alpha=\gamma= 1$，这些元件表现为纯电感器，且相位等于 $\pi/2$，如图5所示。然而，使用分数阶元件时，这并非实现纯电感行为的唯一条件。根据(8a)，满足纯电感行为的条件如下：
$$
\omega^{\alpha-\gamma} {11,22\text{pure}} = -\frac{M \cos(0.5\gamma\pi)}{L {11,22} \cos(0.5\alpha\pi)}
\quad (10a)
$$
$$
y_{11,22\text{pure}} = \omega^\alpha_{11,22\text{pure}} L_{11,22} \sin(0.5\alpha\pi) + \omega^\gamma_{11,22\text{pure}} M \sin(0.5\gamma\pi)
\quad (10b)
$$
由(10a)可知，存在无限多种条件可获得纯电感响应。因此，对于给定的 $\alpha$值和所需频率，可通过计算得到分数阶 $\gamma$的值以满足(10a)的条件，如图6(a)所示。然后，利用(10b)计算纯电感的值，如图6(b)所示。类似地，通过将余弦函数替换为正弦函数，可得到纯电阻响应的条件及其值，如下所示：
$$
\omega^{\alpha-\gamma} {11,22\text{pure}} = -\frac{M \sin(0.5\gamma\pi)}{L {11,22} \sin(0.5\alpha\pi)}
\quad (11a)
$$
$$
x_{11,22\text{pure}} = \omega^\alpha_{11,22\text{pure}} L_{11,22} \cos(0.5\alpha\pi) + \omega^\gamma_{11,22\text{pure}} M \cos(0.5\gamma\pi)
\quad (11b)
$$
值得注意的是，相位响应是工作频率的函数，这与电路元件的实际响应[34]相符。

最后，更一般的情况是 $\alpha \neq \beta \neq \gamma$表示分数阶互感，但阻抗矩阵参数$Z_{11}$、$Z_{22}$的相位不同。此时可认为该互感为不对称的，从而定义了一种新的非对称互感概念。阻抗参数$Z_{11}, Z_{22}$的相位方程与(8a)类似，但在分别为各元件采用适当的分数阶 $\alpha$、$\beta$和适当的电感值$L_{11}, L_{22}$之后。

图3(b)所示的分数阶互感模型的电路仿真在不同分数阶情况下如图7所示。当$(\alpha, \beta, \gamma)=(1,1,0.7)$时，结果如图7(a)所示，其中阻抗参数$Z_{12,21}$的相位响应接近于 63°，且其频率影响可忽略不计，符合(8b)的预期。然而，如(8a)中先前讨论的，频率对阻抗参数及$Z_{11,22}$的相位响应的影响较大。另一方面，针对不同分数阶的一般情况$(\alpha, \beta, \gamma)=(0.5,1.4,0.4)$的仿真为

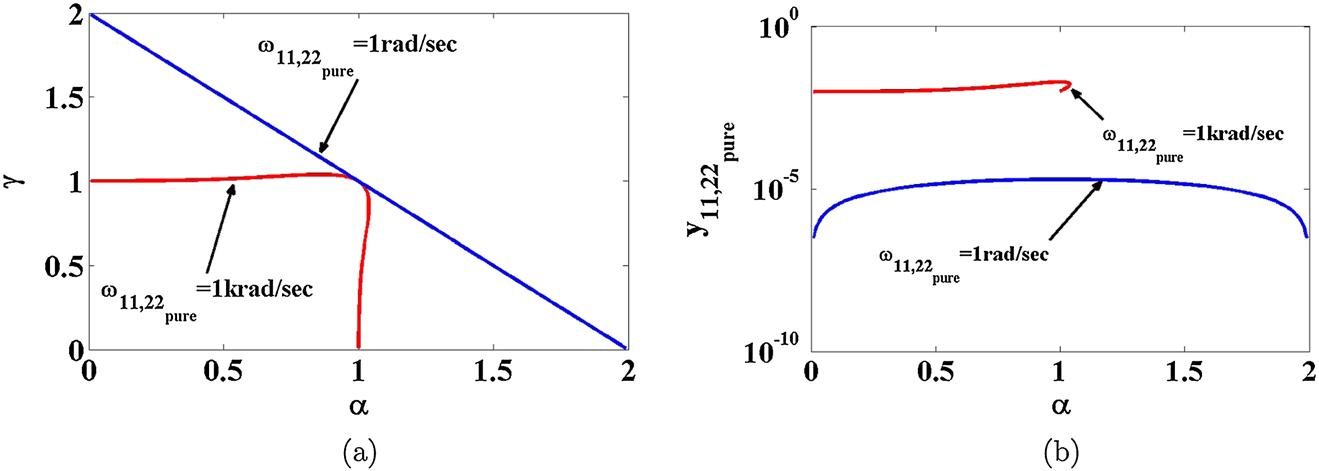在不同频率下满足(10a)条件的 $\gamma$值，其中$L_{11,22} =M = 10\mu H$；(b) 在不同频率值下，纯电感值随分数阶次 $\alpha$的变化情况，其中$L_{11,22} =M = 10\mu H$)

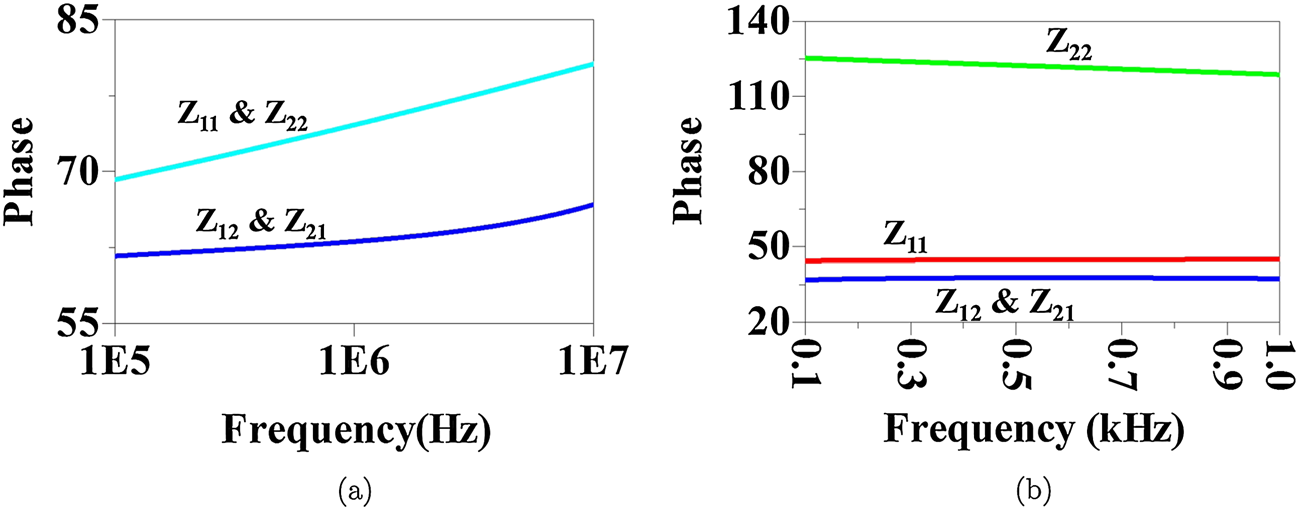$\alpha= \beta= 1$和 $\gamma= 0.7$；(b) $\alpha= 0.5$、 $\gamma= 0.4$和 $\beta= 1.4$)

分数阶互感：分析与设计

3. 等效电路

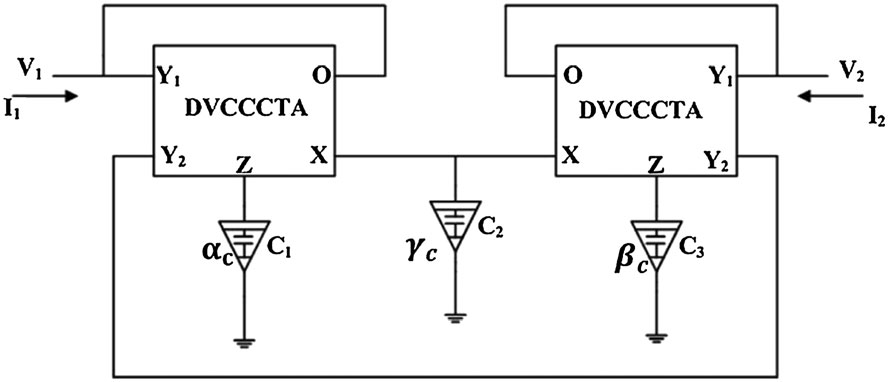
在本节中，基于差分电压电流控制传送跨导放大器（DVCCCTA）的FMI等效电路如图8所示。该FMI本质上是浮地的。该等效电路由两个DVCCCTA和三个阶次为($\alpha_c, \gamma_c, \beta_c$)的接地分数阶电容器组成。DVCCCTA的端口关系可表示如下：
$$
\begin{bmatrix}
I_{Y1} \ I_{Y2} \ V_X \ I_Z \ I_O
\end{bmatrix}
=
\begin{bmatrix}
0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 \
1 & -1 & R_X & 0 & 0 \
0 & 0 & 0 & 1 & 0 \
0 & 0 & 0 & 0 & g_m
\end{bmatrix}
\begin{bmatrix}
V_{Y1} \ V_{Y2} \ I_X \ V_Z \ V_O
\end{bmatrix}
\quad (12)
$$
其中，$R_X$为X端口的固有电阻，$g_m$为DVCCCTA从Z端口到O端口的跨导。本文所用 DVCCCTA的电路实现如[29]所示。对图8所示FMCC等效电路进行常规分析，可得其阻抗矩阵为(13)，该矩阵与(5)中给出的一般FMI情况的阻抗矩阵相似。因此，图8的电路可实现为一种不对称耦合的分数阶互感。表I列出了(5)式中阻抗矩阵参数与图8等效电路元件之间的对应关系。图8的电路在不同条件下可实现分数阶互感的不同行为。这些响应及其必要条件汇总于表II，其中传统互感行为出现在 $\alpha_c=\beta_c= 1$和 $\gamma_c= 0$且$C_3= C_1$时，此时阻抗矩阵参数的相位响应为 $\pi/2$，如图9(a)所示。此外，当满足 $\alpha_c=\beta_c$、$\gamma_c= 0$且$C_3=C_1$时，可实现对称FMI行为。对称FMI情况下阻抗矩阵参数的相位响应如图9(b)所示。
$$
\begin{bmatrix}
V_1 \ V_2
\end{bmatrix}
=
\begin{bmatrix}
s^{\alpha_c} \frac{C_1 R_{X1}}{g_{m1}} + s^{\alpha_c - \gamma_c} \frac{C_1}{g_{m1} C_2} & s^{\beta_c - \gamma_c} \frac{C_3}{g_{m2} C_2} \
s^{\alpha_c - \gamma_c} \frac{C_1}{g_{m1} C_2} & s^{\beta_c} \frac{C_3 R_{X2}}{g_{m2}} + s^{\beta_c - \gamma_c} \frac{C_3}{g_{m2} C_2}
\end{bmatrix}
\begin{bmatrix}
I_1 \ I_2
\end{bmatrix}
\quad (13)
$$
最后，当分数阶 $\alpha_c$或$\beta_c$小于分数阶 $\gamma_c$时，在耦合点（$Z_{12},Z_{21}$）处会出现电容效应。该特性可用于阻抗匹配电路中，以补偿互感电路的电感。

表I. 阻抗矩阵参数与电路元件之间关系的摘要。

参数	与等效电路元件的关系
$\alpha$	$\alpha_c$
$\beta$	$\beta_c$
$\gamma_{12}$	$\alpha_c - \gamma_c$
$\gamma_{21}$	$\beta_c - \gamma_c$
$L_{11}$	$\frac{C_1 R_{X1}}{g_{m1}}$
$L_{22}$	$\frac{C_3 R_{X2}}{g_{m2}}$
$M_{12}$	$\frac{C_1}{g_{m1} C_2}$
$M_{21}$	$\frac{C_3}{g_{m2} C_2}$

表II. 满足所提出的分数互感的必要条件。

行为描述	必要条件
传统互感	$\alpha_c = \beta_c = 1$和 $\gamma_c = 0$和$C_1 = C_3$
对称分数阶互感	$\alpha_c = \beta_c$ 和 $\gamma_c = 0$
非对称分数阶互感	$\alpha_c = \beta_c > \gamma_c$
具有电容效应的分数互感	$\alpha_c$ 或 $\beta_c < \gamma_c$
具有电阻效应的分数互感	$\alpha_c$ 或 $\beta_c = \gamma_c$

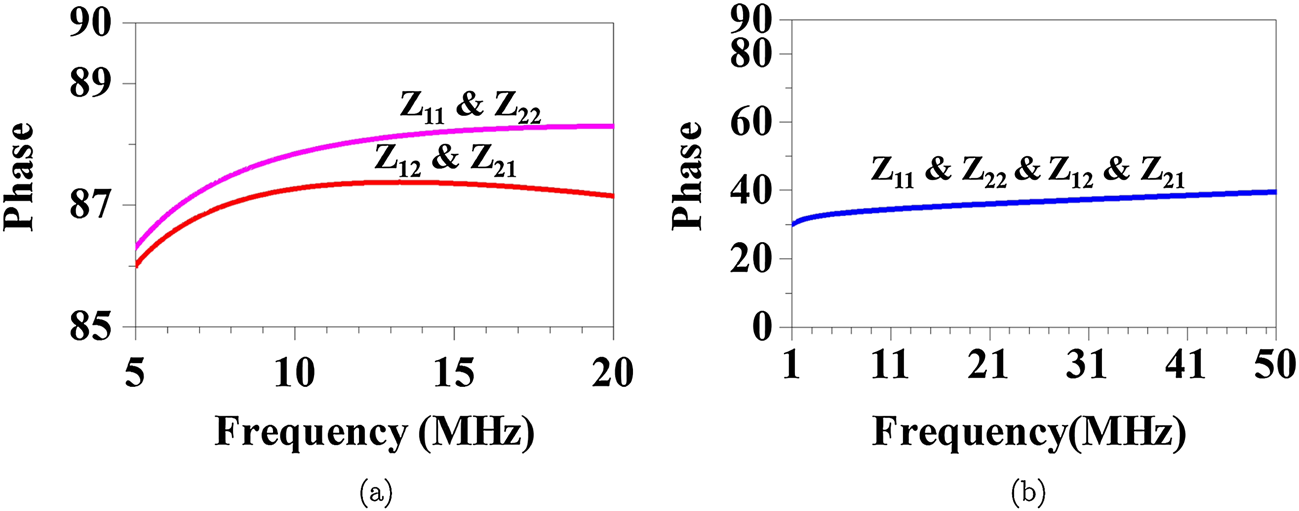$\alpha_c= \beta_c= 1$和 $\gamma_c= 0$，以及(b) $\alpha_c=\beta_c= 0.4$ 和 $\gamma_c= 0$)

4. 应用

现在，证明FMCC的可靠性非常重要。因此，本节的目的是在不同应用中使用FMCC。

4.1. 双调谐滤波器

双调谐滤波器被认为是主要基于互感的应用之一。传统的双调谐滤波器由一个串联谐振电路和一个并联谐振电路组成。因此，双调谐滤波器能够实现比传统滤波器更宽的带宽带通滤波器。因此，本节的目标是利用分数阶互感构建分数阶双调谐滤波器。双调谐滤波器的电路图如图10(a)所示，其传递函数如下所示：
$$
T(s) = \frac{V_{out}}{V_{in}} = \frac{M}{R_P C_P L_P C_S L_S} \frac{s^{\gamma_c}}{\left(s^{\alpha_c + 1} + \frac{1}{R_P C_P} s^{\alpha_c} + \frac{1}{C_P L_P}\right)\left(s^{\beta_c + 1} + \frac{1}{R_S C_S} s^{\beta_c} + \frac{1}{C_S L_S}\right)}
\quad (14)
$$
尽管式(14)中的传递函数表示一个阶次为 $\alpha_c+\beta_c+ 2$的带通滤波器，但该电路并未表现出这种响应。实际上，该电路作为两个在不同半功率频率下工作的带通滤波器运行。因此，该电路称为双调谐电路。此时，传递函数可表示如下：
$$
T(s) = \frac{a_1 s^{\gamma_1}}{s^{\alpha_c + 1} + \frac{1}{R_P C_P} s^{\alpha_c} + \frac{1}{C_P L_P}} \cdot \frac{a_2 s^{\gamma_2}}{s^{\beta_c + 1} + \frac{1}{R_S C_S} s^{\beta_c} + \frac{1}{C_S L_S}}
\quad (15)
$$
为简化起见，假设 $\gamma_1=\alpha_c$、 $\gamma_2=\beta_c$和 $\gamma_1+\gamma_2=\gamma_c$以及$a_1 \cdot a_2 = \frac{M}{R_P C_P L_P C_S L_S}$。则传递函数可重写如下：
$$
T(s) = \frac{a_1 s^{\alpha_c}}{s^{\alpha_c + 1} + \frac{1}{R_P C_P} s^{\alpha_c} + \frac{1}{C_P L_P}} \cdot \frac{a_2 s^{\beta_c}}{s^{\beta_c + 1} + \frac{1}{R_S C_S} s^{\beta_c} + \frac{1}{C_S L_S}}
\quad (16)
$$
因此，(16)式的传递函数表示两个级联的分数阶带通滤波器。因此，该滤波器的关键频率点（截止频率、最大和最小频率点以及右相位频率）可利用[7–9, 43]中提出的算法确定。于是，这些关键频率点成为分数阶 $\alpha$、$\beta$的函数，从而增加了设计自由度[7–9, 43]。实际上，基于FMI的双调谐滤波器的频率响应具有两个谐振频率，如图10(b)的数值分析所示。因此，滤波器带宽如预期般得到增加。此外，图10(b)展示了使用相同元件值但在不同分数阶下的滤波器频率响应。显然，滤波器的截止频率随分数阶的变化而变化，如前所述。

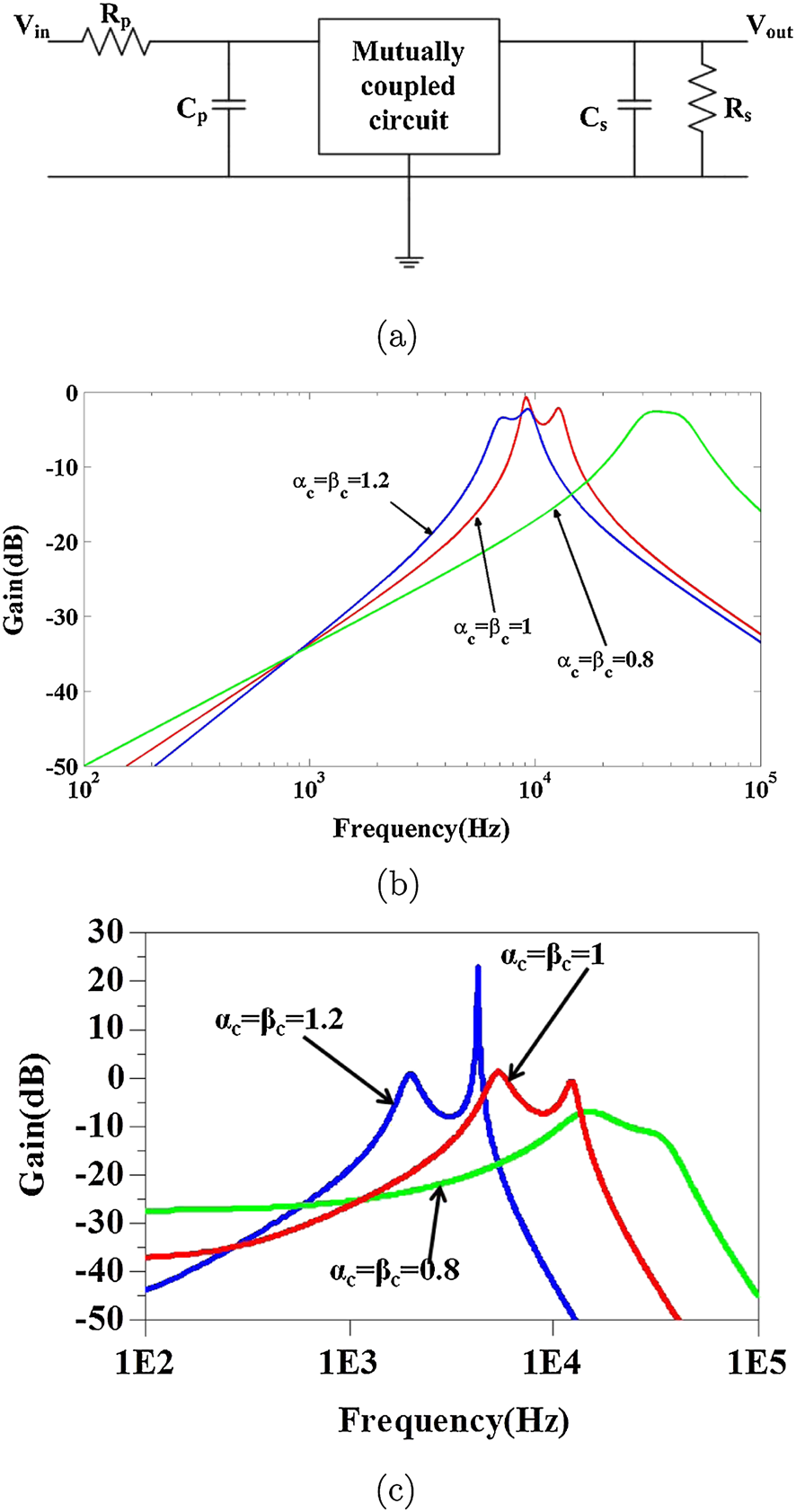使用分数阶互感耦合电路等效电路的双调谐滤波器，(b) 具有$R_P=R_s= 11$kΩ和$C_s= 20$nF、$C_P= 10$nF的双调谐滤波器的数值分析，以及(c) 双调谐滤波器$R_P= R_s= 11$kΩ和$C_s= 20$nF、$C_P= 10$nF的电路仿真)

4.2. 分数阶互感耦合电路在阻抗匹配中的应用

阻抗匹配问题是一个重要的问题，在大多数微波设计中都必须加以解决[44, 45, 31]。互感是阻抗匹配中最常用的技术之一。因此，本文提出了利用FMCC进行阻抗变换的方法。如图 11(a)所示，采用图3(b)所示FMCC的等效T型模型进行阻抗匹配分析。为了简化分析，此处讨论具有$\alpha=\beta=\gamma$的对称分数阶互感的情况。然后，通过简单的常规分析，可由(17)式计算出电路的负载阻抗。
$$
Z_{Load} = \frac{\omega^\alpha \cos(\alpha\pi) (L_{11}L_{22} + M (L_{22} + L_{11})) + Z_{source} \cos(0.5\alpha\pi) (L_{22} + M)}{L_{11} \cos(0.5\alpha\pi) + Z_{source} \omega^{-\alpha} + M \cos(0.5\alpha\pi)}
\quad (17a)
$$
$$
Z_{Load} = \frac{\omega^\alpha \sin(\alpha\pi) (L_{11}L_{22} + M (L_{22} + L_{11})) + Z_{source} \sin(0.5\alpha\pi) (L_{22} + M)}{(L_{11} + M) \sin(0.5\alpha\pi)}
\quad (17b)
$$
对于传统情况 $\alpha=\beta=\gamma= 1$，输入阻抗与负载阻抗之间的关系如下：
$$
\frac{Z_{Load}}{Z_{source}} = \frac{L_{22} + M}{L_{11} + M}
\quad (18a)
$$
$$
Z_{Load} Z_{source} = -\omega^2 (L_{11}L_{22} + M (L_{22} + L_{11}))
\quad (18b)
$$
(18a) 中的关系与众所周知的整数阶互感[31]关系相同，从而验证了(17)。然而，此情况下的谐振频率值为负，如(18b)所示。这意味着系统不稳定，需要补偿电容来消除电感效应。另一方面，根据(17)，对于分数阶互感，该电容器可以被忽略，因为如前所述，FMI 可以具有自补偿行为。因此，从电路实现的角度来看，使用分数阶互感进行匹配更简单，因而成本更低，因为它所需的元件更少。

由(17a)可知，负载阻抗除了与电路元件{$L_{11}$ , $L_{22}$ ,$M,Z_{in}$}有关外，还依赖于分数阶次 $\alpha$，从而提高了设计灵活性。输入阻抗对在 $\alpha$取较大值时，输出阻抗可以最小化，如图11(b)所示。因此，即使输入阻抗发生变化，系统仍可针对固定的负载阻抗进行设计。另一方面，当 $\alpha$取较小值时，输入阻抗对负载阻抗的影响非常大，如图11(b)所示。对于相同阶数（$\alpha=\beta=\gamma$）且$L_{11}= 1$mH、$L_{22}=M = 10\mu H$的情况，在图11(b)所示范围内，系统无需使用补偿电容即可保持稳定。因此，系统可在特定频率范围内实现匹配设计而无需使用补偿电容。通过改变分数阶的阶次以及电路元件值，可以调整该频率范围。

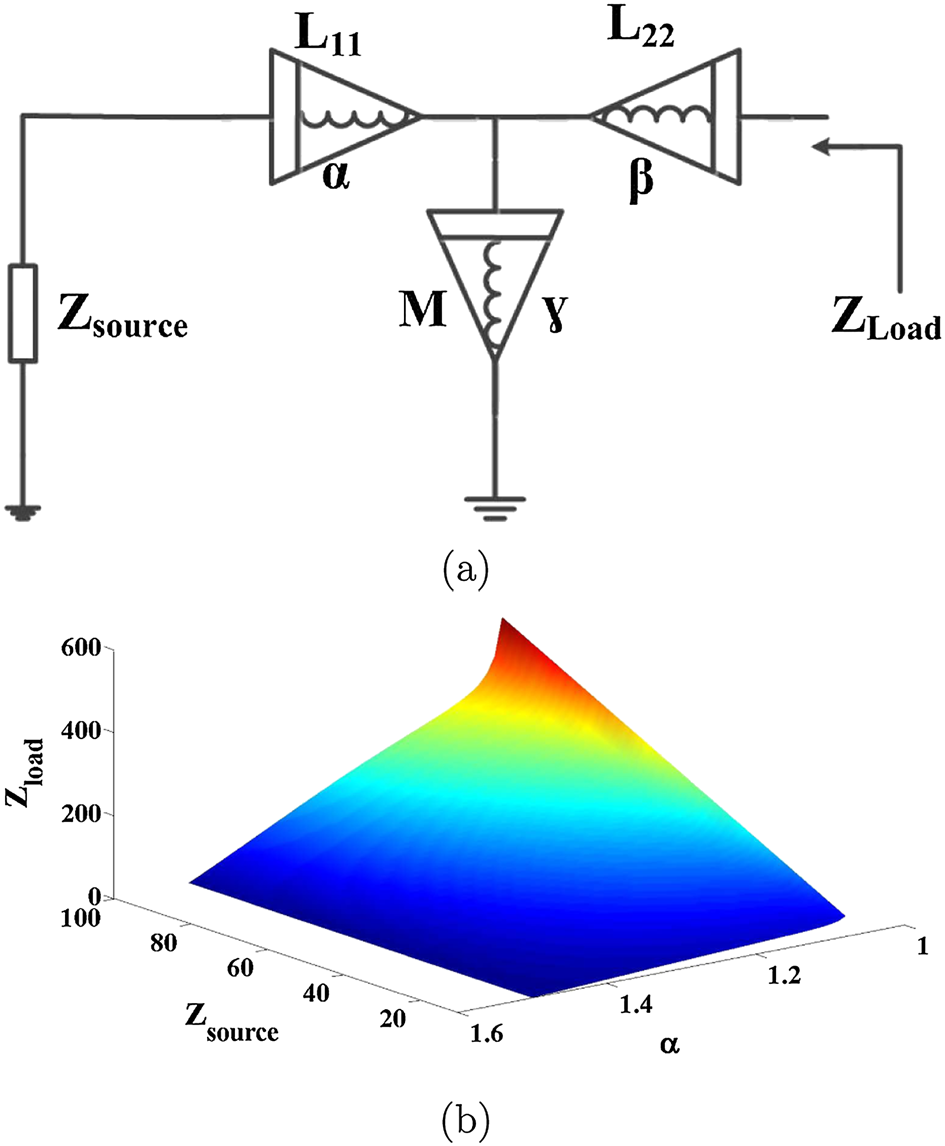使用分数阶互感耦合电路T型模型的阻抗匹配电路；(b) 在$L_{11}= 1$mH和$L_{22}=M= 10\mu H$条件下，关于 $Z_{Load}$、$Z_{source}$和 $\alpha$的数值分析)

5. 结论

讨论了分数阶互感分析。为了使用FMI，提出了一种等效电路。研究发现，如高级设计系统和MATLAB仿真所示，等效电路的阻抗矩阵参数的相位响应可以通过分数阶的取值进行控制。基于所提出的FMCC，讨论了不同的应用，如双调谐滤波器和阻抗匹配。对于双调谐滤波器，数值分析与高级设计系统仿真之间具有良好的匹配性。此外，针对基于所提出的FMCC的阻抗匹配，推导了设计方程，并且由于设计变量的增加，设计自由度也得到提高。