前言:
希尔排序(Shell Sort)是一种基于插入排序的排序算法,它的核心思想是通过将待排序元素按一定间隔分成若干组,并对每个组进行插入排序,进而达到加速排序的目的。
希尔排序开创性地突破了O(N²)时间复杂度瓶颈,成为计算机科学史上首个实现这一突破的排序算法。相较于传统的插入、选择和冒泡排序,它在性能上实现了质的飞跃。

一、传统插入排序的缺陷
为了更好地理解希尔排序的优势,我们首先回顾一下传统插入排序的工作原理。
插入排序的核心思想是将一个元素插入到已经排好序的部分,逐步构建整个排序。它的时间复杂度为O(N²) ,这是因为每插入一个元素,都需要和之前的元素逐一比较,最坏情况下每次插入都要进行n次比较和交换。
例如:假设我们需要对一个逆序数组[6,5,4,3,2,1]进行升序排序。在这种情况下,每个待插入元素都需要与已排序部分逐个比较和交换,导致性能下降,这是因为插入操作只能逐步向前移动。
那么,是否可以通过"跳式"多步的方式比较来优化插入排序呢? 希尔排序由此应运而生。
二、希尔排序的工作原理
希尔排序通过引入增量(gap)优化了插入排序,它通过逐步减小间隔(gap),将待排序数组划分成多个小的子序列,每个子序列通过插入排序来进行排序。
由于插入排序本身对已经部分有序的数组较为高效,希尔排序通过逐步缩小间隔,使得整个数组在多轮排序中逐步趋向有序,最终gap减小至1,执行插入排序使得整个数组有序。
其核心步骤如下所示:
①设定初始增量gap值,将数组元素按gap间隔分组
②对每个分组执行插入排序
③逐步减小gap值,重复分组排序过程
④当gap减至1时,执行标准插入排序完成最终排序
其中每次排序让数组接近有序的过程叫做预排序,最后一次排序是插入排序
以待排序数组 [8,9,1,7,2,3,5,4,6,0] 为例讲解希尔排序分组过程
1.以gap=3为增量,进行如下分组,如下所示待排序数组被分为三组
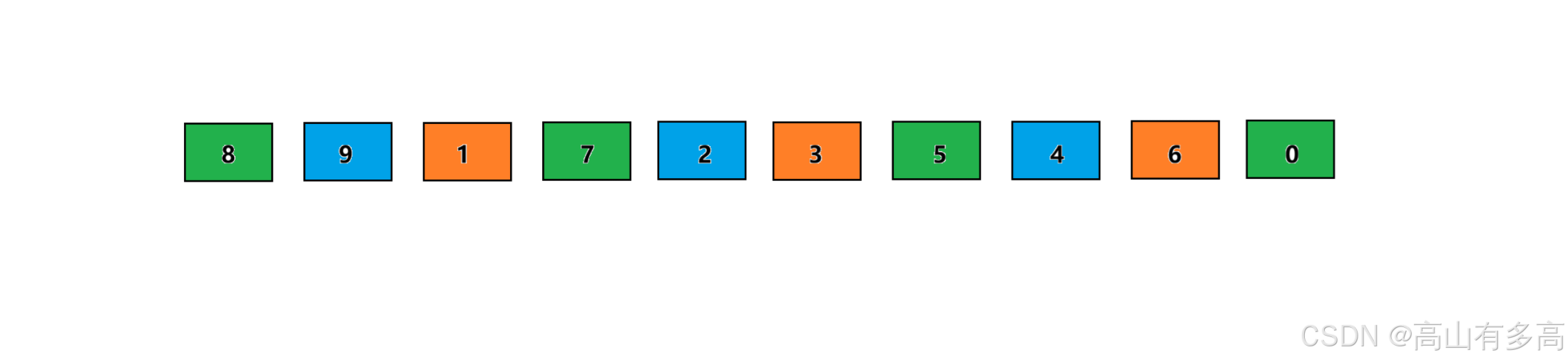
2.对每一组进行插入排序,则可得到如下数组
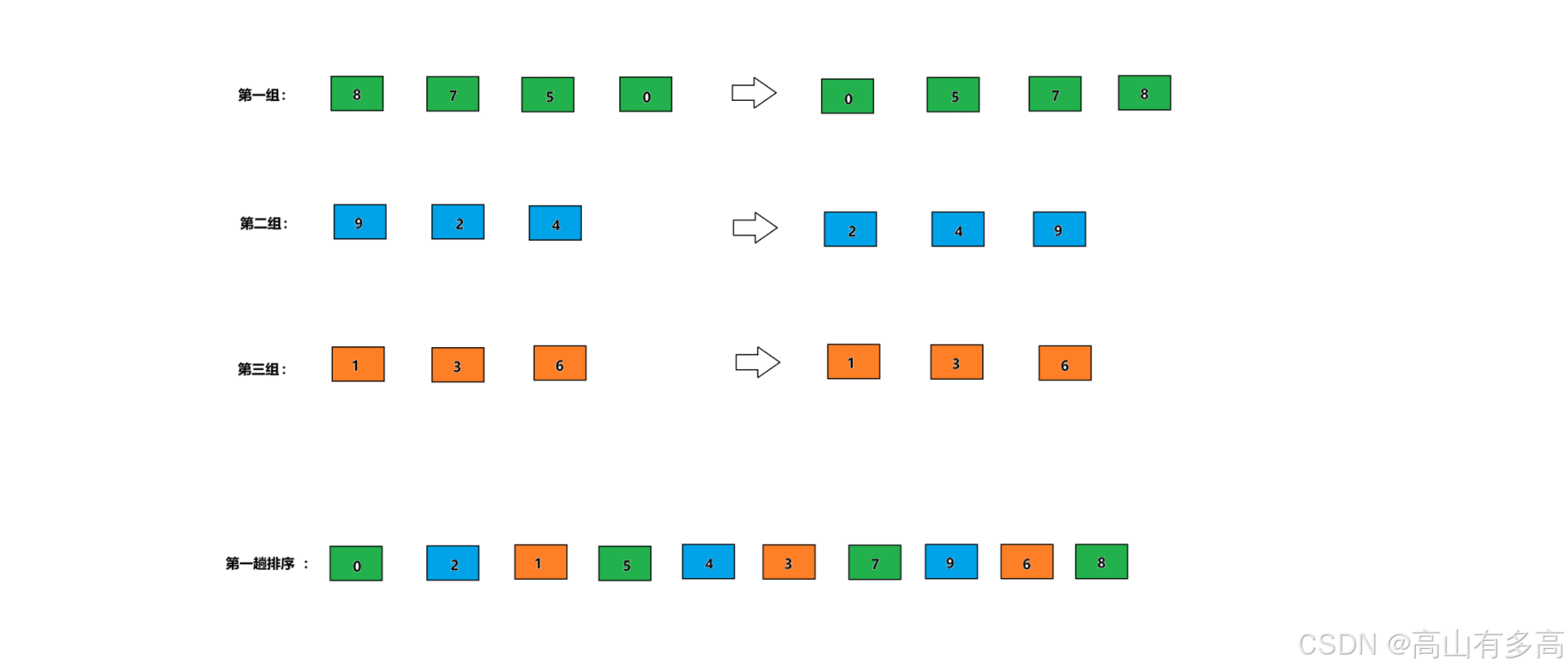
3.此时gap增量缩小,以gap=2为增量对数组进行分组,数组将被分成2份,每组之间都是2的等差数列
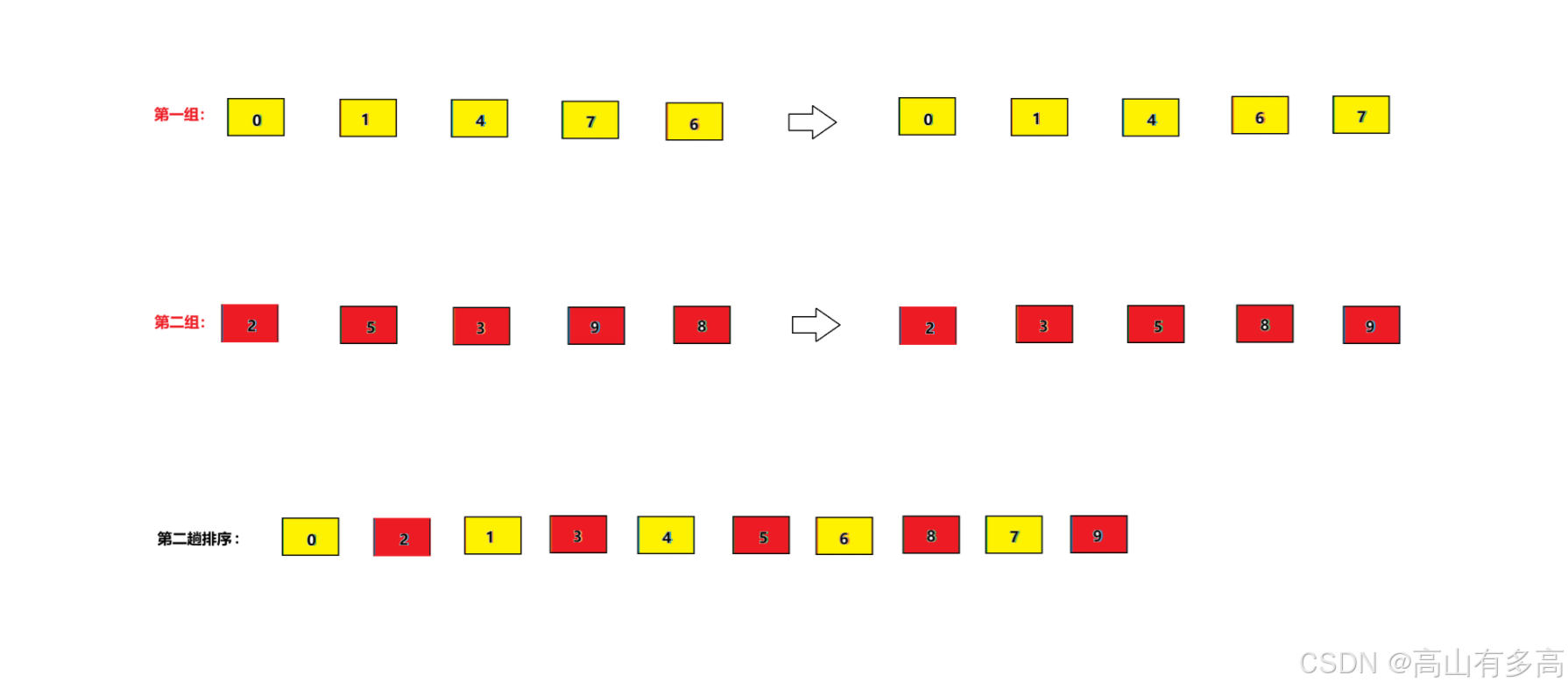
4.最后gap为1,以gap=1进行分组,相当于没有进行分组,就相当于进行插入排序

三、希尔排序的改进之处
对比第一次排序前后的结果可以发现,原本位于数组头部数值的较大元素,经过分组排序后迅速被移动到了数组尾部。
这种排序方式采用增量步长来腾出插入位置,相比普通插入排序一次移动一步的方式效率显著提升。
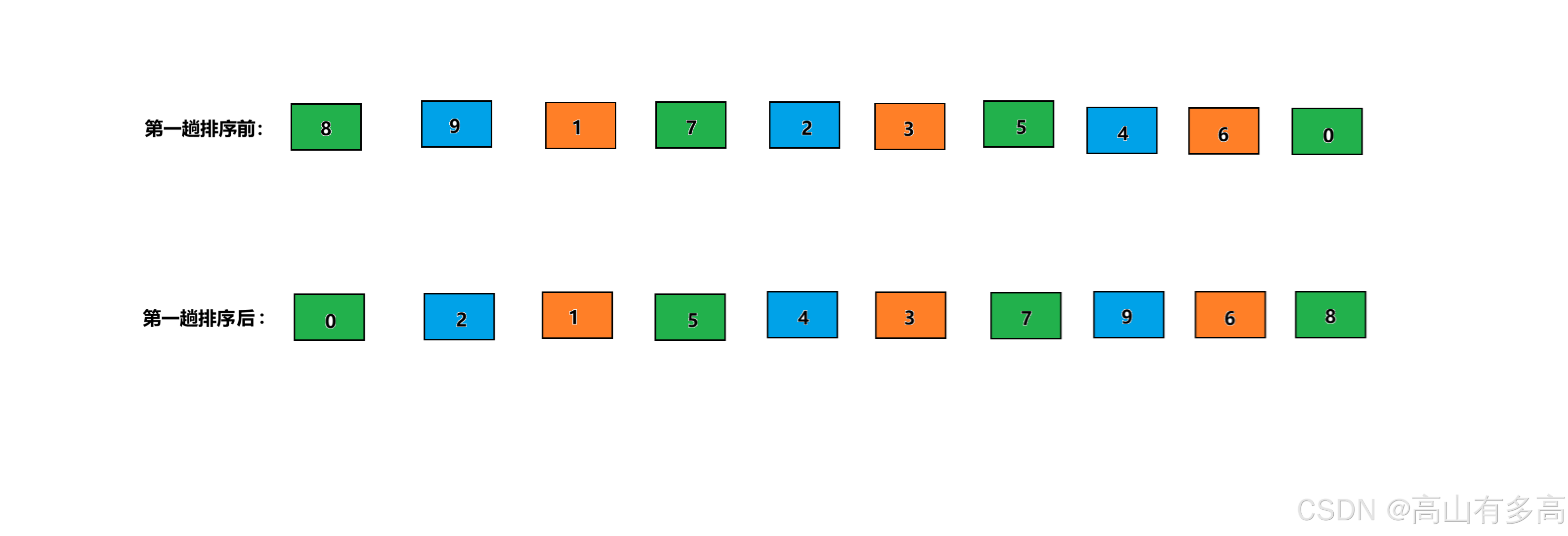
第一次排序后,我们采用更小的增量进行分组,经过第二趟排序以后,组与组之间更加有序
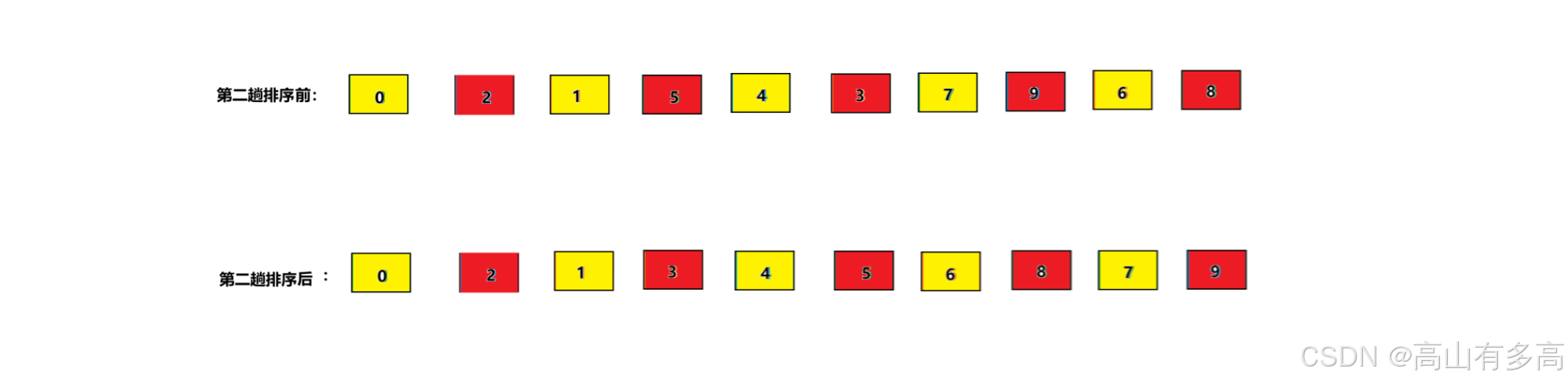
经过第二次排序后,我们采用gap=1的分组方式进行排序,这实际上等同于直接插入排序。
值得注意的是,此时的数组已接近有序状态。最初的无序数组直接执行插入排序操作与预排序之后再进行直接插入排序,所需的比较和移动次数将明显增多。
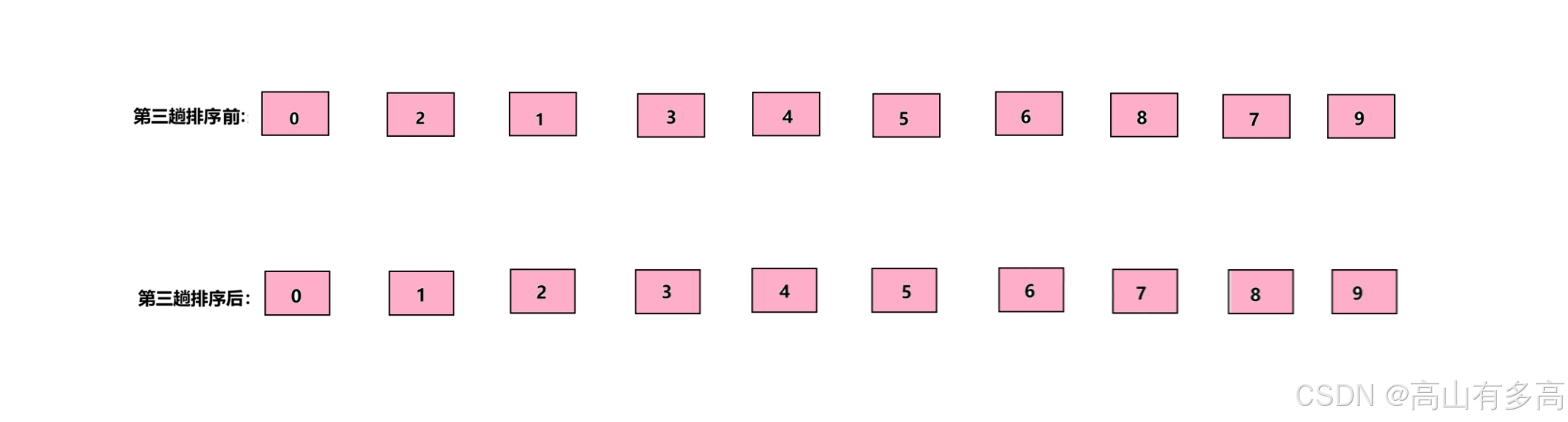
由上述,我们可以发现:
①当 gap 值越大时,数据会被分成更多组,组与组之间的有序程度越低;
②当 gap 值越小时,分组数量越少,组与组之间的有序程度越高;当 gap=1 时,该排序方式等价于插入排序。
③同时gap的值决定了分组的个数,因为每gap距离分为一组,所以gap的值为多少,待排数列就可以分为多少组。
例如:待排数列为 [8,9,1,7,2,3,5,4,6,0]
当
gap = 3时:
我们将数组按间隔
3分成多个组:
①组1:索引为 0, 3, 6, 9 的元素。
②组2:索引为 1, 4, 7 的元素。
③组3:索引为 2, 5, 8 的元素
四、希尔排序的分组策略
希尔排序中gap的选取没有 “绝对最优” 的统一规则,但有几种经典且常用的序列方案
核心原则是:初始 gap 要足够大以快速减少逆序对,后续逐步缩小,最终必须降到 1(保证数组完全有序)。
①希尔祖师爷提出的增量是
gap = n / 2
②Knuth大佬提出的gap = [gap / 3] + 1
五、希尔排序的代码实现
对于希尔排序代码实现的过程十分抽象难懂,由于我们讲解的希尔排序的思路是将待排序数组进行分组后,进行直接插入排序,这也就导致我们容易产生疑惑,是不是分多少组就调用多少次插入排序的代码呢?
实则不然,我们可以通过用一次遍历数组的方式,巧妙地对每个分组完成单趟排序,不需要对代码进行很复杂抽象的操作。
我们依然可以采用先局部再整体的方式进行对数组的排序: 假设gap的初始值为3,初始时对待排序数组进行分三组
如下图所示:以待排数组 [8,9,1,7,2,3,5,4,6,0] 为例进行代码的讲解

核心思路:对于第一组(绿色方块)的元素而言:进行插入排序的思路,通过将待排序的数组[ 7 , 5 , 0 ] ,插入到已经有序的数组 [ 8 ] 。
①定义变量end表示:有序数组中的最后一个元素下标
②定义tmp表示:待排序数组中,当前要插入到有序数组中的元素值,即tmp=a[end+gap]
例如:初始时已经有序的数组为[8],需要将a[end+gap]的值 7 插入到已经有序的数组中
③遍历第一组(绿色方块)的元素而言,每遍历一个元素需要跨越gap步的距离,而不是固定思维跨越一步的距离
④确定end的范围:为了使得待排序数组中的最后一个元素a[end+gap]也能插入到有序数组中,则end的最大值只能为n-gap-1,
故而确定得到end<gap-n
5.1、排序一组
由上述思路我们可以对绿色这一组进行排序
//数组:[8,9,1,7,2,3,5,4,6,0]
//下标:[0,1,2,3,4,5,6,7,8,9]
//进行升序排序
//假设gap=3
int gap = 3;
for (int i = 0; i < n - gap; i += gap)
{
//end下标为有序数组中的最后一个元素下标
int end = i;
//当前需要进行插入的元素
int tmp = a[end + gap];
//进行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往后移动
a[end + gap] = a[end];
//向前跨越gap进行遍历
end -= gap;
}
else
{
//找到合适的位置
break;
}
}
//退出while循环有两种情况
//情况一:当前插入的元素,在向前比较时,已排序数组中没有比其更小的,因不满足end>=0而退出
//情况二:当前插入的元素,在向前比较的时候找到了合适的位置,因break而退出
a[end + gap] = tmp;
}
通过该段代码,此时数组预期结果为:[0 9 1 5 2 3 7 4 6 8]

5.2、排序多组
有了排序绿色方块一组的基础,如果想要排序其他组,只需要在此基础上再添加一层循环,控制每组的起始位置就能够排序其余其他的组次
//数组:[8,9,1,7,2,3,5,4,6,0]
//下标:[0,1,2,3,4,5,6,7,8,9]
//进行升序排序
//假设gap=3
int gap = 3;
//控制每组的起始位置
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下标为有序数组中的最后一个元素下标
int end = i;
//当前需要进行插入的元素
int tmp = a[end + gap];
//进行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往后移动
a[end + gap] = a[end];
//向前跨越gap进行遍历
end -= gap;
}
else
{
//找到合适的位置
break;
}
}
//退出while循环有两种情况
//情况一:当前插入的元素,在向前比较时,已排序数组中没有比其更小的,因不满足end>=0而退出
//情况二:当前插入的元素,在向前比较的时候找到了合适的位置,因break而退出
a[end + gap] = tmp;
}
}
通过该段代码,此时数组预期结果为:[0 2 1 5 4 3 7 9 6 8]

5.3、缩小gap
我们通过缩小gap值的方式,数组从预排序变为几乎完全有序状态,最后当gap=1时,数组变为有序
//以数组:[8,9,1,7,2,3,5,4,6,0]
// 下标:[0,1,2,3,4,5,6,7,8,9]
//进行升序排序
//假设gap=3
int gap = 3;
//由于采用的是gap--的方式缩小gap,所以gap=1时也要进入
while (gap >= 1)
{
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下标为有序数组中的最后一个元素下标
int end = i;
//当前需要进行插入的元素
int tmp = a[end + gap];
//进行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往后移动
a[end + gap] = a[end];
//向前跨越gap进行遍历
end -= gap;
}
else
{
//找到合适的位置
break;
}
}
//退出while循环有两种情况
//情况一:当前插入的元素,在向前比较时,已排序数组中没有比其更小的,因不满足end>=0而退出
//情况二:当前插入的元素,在向前比较的时候找到了合适的位置,因break而退出
a[end + gap] = tmp;
}
gap--;
}
}
通过该段代码后,此时数组预期结果为:[0 1 2 3 4 5 6 7 8 9]

思考如下问题:
1.这仅仅是在gap=3的基础上实现,但每次分组只能为3吗?
2.每次缩小增量gap只能每次减小1吗?
答:当然不是,我们一般采用,Knuth大佬提出的gap = [gap / 3] + 1 或则 希尔祖师爷提出的增量 gap = n / 2 进行分组实现预排序
用上述增量的方式也能使得最后一次排序时gap=1,转变为直接插入排序。
5.4、完整实现
于是我们可以进行更改上述代码,采用这两种增量的方式调整gap,从而得到最终版本的希尔排序:
//以数组:[8,9,1,7,2,3,5,4,6,0]
// 下标:[0,1,2,3,4,5,6,7,8,9]
//进行升序排序
//假设gap=3
int gap = n;
while (gap > 1)
{
//shell增量 gap=gap/2
//knuth增量 gap=gap/3+1
gap = gap / 3 + 1;
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下标为有序数组中的最后一个元素下标
int end = i;
//当前需要进行插入的元素
int tmp = a[end + gap];
//进行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往后移动
a[end + gap] = a[end];
//向前跨越gap进行遍历
end -= gap;
}
else
{
//找到合适的位置
break;
}
}
//退出while循环有两种情况
//情况一:当前插入的元素,在向前比较时,已排序数组中没有比其更小的,因不满足end>=0而退出
//情况二:当前插入的元素,在向前比较的时候找到了合适的位置,因break而退出
a[end + gap] = tmp;
}
}
}
代码疑难点剖析:
int gap = n; while (gap > 1) { gap = gap / 3 + 1; //... }
想必对于这一部分逻辑会很疑惑,为什么这样控制gap呢?
之所以这样写,主要有两个原因:保证最后一次gap的值一定是 1,以及防止死循环。
1.while循环的条件
gap > 1: 保证了只要 gap 还没变到 1,就继续缩小,而且它把 gap = 2 放进来作为最后一次循环的临界条件,当gap=2时,配合gap的调整表达式使得gap=1,保证了最后一次循环进行的是插入排序。
2.gap处理的表达式
gap=gap / 3 + 1 : 每次 gap = gap / 3 + 1 计算,实际上是通过不断除以3和加1的方式逐渐减小gap的值,直到最后gap为1,加1有效的避免了因为整数除法被截断导致gap=0,而造成了死循环导致程序卡死。
这两段代码十分巧妙的结合在一起,感叹一下大佬们的智商
实例推演 (Trace) 🔍
让我们用一个具体的数字
gap = 8来跑一遍这个逻辑:
初始状态:gap = 8
第 1 次判断:8 > 1?👉 Yes。进入循环。
更新 gap:gap = 8 / 3 + 1 = 2 + 1 = 3。
执行排序:以 3 为增量进行排序。
第 2 次判断:3 > 1?👉 Yes。继续循环。
更新 gap:gap = 3 / 3 + 1 = 1 + 1 = 2。
执行排序:以 2 为增量进行排序。
第 3 次判断:2 > 1?👉 Yes。继续循环。
更新 gap:gap = 2 / 3 + 1 = 0 + 1 = 1。
执行排序:以 1 为增量进行排序。(注意:这里完成了最终的插入排序)
第 4 次判断:1 > 1?👉 No。
退出循环,排序结束。
六、希尔排序代码的总结
6.1写法一(方便理解的写法)
通过gap进行分组后,一组一组排序
void ShellSort(int* a, int n)
{
//以数组:[8,9,1,7,2,3,5,4,6,0]
// 下标:[0,1,2,3,4,5,6,7,8,9]
//进行升序排序
//假设gap=3
int gap = n;
while (gap > 1)
{
//shell增量 gap=gap/2
//knuth增量 gap=gap/3+1
gap = gap / 3 + 1;
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下标为有序数组中的最后一个元素下标
int end = i;
//当前需要进行插入的元素
int tmp = a[end + gap];
//进行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往后移动
a[end + gap] = a[end];
//向前跨越gap进行遍历
end -= gap;
}
else
{
//找到合适的位置
break;
}
}
//退出while循环有两种情况
//情况一:当前插入的元素,在向前比较时,已排序数组中没有比其更小的,因不满足end>=0而退出
//情况二:当前插入的元素,在向前比较的时候找到了合适的位置,因break而退出
a[end + gap] = tmp;
}
}
}
}
6.2写法二(主流书上的写法)
通过gap进行分组后,组与组之间交替的进行排序
这是在写法一的基础上进行改进减少代码量,但是在性能上与写法一没有本质区别,只是逻辑发生了改变,写法一是一组一组排,当一组排序完毕后,另一组才开始继续排需要多一层循环控制组数的起点
以下图为例,对于写法二而言,这是组与组之间交替着排序,当绿色一组排序完一个,轮替到蓝色一组排序一个,再轮替到橙色一组排序一个,这也交替着进行,多组并行的方式进行调整各自组的有序性。
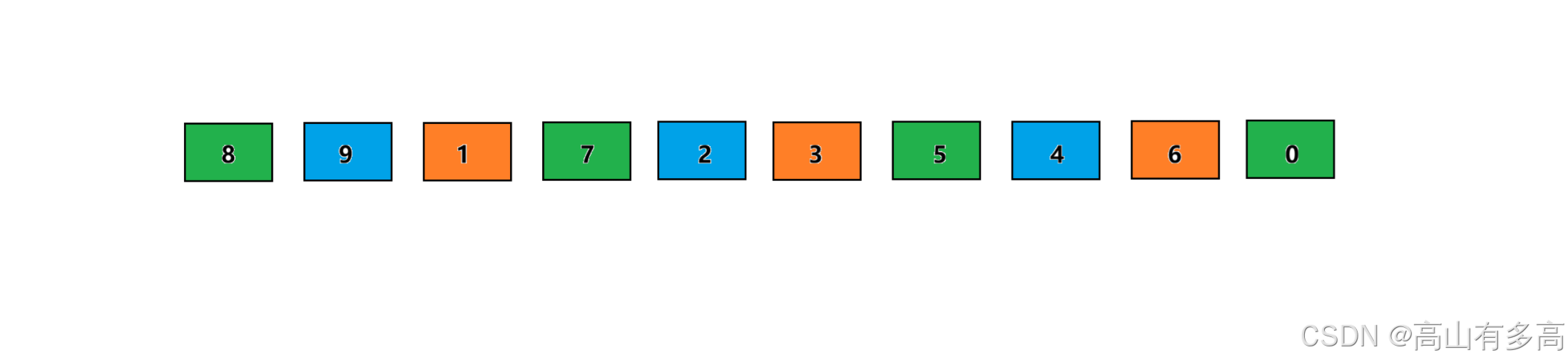
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//预排序
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
七、希尔排序复杂度分析
时间复杂度分析
对于希尔排序的时间复杂度没有明确的数学表达式进行定量分析,但是经过大量数据验证认定:
| 增量序列类型 | 最坏时间复杂度 | 平均时间复杂度 | 适用场景 |
|---|---|---|---|
| 二分增量(传统) | O(n²) | O(n²) | 教学演示,无需追求效率的场景 |
| Hibbard 序列 | O(n^(1.5)) | O(n^(1.3)) | 平衡效率与实现复杂度,推荐首选 |
| Sedgewick 序列 | O(n log²n) | 接近 O (n log n) | 大规模数据,追求极致效率 |
空间复杂度分析
希尔排序的空间复杂度为 O(1),属于 “原地排序” 算法。
既然看到这里了,不妨关注+点赞+收藏,感谢大家,若有问题请指正。























 997
997










