基于五项系统的多翼混沌吸引子

基于五项三维系统的多翼混沌吸引子的设计与实现

1. 引言

自从洛伦兹发现第一个洛伦兹混沌吸引子以来[1], ，许多科学家和工程师更加关注线性或非 线性系统中混沌特性的研究[2–5]。由于混沌系统中表现出非周期振荡，因此在天气预报领域 存在许多混沌现象。此外，混沌已应用于化学、物理、空间技术、计算机技术、经济运行预 测、微生物学、伦理学、计量学等众多其他领域[6]。

众所周知，混沌吸引子可以从包含五个以上项的常微分方程中产生。1994年，斯普罗特 首次提出仅包含五项的混沌系统：_x ¼ y；_y ¼ yz x；_z ¼ x2 þ 1。随后，斯普罗特 提出了最简单的耗散混沌系统[8],，蒙芒森则给出了一个仅含五项的简单三阶常微分方程[9]。

之后，通差伦等人[10]提出了一种不同的、同样仅含五项的混沌吸引子，其表达式为_x ¼ 2 yz；_y ¼ x y；_z ¼ y2 þ 3:8，并且他们在实验中发现波形与常见的心形信号相似。迄 今为止，任何少于五项的传统常微分方程都无法生成混沌吸引子。

此外，多卷混沌系统的设计与电路实现已引起广泛关注，并提出了多种多翼混沌电路。例如，著名的双翼蔡氏电路由蔡少棠提出[11]。另一类多翼混沌吸引子，即具有n‐双吸引子的混沌吸引子，由苏延斯和范德瓦勒提出[12]。此外， 各种具有严格证明和物理实现的多涡卷混沌吸引子也已被研究[13–20]。进一步地，在过去 二十年中，我们观察到多涡卷混沌吸引子在工程领域的有意义应用[16, 17]。

最近，许多不同材料的数学模型可以用分数阶形式[21, 22],表示，许多其他电子问题也 可以用分数阶形式[23]描述。蔡氏系统、陈系统和吕系统的分数阶形式可以表现出混沌[24– 26]。但是，传统的整数阶系统与分数阶形式之间存在许多本质差异，且在整数阶系统中观察 到的许多特征或获得的结果不能简单地推广到相应的分数阶形式。

此外，混沌的许多其他应用也已被研究。在[27],中提出了一种控制器，以实现永磁同 步电机系统的有限时间混沌抑制。我们可以基于有限时间稳定性理论来分析永磁同步电机的 混沌抑制。罗布莱多[28]已完成关于动态状态如何在许多复杂系统（如光谱、层序和复杂网 络图像）中转变为混沌的报告。其他研究也探讨了混沌系统在复杂网络领域所起的作用[29– 31]。

本文中，首先，通过分段线性函数[32]在五项三阶常微分方程中获得了若干不同于以往 研究的多翼蝴蝶混沌吸引子。其次，我们关注该新系统的若干动力学特性，包括对称性、耗 散性、平衡点、雅可比矩阵的特征值、李雅普诺夫指数谱、分岔图和庞加莱映射。第三，我 们在该新系统中得到了分数阶多涡卷混沌吸引子。此外，还设计了相应的改进的模块化电路， 通过试错法实现了前述混沌吸引子。

本文的结构如下：在第2节中，介绍了本文采用的五项简单混沌吸引子，并展示了使用 MATLAB进行的一些相应数值仿真。在第3节中，通过引入一个分段线性函数，使五项系统 产生了多涡卷蝴蝶混沌吸引子。在第4节中，揭示了该系统的一些相关特性。多翼混沌电路在 第5节中建立。0.1阶多翼混沌系统也在第6节中构造完成。所有吸引子均在示波器上观察到。 最后，我们给出了结论。

2. 五项简单混沌吸引子

根据洛伦兹系统中的混沌理论，通过对洛伦兹混沌方程增加或减少一项，可以得到多种变换。 此处，我们在第二个微分方程中增加一项，例如l1= rx+y，并在洛伦兹系统的第三个微分 方程中增加一项，如l2= bz a2。因此，可得到一个仅包含五项的新三阶系统，并可写为[9]

$$
\begin{cases}
\dot{x} = a_1(-x + y) \
\dot{y} = -xz \
\dot{z} = xy - a_2
\end{cases}
\quad (1)
$$

系统（1）包含两个非线性项、两个线性项和一个常数项。当a1 =5、a2 =80及初始条件 {x(0),y(0),z(0)}={5,10,5}时，系统（1）可生成混沌吸引子，如图1(a)–(c)所示。显然，系 统（1）能够表现出丰富的混沌行为，且图1中的混沌吸引子在形状上呈现出类似蝴蝶的特征， 这与我们此前发现的结果不同。

3. 一种基于分段线性函数的新多翼混沌吸引子

此前，许多基于洛伦兹型系统[19,33]的超混沌吸引子和多翼吸引子被提出。如果我们在一个 参数可调的二次系统中增加或替换一项，则可以生成多翼吸引子[19],，并且该混沌系统的 平衡点数量从2个变为2Q个+ 2。陈等人[13]提出了一种新的多涡卷混沌系统，可用于描述多 涡卷混沌系统的不同方面。张和余[14]以吕系统为典型例子，进一步研究了生成复杂网格多 翼四维超混沌系统的其他一些新方法。此外，在[20]中还提出了一种生成多种多涡卷混沌吸 引子的新途径。在此，将一种新的分段线性函数应用于五项系统中，以产生双翼蝴蝶混沌吸 引子，具体如下所示

$$
f(x) = x + 2(P + 1) - 2 \sum_{n=-Q}^{P} \varepsilon(x + 2n + 1)
\quad (2)
$$

其中P,Q ∈{0,1,2,…}。

ε(x+ 2n+ 1)是一个单位阶跃函数，该单位阶跃函数的示意图如图2所示。

在将f(x)用于替换系统（1）中的状态变量x，并适当修改系统参数后，可以得到一个新系统：

$$
\begin{cases}
\dot{x} = a_1[-f(x) + y] \
\dot{y} = -d_1 z f(x) \
\dot{z} = d_2 f(x)y - (1/d_2)a_2
\end{cases}
\quad (3)
$$

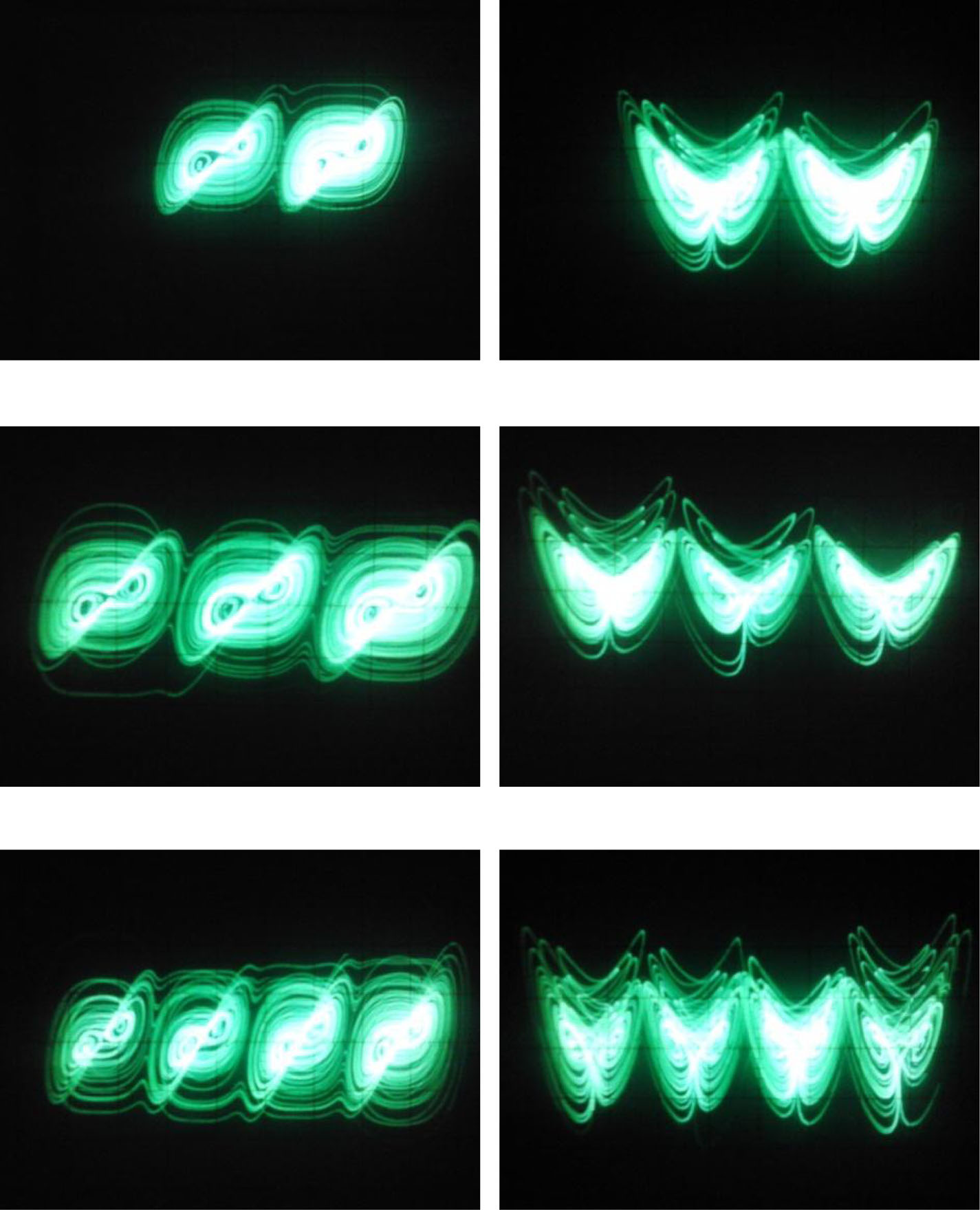
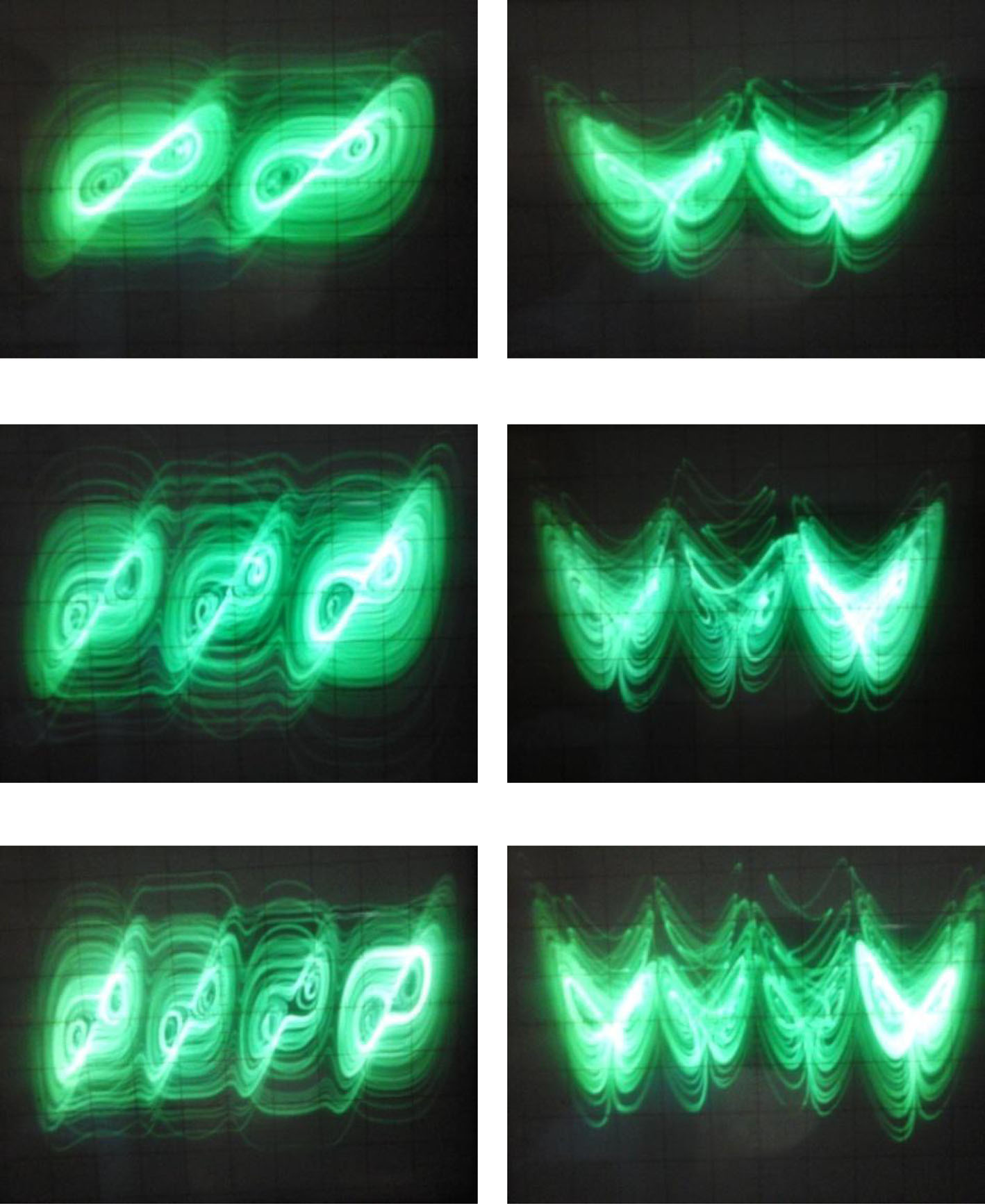
参数固定为a1= 5，a2= 80，d1= d2= 20，可得到2(P+ Q+ 1)‐翼混沌蝴蝶吸引子。考虑 到吸引子的范围足够大，我们缩小了图3中相图的比例。当P= Q= 0时，在xy平面和x z 平面上分别得到了四翼混沌吸引子，如图4(a)和(b)所示。当P= 1，Q= 0时，在xy平面和 x z平面上分别得到了六翼混沌吸引子，如图4(c)和(d)所示。当P=Q=1时，在xy平面 和x z平面上分别得到了八翼混沌吸引子，如图4(e)和(f)所示。

x‐y平面；(b)x‐z平面；和(c)y‐z平面。)

4. 新多翼混沌系统的一些简单性质

4.1. 对称性与耗散性

当f(x)=x时，系统(3)关于z轴对称，并且在以下变换下保持不变：

$$
(x, y, z) \Rightarrow (-x, -y, z)
\quad (4)
$$

然后，该混沌系统(3)的散度为

$$
\nabla V = \frac{\partial \dot{x}}{\partial x} + \frac{\partial \dot{y}}{\partial y} + \frac{\partial \dot{z}}{\partial z} = -a_1
\quad (5)
$$

当a1 > 0时，系统(3)具有耗散性，其体积可收敛至

$$
\frac{dV}{dt} = e^{-a_1 t}
\quad (6)
$$

换句话说，对于该体积V 0 , Vtð Þ ¼ V0e a 1 t。因此，系统（3）中产生了一个吸引子).

4.2. 平衡点与雅可比矩阵的特征值

平衡点可以通过求解以下方程得到：

$$
\begin{cases}
a_1[y - f(x)] = 0 \
-d_1 f(x)z = 0 \
-a_2(1/d_2) + d_2 f(x)y = 0
\end{cases}
\quad (7)
$$

显然，存在两个非零平衡点：

$$
S_1 = \left( \sqrt{\frac{a_2}{d_2}} + 2m, \sqrt{\frac{a_2}{d_2}}, 0 \right),
S_2 = \left( -\sqrt{\frac{a_2}{d_2}} + 2m, -\sqrt{\frac{a_2}{d_2}}, 0 \right)
\quad (8)
$$

其中m={P,,1, 0, 1,,Q}。

在平衡点S*=(x*,y*,z*)处对系统(3)进行线性化，得到雅可比矩阵为

$$
J =
\begin{bmatrix}
-a_1 g(x^ ) & a_1 & 0 \
-d_1 g(x^ ) z^ & 0 & -d_1 f(x^ ) \
d_2 g(x^ ) y^ & d_2 f(x^*) & 0
\end{bmatrix}
\quad (9)
$$

这里，S*=(x*,y*,z*)表示平衡点S1 或S2的坐标。

$$
g(x^ ) = \left. \frac{df(x)}{dx} \right|_{x=x^ } = 1 - 2 \sum_{n=-Q}^{P} \delta(x^* + 2n + 1)
\quad (10)
$$

其中 δ()是脉冲函数，x* ≠(2n+ 1)，且 δ(x*+ 2n+ 1)= 0；因此，

$$
g(x^*) = 1
\quad (11)
$$

如果我们将S1 ¼ ffiffiffiffiffia p2= 0 2 þ 2 p2= 2 dm;ffiffiffiffiffiad;代入 方程det(JλI)= 0，并在参数a1= 5,a2= 80,d2= 20下计算其特征值，则得到的三个特征 值分别为λ1= 7.41, λ2,3= 1.2 ± 10.32i，因为 λ1 是一个负实数，而 λ2 和 λ3是具有正实 部的共轭复特征根。因此，平衡点S1 是一个不稳定的鞍焦型点，所以系统(3)在S1处是不稳 定的。类似地，我们可以求得在平衡点S2, 的另外三个特征值，其形式与平衡点S1处的特征 值相似。此外， λ1 是一个负实数，而 λ2和 λ3 是一对具有正实部的共轭复特征根。因此， 平衡点S2 也是一个鞍焦型点，所以系统(3)在S2处也是不稳定的。于是，该系统的两个平 衡点均为鞍焦型节点。

4.3. 李雅普诺夫指数谱和分岔图

尽管迄今为止尚未发现生成混沌的完整理论，但在研究混沌系统中的动力学行为方面仍有一 些有效的方法，其中最著名的是李雅普诺夫指数谱和分岔图。对于一个三维自治系统，存在 一个正值、一个零值和一个负值的李雅普诺夫指数。

在系统(3)中，固定a1= 5、a2= 80、d2= 20和P= Q= 0的取值，参数d1变化对李雅普诺夫 指数谱的影响如图5所示，相应的分岔图如图6所示。结果表明，所获得的分岔图与李雅普诺 夫指数谱具有一致性。系统(3)中随着d1的增加所产生的动力学行为总结如下。

当d1 ∈[0, 0.9] ∪[1.52，1.9],时，图5中所示的最大李雅普诺夫指数等于零，表明系统 (3)具有周期轨道。当d1 ∈[1.9，15.3] ∪[15.8, 20],时，第一李雅普诺夫指数（LE）为正，第 二LE为零，第三LE为负，这一现象表明混沌存在。随着d1进一步增大，系统进入稳定的混 沌区域；分岔图也支持这一结论。该系统中的最大李雅普诺夫指数可达1.53。

在较大区域内是一个混沌系统；第一李雅普诺夫指数用蓝色标记，第二李雅普诺夫指数用绿色标记，第三李雅普诺夫指数用红色标记。)

中变量x关于参数d1的分岔图。所有点均在舍弃前100个点后获得，该图清晰地展示了通向混沌的周期路径。)

4.4. 庞加莱映射

庞加莱映射通常反映一个系统中的分岔和折叠曲面。当系统(3)的参数取为a1= 5、a2= 80、 d1= d2= 20、P= Q= 0时，系统(3)的庞加莱映射如图7所示。该结果与前一节中所示的李雅 普诺夫指数谱和分岔图高度一致。

的庞加莱映射。(a) 在y‐z平面上的投影和(b) 在x‐y平面上的投影。该映射中获得的所有数据点均反映了四翼蝴蝶混沌吸引子的相图。)

5. 新型多翼混沌系统的电路实现

在本部分中，已在Multisim中构建了一个模块化程序，以实现多翼混沌吸引子，如图8所示。 在该电路中，我们使用了电源为 ±15V的LF347N运算放大器，其输出饱和值为V sat ≈135V； 使用的乘法器为AD633JN，其增益为0.1。正负极分别连接VCC和VEE。R30是一个100kΩ 的电位器。系统(3)中的归一化电阻也为100kΩ。

根据系统(3)，电路方程描述为

$$
\begin{cases}
\frac{dx}{d\tau} = \frac{1}{R_8 C_1} \left( \frac{R_7}{R_1} y - \frac{R_7}{R_2} f(x) \right) \
\frac{dy}{d\tau} = \frac{1}{R_{10} C_2} \left( -\frac{R_9}{10 R_4} f(x) z \right) \
\frac{dz}{d\tau} = \frac{1}{R_{12} C_3} \left( \frac{R_{11}}{10 R_5} f(x) y + \frac{R_{11}}{10 R_6} V_1 \right)
\end{cases}
\quad (12)
$$

为了观察实验的输出波形， τ需要在时间尺度上进行变换，即τ=τ₀t；令 τ₀= 10⁻³。 方程被变换如下：

$$
\begin{cases}
\frac{dx}{d\tau} = \frac{10^{-3}}{R_8 C_1} \left( \frac{R_7}{R_1} y - \frac{R_7}{R_2} f(x) \right) \
\frac{dy}{d\tau} = \frac{10^{-3}}{R_{10} C_2} \left( -\frac{R_9}{10 R_4} f(x) z \right) \
\frac{dz}{d\tau} = \frac{10^{-3}}{R_{12} C_3} \left( \frac{R_{11}}{10 R_5} f(x) y + \frac{R_{11}}{10 R_6} V_1 \right)
\end{cases}
\quad (13)
$$

所有电容均设为1纳法，根据公式(3)和(13)，在图8(b)中设置R₁ = R₂ = 20kΩ、R₄ = R₅ = 300 Ω、R₆ = 100kΩ、 R₃₈ = 12kΩ、R₃₉ = 14kΩ、R₁₅ = R₁₉ = R₂₃ = 13.5kΩ以及R₁₆ = R₂₀ = R₂₄ = 1.0kΩ；同时设置R₄₀ = R₄₁ = R₄₂ = R₄₃ = 1.0kΩ；此外，其他电阻均为10kΩ。

我们得到

$$
V_{k1} = -V_{\text{sat}} \frac{R_{24}}{R_{23}} \text{sgn}(x - 3R_{24}/R_{38}) + 3R_{24} V_{EE} - \frac{R_{24}}{R_{24} + R_{39}} V_{CC} = -2\varepsilon(x + 3)
\quad (14)
$$

此外，

$$
V_k = -V_{\text{sat}} \frac{R_{20}}{R_{19}} \text{sgn}(x - R_{20}/R_{38}) + 3R_{20} V_{EE} - \frac{R_{20}}{R_{20} + R_{39}} V_{CC} = -2\varepsilon(x + 1)
\quad (15)
$$

$$
V_{k2} = -V_{\text{sat}} \frac{R_{16}}{R_{15}} \text{sgn}(x - R_{16}/R_{39}) - \frac{R_{16}}{R_{16} + R_{39}} V_{CC} = -2\varepsilon(x - 1)
\quad (16)
$$

其中，
$$
\text{sgn}(z) =
\begin{cases}
1, & z > 0 \
0, & z = 0 \
-1, & z < 0
\end{cases}
$$

因此，当P= Q= 0时，k闭合且k₁ 和k₂ 断开。设置R₃₀= 75 kΩ；我们得到

$$
f(x) = x + V_k + \frac{R_{32} V_{CC}}{R_{30}} = x + 2 - 2\varepsilon(x + 1)
\quad (17)
$$

然后，得到了一个四翼混沌吸引子，如图9(a)和(b)所示。当P= 1、Q= 0时，k和k₁均 连接；k₂断开。设置R₃₀= 37.5kΩ；我们得到

$$
f(x) = x + V_k + V_{k1} + \frac{R_{32} V_{CC}}{R_{30}} = x + 4 - 2\varepsilon(x + 1) - 2\varepsilon(x + 3)
\quad (18)
$$

然后，得到了一个六翼混沌吸引子，并在图9(c)和(d)中展示。当P= Q= 1时，所有 的k,k₁, k₂均被连接；设置R₃₀= 37.5kΩ，我们得到

$$
f(x) = x + V_k + V_{k1} + V_{k2} + \frac{R_{32} V_{CC}}{R_{30}} = x + 4 - 2\varepsilon(x - 1) - 2\varepsilon(x + 1) - 2\varepsilon(x + 3)
\quad (19)
$$

然后，八翼混沌吸引子显示在图9(e)和(f)中。实验结果与数值仿真结果保持一致。

系统(3)的电路和(b) 分段线性函数f(x)的电路。)

在示波器上观察到的多翼蝴蝶吸引子轨迹。(a) 在x‐y平面获得的四翼吸引子；(b) 在 x‐z平面获得的四翼吸引子；(c) 在x‐y平面获得的六翼吸引子；(d) 在x‐z平面获得的六翼吸引子； (e) 在x‐y平面获得的八翼吸引子；以及(f) 在x‐z平面获得的八翼吸引子。)

6. 分数阶多翼混沌系统

分数阶微积分理论中有许多定义，本文所采用的定义是积分与微分的结合，其中积分微分算 子Dα t 是一个描述为非整数阶的算子。

$$
{} {a}D^{\alpha} {t} =
\begin{cases}
\frac{d^\alpha}{dt^\alpha}, & \Re(\alpha) > 0 \
1, & \Re(\alpha) = 0 \
\int_{a}^{t} (d\tau)^{-\alpha}, & \Re(\alpha) < 0
\end{cases}
\quad (20)
$$

在各种分数阶定义中，最常用的是由[21],指定的黎曼‐刘维尔（R‐L）定义

$$
D^\alpha x(t) = \frac{d^n}{dt^n} J^{n-\alpha} x(t); \quad \alpha > 0;
\quad (21)
$$

其中n=[α]，例如，n是不小于 α的最小整数；Jβ 是一个 β阶R–L积分算子，其定义如下

$$
J^\beta \phi(t) = \frac{1}{\Gamma(\beta)} \int_{0}^{t} \frac{\phi(\tau)}{(t - \tau)^{1-\beta}} d\tau
\quad (22)
$$

其中 Γ()是伽马函数，当且仅当 0<β ≤1。

根据公式(1)，该分数阶系统表示为

$$
\begin{cases}
\frac{d^\alpha x}{dt^\alpha} = a_1(-x + y) \
\frac{d^\alpha y}{dt^\alpha} = -xz \
\frac{d^\alpha z}{dt^\alpha} = xy - a_2
\end{cases}
\quad (23)
$$

其中 α是满足 0<α ≤1的分数阶。

在实际计算中，有许多方法可用于求解该运算，这些方法由分数阶微积分实现。其中两 种最常用的方法如下：一种是时域变换，另一种是复频域变换。为了获得复频域

通过求解复频域传递函数1/sq进行频域展开，我们将复频域转换到时域以进行数值计算。 Ahmad和斯普罗特[34]给出了0.1到0.9阶1/sq的展开方程。其中，0.1阶的展开方程具有最 大偏差2dB。

为简洁起见，如图10所示，A和B之间等效电路的复频域表达式为

$$
G(s) = \frac{1}{C_1 s + 1/R_1 C_1} + \frac{1}{C_2 s + 1/R_2 C_2} + \cdots + \frac{1}{C_n s + 1/R_n C_n}
\quad (24)
$$

当参数固定为n= 3，q= 0.1时，1/s⁰·¹ 的单元电路可在图11中实现，且A和B之间的传递函数为

$$
G(s) = \frac{1}{C_1 s + 1/R_1 C_1} + \frac{1}{C_2 s + 1/R_2 C_2} + \frac{1}{C_3 s + 1/R_3 C_3}
\quad (25)
$$

C₀是一个单位参数，其值为C₀= 1μF，因此

$$
G(s) = W(s)/C_0
\quad (26)
$$

对于W(s)= 1/s⁰·¹，比较公式(25)和公式(27)：

$$
\frac{1}{s^{0.1}} \approx \frac{1584.893 (s + 0.167)(s + 27.8)}{(s + 0.1)(s + 16.7)(s + 278)}
\quad (27)
$$

图11中该分数阶电路的参数设置为C₁= 15.72 μF、C₂=0.157 μF和C₃=633.5pF，以及R₁= 0.636MΩ、R₂=0.382MΩ和R₃=0.567MΩ。随后，我们获得了单元电路中的元件参数值， 该电路能够基于分数阶单元结构产生混沌振荡现象。

该新系统可以获得分数阶形式。如果仅将参数选择为a₁= 5、a₂= 80，且初始条件为 {x(0),y(0),z(0)}={5,10,5}。我们的电路实验结果验证了当该分数阶系统的阶数低至0.1时 仍可存在混沌。随后，分数阶系统(23)呈现出如图12所示的混沌行为。此外，当 α= 0.1时， 在适当参数下发现了多翼蝴蝶混沌吸引子，如图13所示。

的混沌吸引子；分数阶为0.1。（a）x–y平面中的吸引子；（b）x‐z平面中的吸引子；（c） y‐z平面中的吸引子。)

的多翼蝴蝶混沌吸引子；分数阶为0.1。(a) x‐y平面上的四翼蝴蝶混沌吸引子；(b) x‐z平面上的四翼蝴蝶混沌吸引子；(c) x‐y平面上的六翼蝴蝶混沌吸引子；(d) x‐z平面上的六翼蝴蝶混沌吸引子；(e) x‐y平面上的八翼蝴蝶混沌吸引子；(f) x‐z平面上的八翼蝴蝶混沌吸引子。)

7. 结论

在本研究中，我们提出了一种基于五项三维系统并利用分段线性函数生成多涡卷混沌吸引子 的新方法。同时，研究了一些基本特性，如对称性、耗散性、平衡点、雅可比矩阵的特征值、 李雅普诺夫指数谱、相应的分岔图以及庞加莱映射。此外，我们还提供了一些计算机仿真结 果，以验证多翼吸引子的存在，从而展示其复杂性和丰富的动力学行为。进一步地，当系统 的阶数降低至0.1时，我们在其对应的分数阶形式中也观察到了多翼吸引子。未来的工作可能 会聚焦于该多涡卷系统的大量动力学特性，以有意义地扩展当前的研究。