基于单片机的五维超混沌安全通信

基于新型五维超混沌系统的单片机安全通信

摘要

本文提出了一种基于单片机的用于安全通信的五维超混沌系统。首先，构建了一个五维超混沌系统，并对其平衡稳定性与李雅普诺夫指数等特性进行了分析。研究了该系统在不同参数下的状态，包括周期性、超混沌和混沌状态。接着，对系统的复杂度进行了分析，通过分析各维度的复杂度，验证了系统选择的正确性，并选取复杂度最高的维度用于通信加密。然后设计了硬件电路，通过仿真完成了方波信号的加密与解密，实现了安全通信。最后，调整了系统精度以及实现单片机混沌的算法，经0‐1检验验证，调整后的系统处于混沌状态，成功利用单片机生成了混沌。采用单片机可大幅降低信号加密的硬件成本，而将五维超混沌系统应用于安全通信，不仅能提高安全性，还能增强信号传输过程中的抗干扰能力。

关键词 安全通信 · 五维超混沌系统 · 单片机 · 仿真

1 引言

随着信息科学与通信技术的快速发展，基于计算机和互联网的信息网络正在形成并不断完善。科学技术以及社会、军事、金融等领域的进步与发展都离不开信息通信的安全。在当今社会，安全准确的信息已成为组织之间甚至国家之间交流的重要手段。确保各类信息传输与处理的安全至关重要。当数据量加密数据量大时，加解密效率低下的缺点逐渐显现。传统信息加密技术的安全性已无法完全满足安全技术的需求。此时，我们需要寻找一种新的加密算法来确保通信系统的安全。

混沌科学是二十世纪后期形成的一门综合性科学分支，继相对论和量子力学之后，成为又一次具有革命性和重大意义的科学进步。由于混沌系统产生的混沌信号具有类随机、连续宽带谱和类噪声特性，因此适用于信息加密和安全通信[1–3]。近年来，混沌理论受到广泛关注和研究，在混沌安全通信应用方面取得了丰硕成果[4–11]。

混沌安全通信[12], 混沌调制通信[13], 混沌掩盖通信[14]等。混沌掩盖通信的原理是在发送端将要传输的信息隐藏到混沌系统产生的混沌信号中，在接收端通过混沌同步去除接收到信号中的混沌信号，从而恢复原始信息。混沌移位键控通信的原理是在发送端使用两个不同的混沌信号分别表示0和1。接收器由两个与发射器相同的混沌振荡器组成。通过判断每个符号周期内接收到的信号是否与混沌振荡器同步，即可解调出有用信息。混沌调制通信的原理是在发送端将待传输的信息调制到混沌系统的参数中，在接收端通过混沌系统实现同步，恢复出混沌系统的参数，从而解调出有用信息。

格日博夫斯基等人 [15]通过研究统一混沌系统的最优线性反馈同步及其在密码学中的可能应用，提出了一种基于混沌的加密算法。王等人 [16]通过使用非线性耦合方法实现了两个耦合映射格子的同步。任和白 [17]提出了一种基于时空混沌的安全通信新方法。娜娜和沃福 [18]研究了利用三个耦合振荡器实现信息传输的可行性。王等人 [19]利用由随机序列控制的混沌生成策略构建了一个高维数字混沌系统。瓦伊德亚纳坦等人 [20]提出了一种具有三个二次非线性项的十一项四维超混沌系统。为了验证理论模型的可行性，详细介绍了基于SPICE的四维超混沌系统的电子电路实现。在[21], 提出了一种基于载波加密和典型数据加密技术的安全加密系统，并将其应用于噪声公共信道中的安全通信。在 [22], 利用麦克斯韦‐布洛赫方程开发的五维常微分方程系统被用来解释半导体激光器的动力学行为。卡西姆等人 [23]开发了一种基于分数阶离散时间超混沌系统同步的图像传输安全方案。奥登等人 [24]提出了一种基于混沌光相位载波的混沌通信方案，该载波由具有非线性时延反馈的光电振荡器产生。在 [25, 26]提出了超混沌系统并研究了其动力学特性。在 [27–29], 描述了混沌超加速度系统。通过分析其平衡点、耗散性、分岔图和李雅普诺夫指数，证明了其混沌动态特性。设计了模拟电子电路以验证其在安全通信中的可行性。在 [30], 提出了一种新型五维超混沌四翼忆阻系统，并将其应用于现场可编程门阵列（FPGA）中的安全通信。在 [31–33]华中云、周一聪等人发现了将低维混沌系统应用于电子对抗措施（ECM）、多载波系统（MCS）和现场可编程门阵列（FPGA）领域的一些优秀方法。在 [34]开发了一种基于六维实域混沌的视频加密解密通信方法。此外，系统设计和算法分析通过在FPGA硬件平台上使用Verilog硬件描述语言进行验证。由于传统多级频移键控混沌移键中存在大量延迟线和正交沃尔什码序列，李等人 [35]提出了一种新的高效多级频移键控混沌移键通信系统。阿希克和阿米萨拉詹 [36]宣布了一种基于频域混沌吸引子并通过整数小波变换（IWT）与空间域脱氧核糖核酸（DNA）序列混合的DICOM图像加密方法。

2 五维超混沌系统分析

2.1 五维超混沌系统的构造

本文设计了一种新的五维超混沌系统：
$$
\begin{cases}
\dot{x} = ax + by + cu \
\dot{y} = dx - xz + u - y + iw \
\dot{z} = xy - fz \
\dot{u} = gx + w \
\dot{w} = mxy - lw
\end{cases}
$$
其中 $ a = -25 $, $ b = 25 $, $ c = 1.3 $, $ d = 35 $, $ i = 2 $, $ f = 4 $, $ g = -8 $, $ m = -0.8 $, $ l = 5 $。李雅普诺夫指数为 $ Ly_1 = 0.17826 $, $ Ly_2 = 0.110013 $, $ Ly_3 = 0 $, $ Ly_4 = -5.18539 $, $ Ly_5 = -28.108 $。从李雅普诺夫指数的角度来看，该系统的李雅普诺夫指数有两个正值、一个零值和两个负值。李雅普诺夫指数之和为 $ Ly = -33.0051 $，小于零，符合李雅普诺夫指数的判定规则。因此，系统当前处于超混沌状态。x、y、z、u和w之间的相图如图1所示。

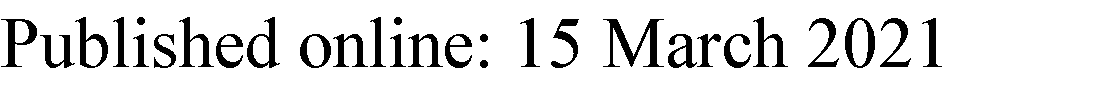
2.2 五维超混沌系统的动态分析

生成超混沌系统需要满足两个必要条件：（1）对于混沌系统，系统的维数至少为4；（2）存在至少两个正李雅普诺夫指数，且所有李雅普诺夫指数的和小于零。

五维超混沌系统的雅可比矩阵如下所示：
$$
Jac =
\begin{bmatrix}
-25 & 25 & 0 & 1.3 & 0 \
35-z & -1 & -x & 1 & 2 \
y & x & -4 & 0 & 0 \
-8 & 0 & 0 & 0 & 1 \
-0.8y & -0.8x & 0 & 0 & -5
\end{bmatrix}
$$

李雅普诺夫指数和分岔是分析和判断超混沌的两种有效工具。对于超混沌和混沌而言，李雅普诺夫指数是必需的，它表明轨道的发散率不同。分岔是一种与超混沌、混沌及参数变化相关的特殊非线性现象。分岔图通过参数的最大值获得。对于该五维超混沌系统，当其他参数固定时 $ a = -25 $, $ b = 25 $, $ c = 1.3 $, $ d = 35 $, $ i = 2 $, $ g = -8 $, $ m = -0.8 $, $ l = 5 $，初始条件为 $ x_0 = 1 $, $ y_0 = 1 $, $ z_0 = 1 $, $ u_0 = 1 $, $ w_0 = 1 $，线性控制系数 $ f \in [0, 20] $ 的李雅普诺夫指数谱和分岔图如图2所示。同时，图2b展示了图2a中李雅普诺夫指数谱部分的放大视图。

随着参数的变化，系统平衡点的稳定性发生变化，因此系统处于不同的状态。李雅普诺夫指数可用于比较和分析系统参数变化时系统状态的改变。为了评估所设计的五维超混沌系统的有效性，本文详细介绍了系统的四种非线性状态。当 $ 0 < f < 0.65 $ 时，系统具有一个零李雅普诺夫指数，四个负李雅普诺夫指数，系统处于周期状态。当 $ 0.65 < f < 6 $ 时，系统具有两个正李雅普诺夫指数、一个零李雅普诺夫指数和两个负李雅普诺夫指数，系统处于超混沌状态。当 $ 6 < f < 7.6 $ 时，系统具有一个正李雅普诺夫指数、两个零李雅普诺夫指数和两个负李雅普诺夫指数，系统处于混沌状态。当 $ 7.6 < f < 8.5 $ 时，系统具有一个零李雅普诺夫指数和四个负李雅普诺夫指数，系统处于周期状态。

2.2.1 周期性

固定参数为 $ a = -25 $, $ b = 25 $, $ c = 1.3 $, $ d = 35 $, $ i = 2 $, $ g = -8 $, $ m = -0.8 $, $ l = 5 $，改变 $ f $，当 $ 0 < f < 0.65 $ 时，新的五维系统处于周期状态。相图如图3所示，其中 $ f = 0.1 $。根据计算，此时的李雅普诺夫指数为 $ Ly_1 = 0 $, $ Ly_2 = -0.096162 $, $ Ly_3 = -0.315006 $, $ Ly_4 = -5.457413 $, $ Ly_5 = -25.224891 $。李雅普诺夫指数之和为 $ Ly = -31.093472 $，小于零。该系统明显处于周期状态。

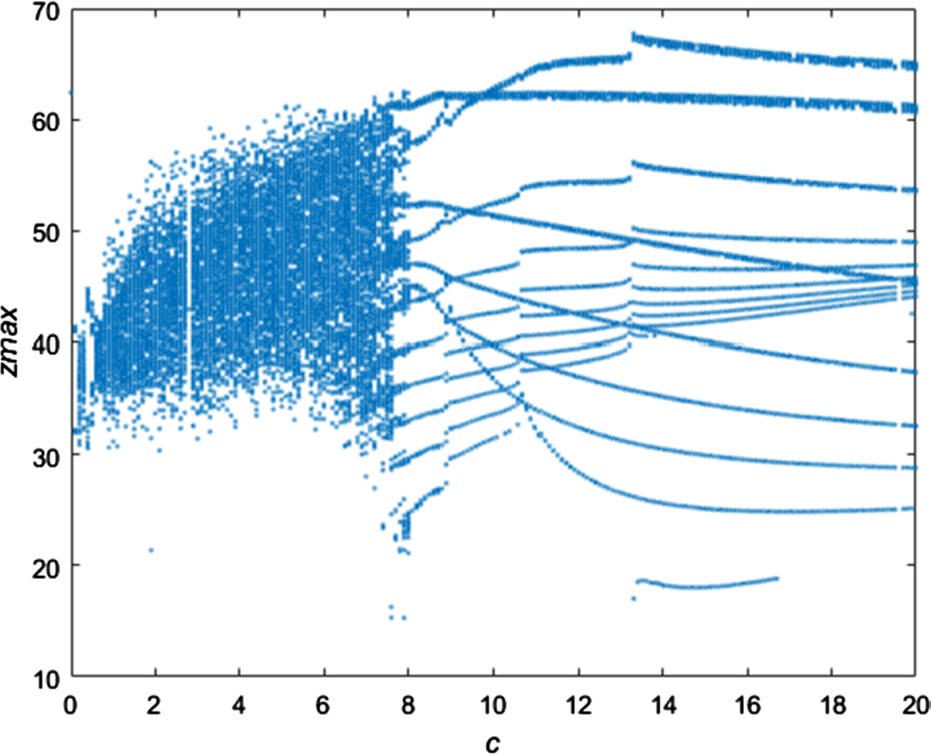
固定参数 $ a = -25 $、$ b = 25 $、$ c = 1.3 $、$ d = 35 $、$ i = 2 $、$ g = -8 $、$ m = -0.8 $、$ l = 5 $，改变 $ f $，当 $ 8.5 < f < 20 $ 时，新的五维系统处于周期状态。当 $ f = 19 $ 时的相图如图4所示。根据计算，此时的李雅普诺夫指数为 $ Ly_1 = 0 $、$ Ly_2 = -2.897683 $、$ Ly_3 = -3.830672 $、$ Ly_4 = -4.992414 $、$ Ly_5 = -38.285422 $。李雅普诺夫指数之和为 $ Ly = -50.006208 $，小于零。该系统显然处于周期状态。

中部分李雅普诺夫指数谱的放大视图；c 分岔图)

2.2.2 超混沌

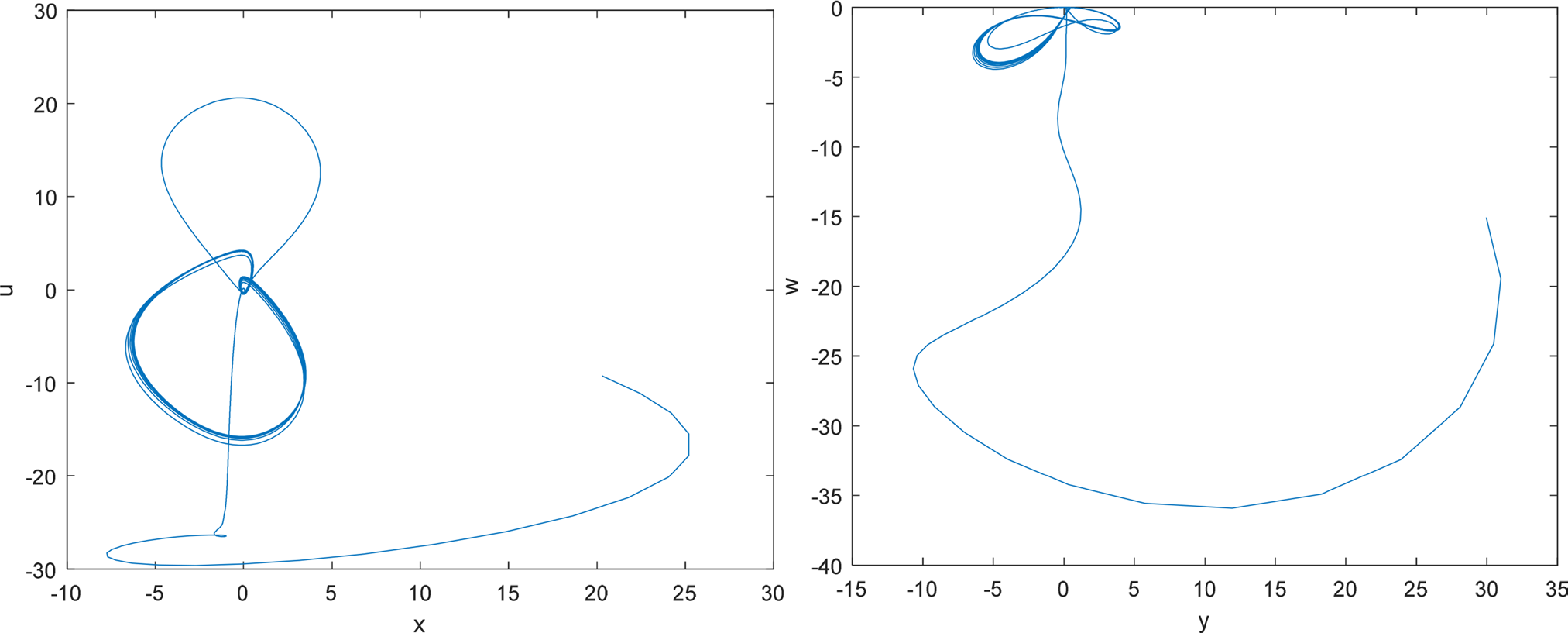
固定参数 $ a = -25 $、$ b = 25 $、$ c = 1.3 $、$ d = 35 $、$ i = 2 $、$ g = -8 $、$ m = -0.8 $、$ l = 5 $，改变 $ f $，当 $ 0.65 < f < 6 $ 时，新的五维系统处于稳定定点状态。当 $ f = 4 $ 时，相图如图5所示。根据计算，此时的李雅普诺夫指数为 $ Ly_1 = 0.319611 $、$ Ly_2 = 0.268729 $、$ Ly_3 = 0 $、$ Ly_4 = -5.065125 $、$ Ly_5 = -30.527872 $。李雅普诺夫指数之和为 $ Ly = -35.0047 $，小于零。该系统显然处于超混沌状态。

2.2.3 混沌

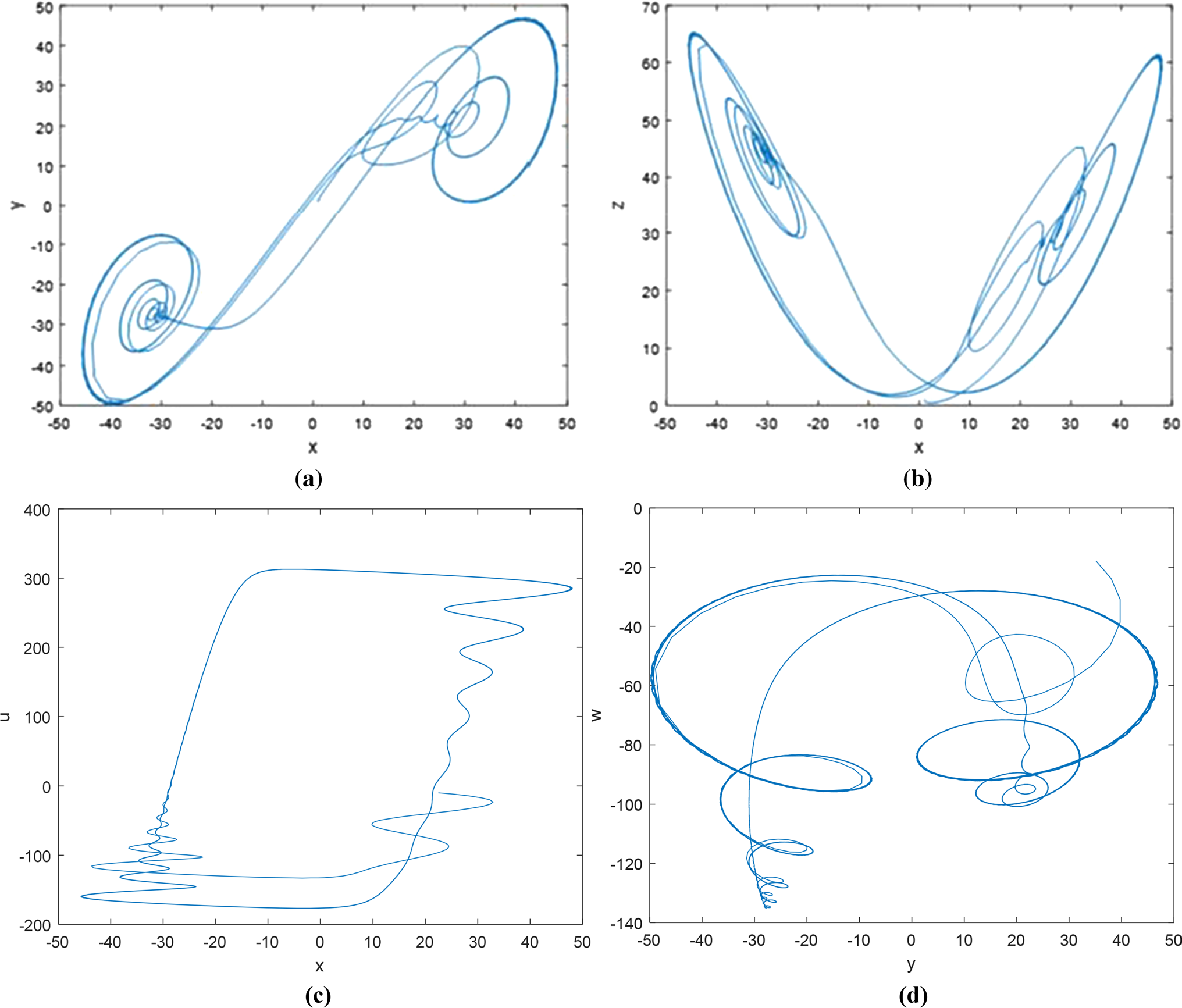
固定参数 $ a = -25 $，$ b = 25 $，$ c = 1.3 $，$ d = 35 $，$ i = 2 $，$ g = -8 $，$ m = -0.8 $，$ l = 5 $，改变 $ f $，当 $ 6 < f < 7.6 $ 时，新的五维系统处于混沌状态。当 $ f = 7 $ 时的相图如图6所示。根据计算，此时的李雅普诺夫指数为 $ Ly_1 = 0.184618 $，$ Ly_2 = 0 $，$ Ly_3 = -0.021131 $，$ Ly_4 = -4.877598 $，$ Ly_5 = -33.335183 $。李雅普诺夫指数之和为 $ Ly = -38.0493 $，小于零。该系统明显处于混沌状态。

2.3 复杂度测量分析

混沌系统的复杂度是指混沌序列通过相关算法衡量其接近随机序列的程度，复杂度值越大，序列越接近随机序列，相应的安全性越高。本文采用SE复杂度和C0复杂度对所提出的超混沌系统进行分析，以将具有强复杂度的区域应用于加密。

因此，我们计算了SE复杂度和C0复杂度，当f从1变化到7.6时，并分析了所需的数据和判据。当其他参数固定时，新五维系统各维度间的SE复杂度和C0复杂度如图7所示。$ a = -25 $, $ b = 25 $, $ c = 1.3 $, $ d = 35 $, $ i = 2 $, $ g = -8 $, $ m = -0.8 $, $ l = 5 $ 和初始条件为 $ x_0 = 1 $, $ y_0 = 1 $, $ z_0 = 1 $, $ u_0 = 1 $, $ w_0 = 1 $。

当系统随参数C0变化时的复杂度结果如图f所示，见图7a, c, e, g。当参数C0在1到7.6之间变化且系统处于从混沌到超混沌的状态时，五维超混沌系统的每一维复杂度剧烈波动并迅速增加，这与李雅普诺夫指数的测量结果相似。当参数f在1到7.6之间时，系统始终处于超混沌状态，且每一维的SE复杂度几乎不增加也不减少。

可以发现，Y维度的C0复杂度明显大于其他三个维度系统参数f变化时。特别是当 $ f = 4 $，$ C0_X = 0.24 $，$ C0_Y = 0.2664 $，$ C0_Z = 0.0684 $，$ C0_U = 0.0989 $。

通过对比系统参数f变化时各维度的SE复杂度结果可知，各维度的SE复杂度几乎都处于0.5至0.65之间。各维度之间的SE复杂度差异不像C0复杂度那样大，但从图7b、d、f、h中可以看出，当系统参数f变化时，五维超混沌系统中Y维度的SE复杂度几乎是五个维度中最高的。特别是当 $ f = 4 $ 时，$ SE_X = 0.5885 $，$ SE_Y = 0.6058 $，$ SE_Z = 0.5633 $，$ SE_U = 0.5183 $。根据系统参数变化时SE复杂度和C0复杂度的结果，证明了我们所提出的系统选择是正确的。

根据综合分析，当系统参数f取值在1到7之间时，系统的SE复杂度和C0复杂度变化较小。因此，当系统参数 $ f = 4 $ 时，经过复杂度分析可认为是合理的。同时，在加密时选择Y维度的时间序列是最优选择。

3 硬件电路设计

3.1 硬件选型

从上述理论可以看出，硬件主要包括单片机最小系统、加密电路、解密电路和数模转换器（DAC）电路。进一步分析表明，我们需要选择单片机、运算放大器和DAC芯片。

3.1.1 加密和解密电路

本文的基本原理是：复杂信号发生器为整个安全通信电路提供初始信号Q，该信号Q为方波电压信号。驱动电路向加密电路提供五维混沌信号Y，加密电路将信号Q与信号Y相加，因此驱动电路产生的超混沌信号Y对需要加密的信号Q进行掩蔽，加密电路输出加密信号Q1至解密电路，响应电路为解密电路提供五维混沌信号Y1, Q1，Y1由解密电路叠加，因此响应电路产生的五维混沌信号Y1抵消了加密信号Q1中的信号Y，解密电路的输出端输出解密信号Q2。该解密信号Q2与加密前的原始信号Q基本相同。

本文设计了一种基于驱动‐响应同步的方法来实现同步效果。在电路中，使用了两个反向加法电路来实现同步效果。如图8所示，原始信号OS在中央控制端单片机产生的混沌序列作用下，通过第一反向加法电路进行掩码，生成加密信号ES。当传输至解密端时，该加密原始信号和解密端单片机生成的同步混沌序列DE在第二反向加法电路中进行解密，得到解密信号DS。

3.2 Proteus仿真的总体电路图

图9显示了Proteus仿真的总体电路图。本文中，使用方波信号发生器来模拟原始信号以及中央计算机生成的控制信号。方波信号发生器产生原始信号OS。按钮模拟中央计算机处控制信号传输的开关信号，并控制控制信号的传输和生成时间。按下按钮后，单片机接收到信息并生成混沌序列，然后通过单片机的输入/输出端口输出至DAC1208进行数模转换，转换为模拟混沌信号CS。随后，在中央控制端，原始信号OS通过第一反向加法电路被单片机生成的混沌序列掩码，生成加密信号ES。当传输到接收器时，单片机接收到信息并生成混沌序列，然后通过单片机的输入/输出端口输出至DAC1208进行数模转换，转换为模拟解密信号DE。加密信号与单片机产生的同步混沌序列进行解密在第二反向加法电路中得到解密信号DS。如果解密信号DS与原始信号OS基本相同，则可以证明实验成功。

Proteus 中没有 STC15F2K60S2 的仿真模型，但 STC15F2K60S2 的内核是 8051，因此在 Proteus 中使用 AT89C51 进行仿真是相同的。

4 软件设计

4.1 单片机中混沌精度的调整与采样

考虑到单片机和DAC芯片的运算精度，有必要对我们提出的五维超混沌系统进行精度简化。由于单片机的计算精度不足，且实现高精度计算的成本过高而失去实际价值，因此在单片机中无法或难以实现ODE45算法。

欧拉算法可以极大地降低单片机生成混沌的成本，使得混沌在单片机中具有实现价值。同时，考虑到单片机的精度，需将小数位简化为两位小数，因此在单片机中实现具有理论依据。

图10显示了调整后某一时刻变量的具体值。x的值是X维五维超混沌混沌序列，而xx是调整后x的对应值。我们使用浮点数与整数的相互转换来调整X维五维超混沌混沌序列的精度，xx是精确到x两位小数的值；类似地，y的值是yy维五维超混沌混沌序列，且yy是调整后y的对应值。我们使用浮点数与整数的相互转换来调整Y维五维超混沌混沌序列的精度，yy是y精确到两位小数的值；z的值是Z维五维超混沌混沌序列，且zz是z调整后的对应值。我们使用浮点数与整数的相互转换来调整Z维五维超混沌混沌序列的精度，zz是z精确到两位小数的值；u的值是U维五维超混沌混沌序列，且uu是u调整后的对应值。我们使用浮点数与整数的相互转换来调整U维五维超混沌混沌序列的精度，uu是u精确到两位小数的值。

混沌序列经过精度调整后的值即为我们要使用的值，分别为xx、yy、zz和uu。由于混沌系统是在单片机中进行计算的，且混沌系统的小数位精确到两位小数，因此我们需要再次判断其是否为混沌。我们对yy的值进行了采样并分析，在Keil的监控页面中对变量yy的值进行迭代，取出4000个点进行判断和分析。

4.2 单片机实现的理论研究

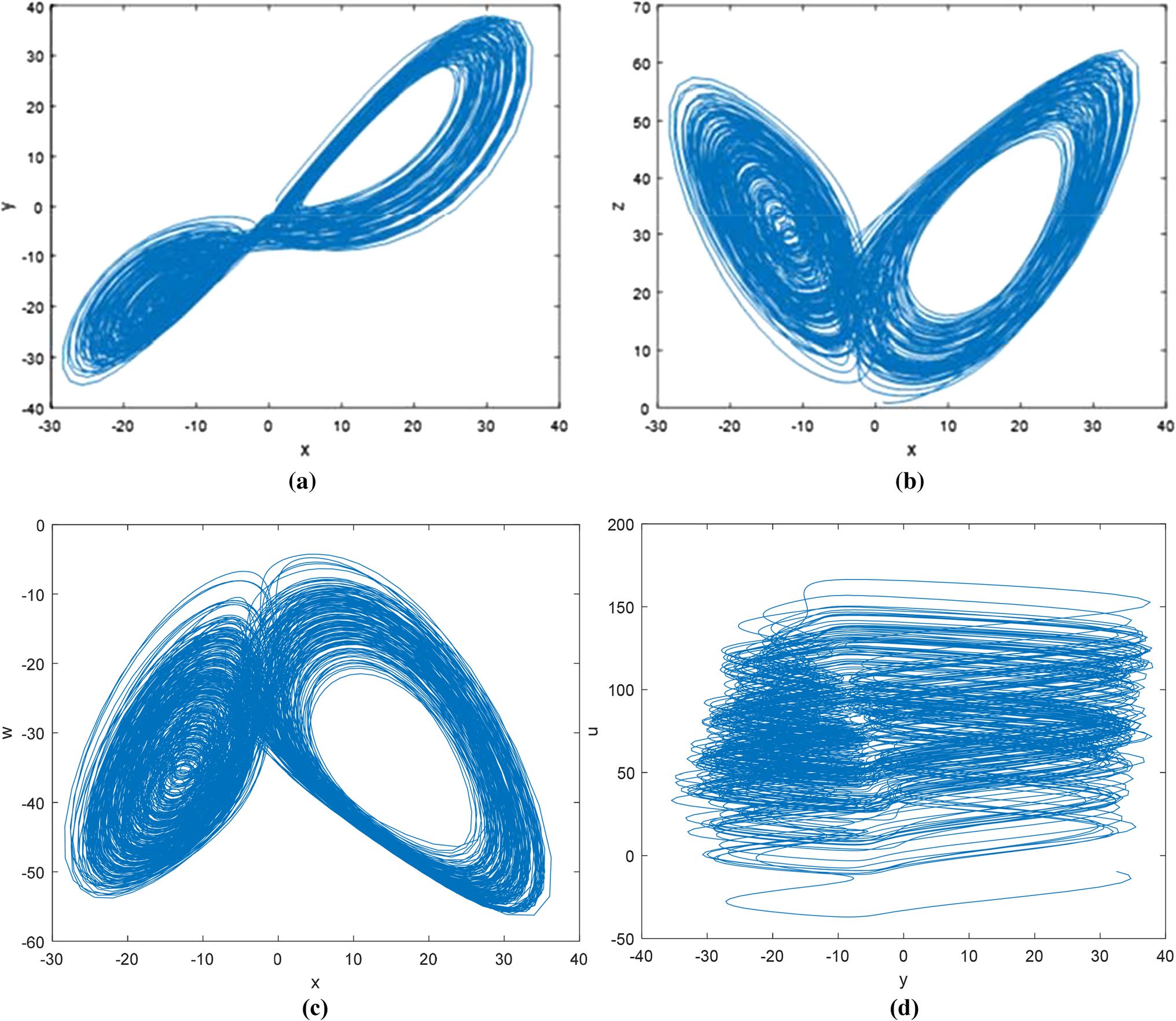
算法和小数位的改变会影响新的五维超混沌系统。因为混沌对初值极为敏感，所以这两个系统不是同一个系统。对于数据的严格要求，在改变算法后需要重新判断时间序列是否为混沌。图11显示了在Keil中改变算法并累积到两位小数后的系统相图。

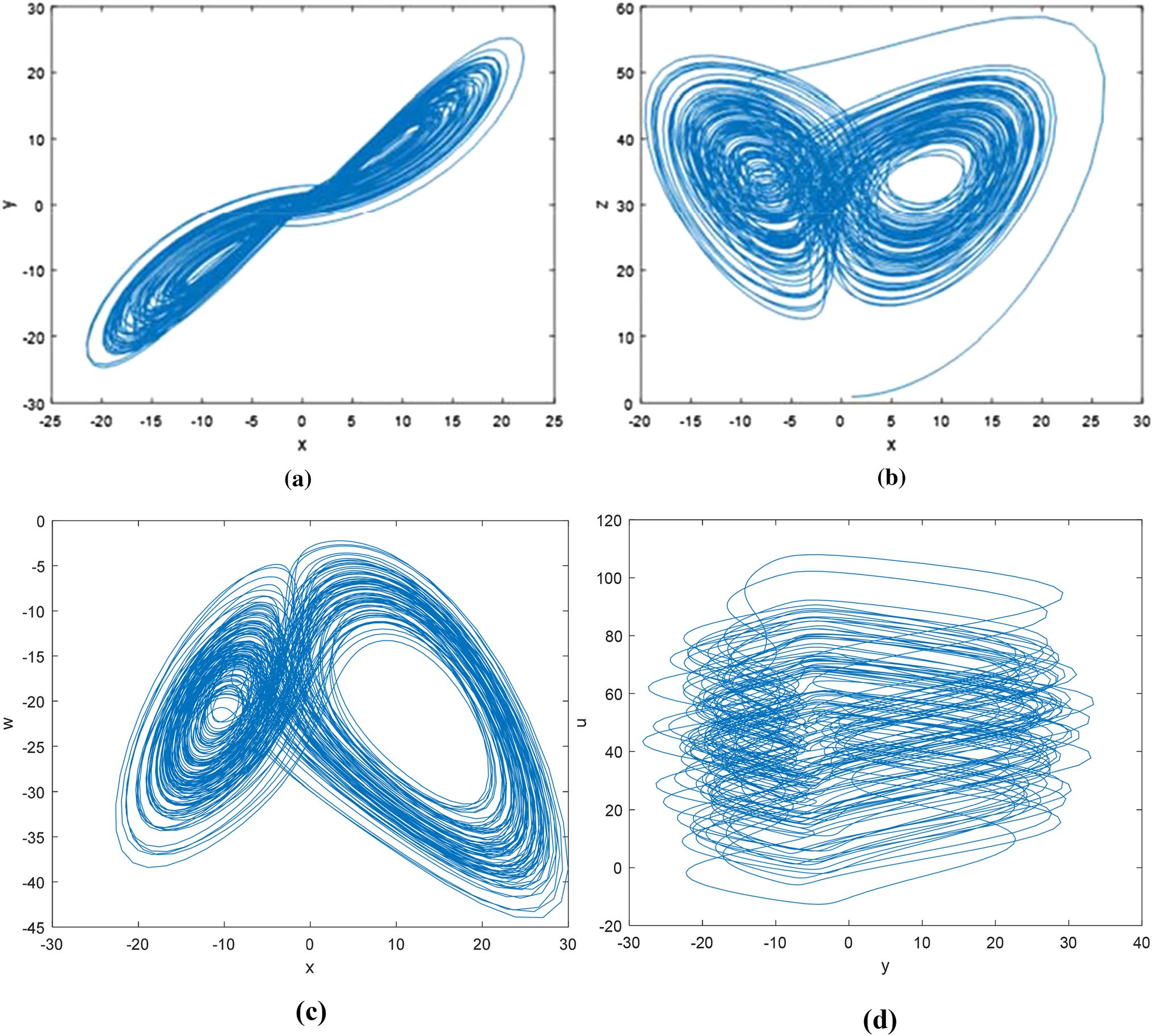
4.3 0‐1检验

是否为混沌将通过在Keil中仿真的提取数据再次判断。由于我们在加密混沌序列时仅使用复杂度最高的Y维度，因此我们所使用并需判断的数据是一组单维度的数据。

对于一维离散数据，常用的混沌判别方法如李雅普诺夫指数和庞加莱映射无法确定其是否为混沌，因此需要采用近年来发展的0‐1检验来判断一维离散数据。

当系统参数为 $ a = -25 $, $ b = 25 $, $ c = 1.3 $, $ d = 35 $, $ i = 2 $, $ f = 4 $, $ g = -8 $, $ m = -8 $, $ l = 5 $ 时，通过0‐1检验，五维超混沌系统的中值分别为 $ K_x = 0.9952 $（确认为“1”）、$ K_y = 0.9968 $（确认为“1”）、$ K_z = 0.9953 $（确认为“1”）、$ K_u = 0.9848 $（确认为“1”）和 $ K_w = 0.9960 $（确认为“1”），该五维超混沌系统处于混沌状态。图12显示 $ p_c(n)–q_c(n) $ 轨迹图、$ M_c(n)–n $ 图和 $ K_c–c $ 散点图，当 $ N = 4000 $ 且系统参数为 $ a = -25 $、$ b = 25 $、$ c = 2 $、$ d = 35 $、$ f = 3 $、$ g = -8 $ 时。由于本文仅使用Y维数据，因此仅给出Y维混沌序列的0‐1检验图。图12a显示了五维超混沌系统的 $ p_c(n)–q_c(n) $ 轨迹图。图12c显示了任意正数c随异步增长率k的变化曲线，最终值K为 $ K_c $ 的中值。由图可知，大多数线性增长率 $ K_c $ 接近1。从图12可以看出，系统的 $ p_c(n)–q_c(n) $ 类似于无界布朗运动，$ M_c(n) $ 随时间线性增长，且所有k均接近1，证明该系统是混沌的。

–q(n)；b M(n)–n；c Kc–c)

4.4 单片机输入/输出与DAC芯片输入的相应调整

由于DAC1208是一个12位DAC芯片，DAC芯片的最大值为4096。从图1可以看出，我们所使用的Y维混沌序列的最大值和最小值分别为40和−40，两者差值为80。考虑到混沌序列与最大值和最小值之间仍存在一定差异，因此可以保留两位小数。将混沌序列缩小一次并保留两位小数，再放大一百倍，可使数值差值控制在4000以下。同时，控制信号可以插入到混沌序列的实际值与最大值和最小值。

DAC1208只能输出正电压，混沌系统的负部分无法直接输出，因此需要进行调整。我们采用整体上移调整的方法，以2048为零点，高于2048的部分为正值，低于2048的部分为负值。具体步骤是：首先将混沌序列放大100倍，然后在保留整数后缩小一次，确保数值在0到4096之间，小于DAC1208的最大值4096；第二步是将混沌序列的每个值加上2048，实现整体上移调整；最后，通过C语言的逻辑与以及直接数字传输，将系统的12位混沌序列值拆分为一个4位和一个8位数据，分别通过P1和P2传输给DAC1208。

数模转换器输入变量图如图13所示，YZ为 $ 0 \times 0856 $，转换为十进制数是2155。将2155除以4096再乘以8000的结果为4208.98，这相当于逆运算。然后减去4000得到208.98，在数模转换器中，YY值的100倍。因此程序的正确性得到了验证。

5 实验结果与总结

5.1 Proteus仿真结果

实验结果如图13和14所示。图13显示了原始信号和加密信号，图14显示了在Proteus中的仿真结果。第一条黄色线是方波发生器产生的原始信号，将方波信号作为原始信号。第二条白色线是加密信号。从图中可以看出，加密信号是混乱的，因此加密成功。第三条绿色线是解密后的信号，它几乎与原始信号除存在微小毛刺外，基本无失真。由于信息接收依据高低电平判断，该毛刺不影响信息的接收。

这证明了我们的实验成功实现了安全通信，表明所设计的五维超混沌系统具有复杂的动态特性，可用于安全通信。当其应用于安全通信时，将显著提高信号传输安全性，并大幅增强抗攻击能力。电路中未使用电容器进行滤波，导致电压滞后于电流。经过放大器两次运算后产生自激振荡，从而在电压中引入微小毛刺。然而，结果仍能证明解密信号与原始信号基本一致，说明混沌电路系统已成功完成对方波电压信号的加密和解密过程。

然而，基于单片机的五维超混沌安全通信系统存在一些局限性。例如，单片机中的浮点运算速度很慢，导致混淆时间较长。本文中该时间可以接受，也可采用增强型8051内核或ARM内核单片机来提升速度。

6 结论

本文提出了一种基于单片机的五维超混沌安全通信系统。首先，分析了系统的平衡点稳定性与李雅普诺夫指数。分析结果表明，系统的周期性、超混沌和混沌状态会随参数变化而变化。然后，通过复杂度分析验证了所提系统的正确性。在调整系统的精度和算法后，通过在设计的单片机硬件电路上进行仿真，成功实现了混沌。最后，通过对单片机计算的数据验证，表明系统在调整后仍处于混沌状态。该五维超混沌系统通过单片机实现对信号的加密和解密。目前，已有大量工作利用现场可编程门阵列（FPGA）和数字信号处理器（DSP）实现混沌，但关于使用单片机实现混沌安全通信的研究较少。本文提出的基于单片机的五维超混沌系统已成功实现并具备可实施性。由于其复杂的动态特性，该系统已被广泛应用于安全通信领域，显著提高了信息传输过程的安全性。