二、大模型原理：图文解析Transformer原理与代码

Transformer是很多大模型的基石，也是现在llm面试岗位必考的。
即使是ChatGPT中的"T"也代表着Transformer。以下模型都是Transformer的演变模型（当然每个大模型的Transformer都可能存在差别）：

本文将从原理+实战带你深入理解Transformer

Transformer结构

先放出整体架构，后文的1~4点都是对原件进行深入探讨的。

从总体上来看
可以将Transformer看为是N个编码结构和N个解码结构的模型，这里的解码/编码结构即为后文解释的 Transformer Block；

上图的inputs其实是输入的embedding向量+位置编码向量。

1. Token Embedding：从符号到向量的转换

上一小节我们已经讲述了一句话是如何转为数值表达的，但对于计算机而言仅仅是一个个数值是没有语义信息的。

Token本质上是符号：

• "Apple"是一个符号
• "Cat"是一个符号
• "Run"是一个符号
• "Jump"是一个符号

虽然我们知道"Run"和"Jump"都是动词，它们在语义上比"Cat"和"Apple"更相近，但从Token的角度看，它们都只是独立的符号，彼此之间没有任何关联。

实现机制：查表法

Transformer中的Token嵌入采用查表法：

1. 维护一个包含所有可能Token及其对应向量的表格
2. 对于每个输入Token，在表中查找其对应的向量
3. 这些向量是模型的可学习参数，在训练过程中自动优化

2. 位置编码：为序列添加位置信息

需要位置编码原因可以回想一下RNN，对RNN而言是用的一套参数。
而Transformer的输入是一起扔给模型的，因此就缺少了先后位置关系，从而使用了位置编码。

假设没有位置编码，同一个Token总是有相同的向量表示，那么模型将会丧失了对上下文的信息保留。例如：

• “Bank”（银行）在"I went to the bank"中
• “Bank”（河岸）在"I sit by the river bank"中
  这两个"bank"使用相同的Token Embedding，但含义完全不同，保留了位置信息为下面的多头注意力机制保留了所含有的信息。

位置编码的实现方式

1. 人工设计的位置嵌入

最早的Transformer实现中，位置编码是人工设计的，采用以下方式：
使用正弦和余弦函数为每个位置生成独特的编码

简单来说就是偶数位为sin，奇数位为cos。

2. 可学习的位置嵌入

位置编码也可以通过训练学习

3. 注意力机制（Attention）

通过注意力机制增加了语义的理解，解决了歧义问题（如"bank"指银行还是河岸）

如果你能记住下面这句话，就记住了注意力的本质：
👉 输入一排词向量 → 为每个词找到重要上下文 → 得到新的词向量

为每个词找到重要上下文，这部分即是量化了句子中任意两个词条之间的依赖关系。如下图将会去对输入句子做比较，即每个词之间又会对句子中所有词做比较

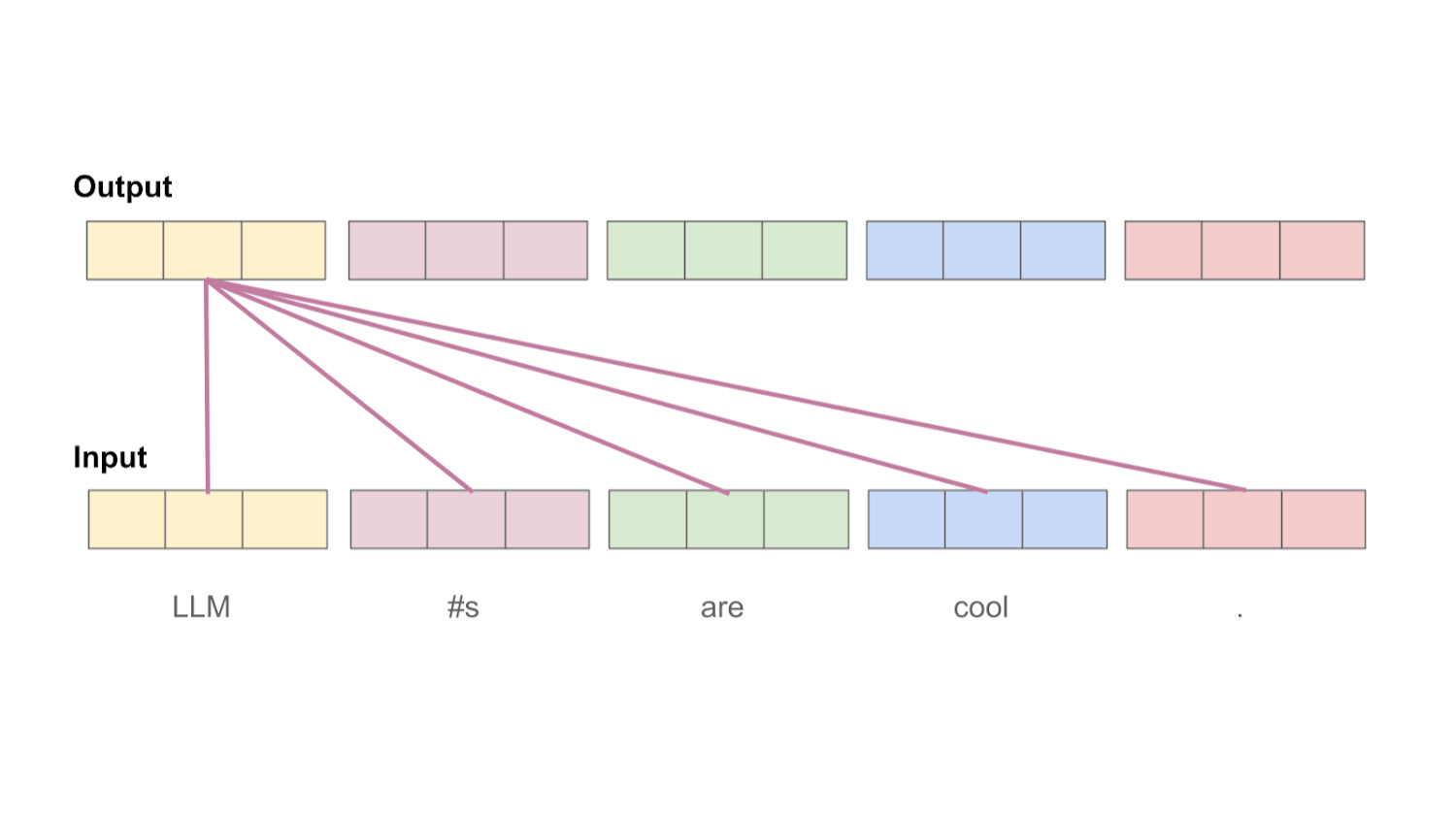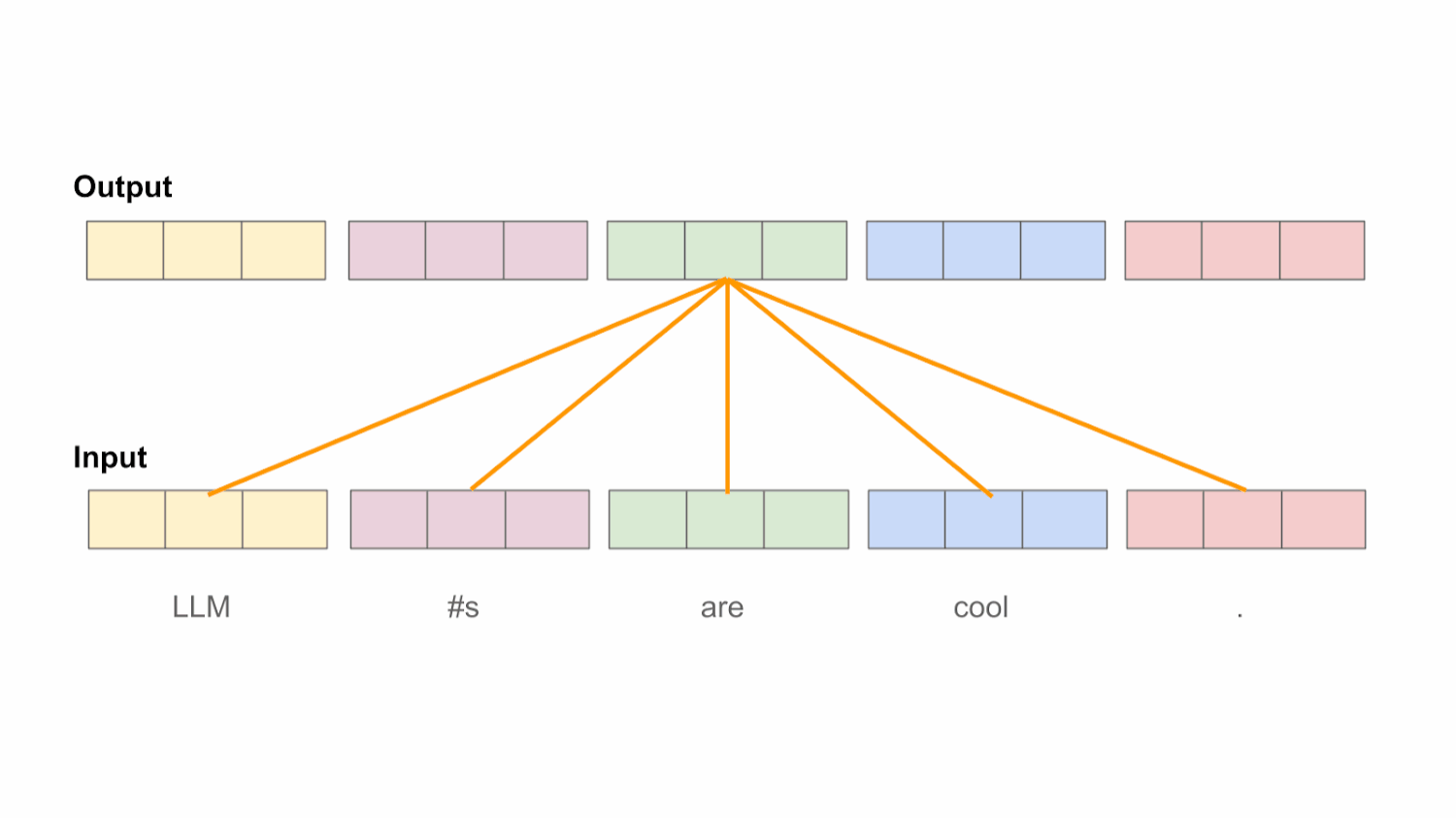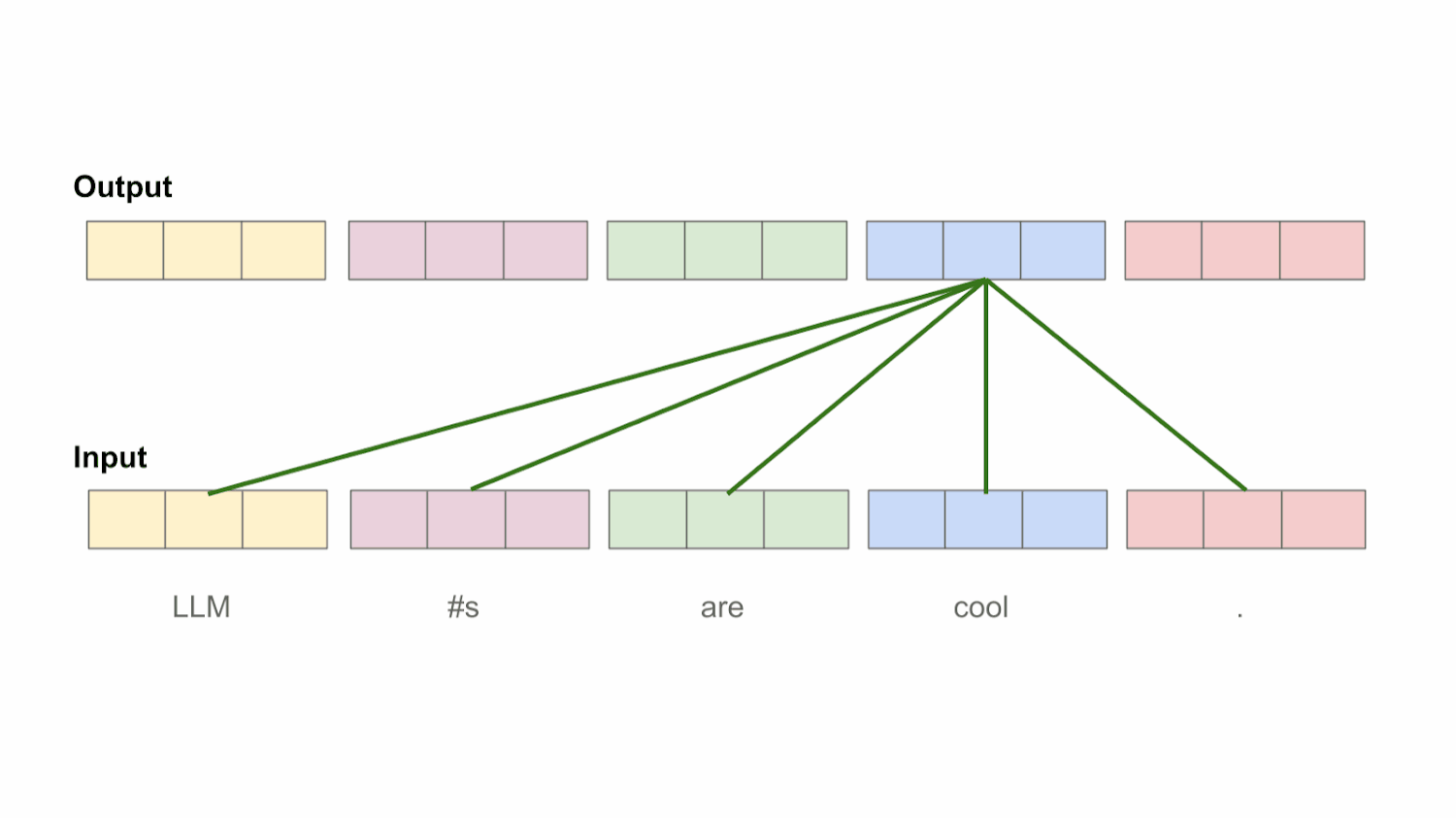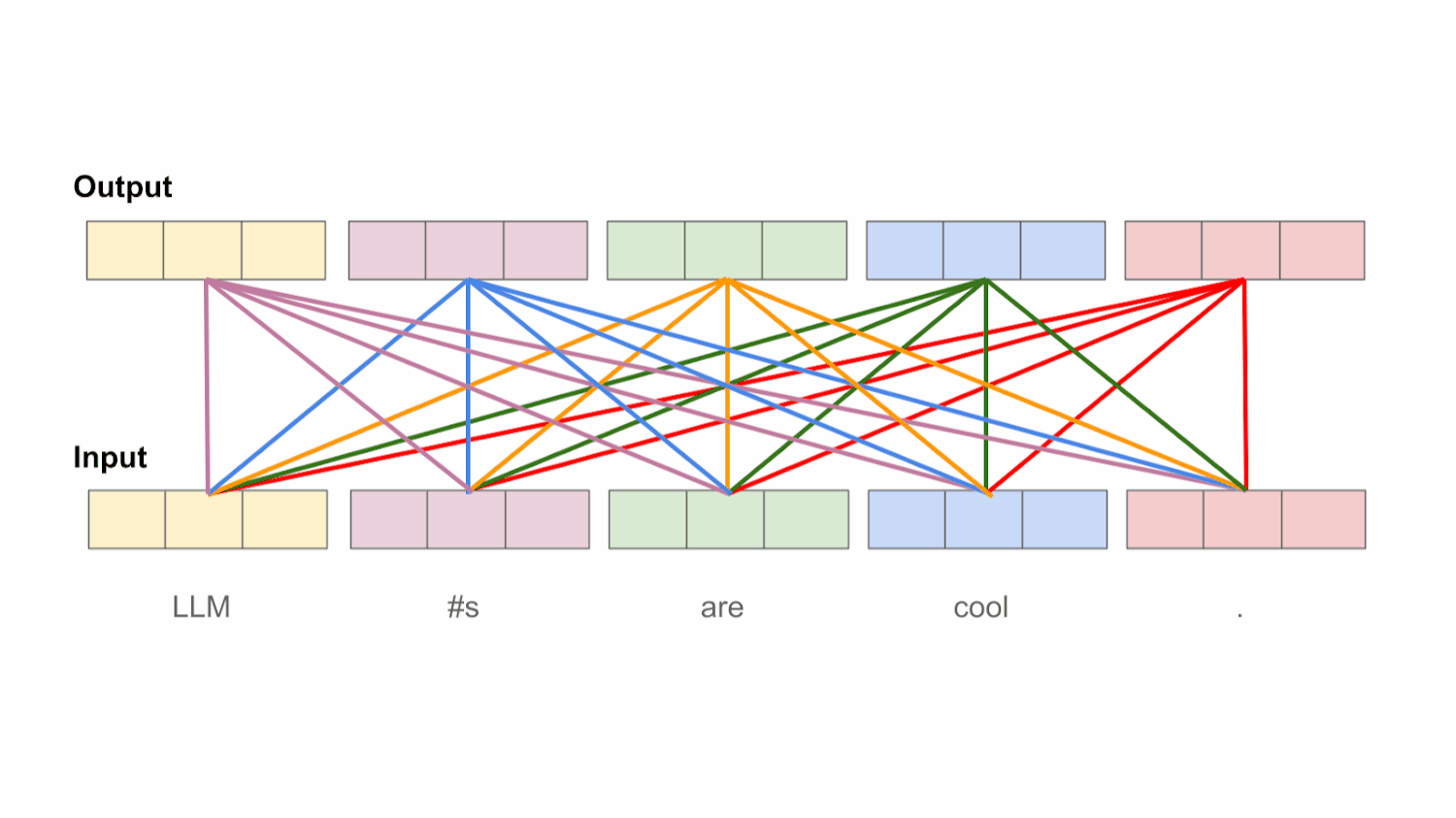
注意力机制QKV理解

注意力机制中最重要概念即对下图公式的理解

经过embedding+位置编码作为输入，我们的对模型的输入是个 $[B,T,d]$矩阵。其中批次大小为 $B$，每个序列长度为 $T$，每个词元向量的维度为 $d$，也就是自注意力层接收的输入张量形状就是 $[B,T,d]$。
为了简化说明，我们先将B设置为1，也就是单个词元序列作为输入来讲解自注意力的计算过程（见下图），但相同的原理可以很容易地扩展到多个序列组成的批次上。

QKV创建
可以看到该公式引入了三个矩阵QKV，这些矩阵来自于输入序列中的token向量，经过了三次独立的（线性）投影，形成Q、K和V矩阵。
这

以输入 [“LLM”, “#s”, “are”, “cool”]为例，每个词通过嵌入层和线性投影后得到Query向量和Key向量。
为了简化，我们假设每个向量是3列组成的（也就是head_size,这是一个由开发者决定的超参数，控制了QKV矩阵的维度，即注意力头大小)：

embeddings = [
    [0.1, 0.2, 0.3],  # "LLM"的嵌入
    [0.4, 0.5, 0.6],  # "#s"的嵌入
    [0.7, 0.8, 0.9],  # "are"的嵌入
    [1.0, 1.1, 1.2]   # "cool"的嵌入
]

投影为Query和Key矩阵
现在，我们需要用两个不同的投影矩阵将这些嵌入转换为Query和Key。
假设我们的投影矩阵是:

W_q = [
    [0.1, 0.2, 0.3],
    [0.4, 0.5, 0.6],
    [0.7, 0.8, 0.9]
]

W_k = [
    [0.9, 0.8, 0.7],
    [0.6, 0.5, 0.4],
    [0.3, 0.2, 0.1]
]

计算注意力分数
在对输入进行投影之后，会使用 Key 和 Query 向量来生成注意力分数。词之间与所有前后所有词两两组合，形成一个个词元，对每个词元进行计算注意力分数。专业点来说即是：对于序列中的每一对词元 $[i,j]$，我们都会计算一个注意力分数 $a[i,j]$。注意力分数的取值范围是 $[0,1]$，它定量地表示在计算词元 $i$ 的新表示时，词元 $j$ 应该被考虑的程度。

i（当前词）	j（参与加权的词）	计算	含义
0 (“LLM”)	0 (“LLM”)	$a[0, 0] = q_0 \cdot k_0$	“LLM” 关注自己多少
	1 (“#s”)	$a[0, 1] = q_0 \cdot k_1$	“LLM” 关注 “#s” 多少
	2 (“are”)	$a[0, 2] = q_0 \cdot k_2$	“LLM” 关注 “are” 多少
	3 (“cool”)	$a[0, 3] = q_0 \cdot k_3$	“LLM” 关注 “cool” 多少
1 (“#s”)	0 (“LLM”)	$a[1, 0] = q_1 \cdot k_0$	“#s” 关注 “LLM” 多少
	1 (“#s”)	$a[1, 1] = q_1 \cdot k_1$	“#s” 关注自己多少
	2 (“are”)	$a[1, 2] = q_1 \cdot k_2$	“#s” 关注 “are” 多少
	3 (“cool”)	$a[1, 3] = q_1 \cdot k_3$	“#s” 关注 “cool” 多少
2 (“are”)	0 (“LLM”)	$a[2, 0] = q_2 \cdot k_0$	“are” 关注 “LLM” 多少
	1 (“#s”)	$a[2, 1] = q_2 \cdot k_1$	“are” 关注 “#s” 多少
	2 (“are”)	$a[2, 2] = q_2 \cdot k_2$	“are” 关注自己多少
	3 (“cool”)	$a[2, 3] = q_2 \cdot k_3$	“are” 关注 “cool” 多少
3 (“cool”)	0 (“LLM”)	$a[3, 0] = q_3 \cdot k_0$	“cool” 关注 “LLM” 多少
	1 (“#s”)	$a[3, 1] = q_3 \cdot k_1$	“cool” 关注 “#s” 多少
	2 (“are”)	$a[3, 2] = q_3 \cdot k_2$	“cool” 关注 “are” 多少
	3 (“cool”)	$a[3, 3] = q_3 \cdot k_3$	“cool” 关注自己多少

实际计算中，我们可以通过将所有的 Query 向量和 Key 向量分别堆叠成两个矩阵