木质素提取提升纸浆厂电力灵活性

化学制浆

评估多元化副产品组合的价值以提高纸浆厂的 生产灵活性

摘要

本文提出了一个针对能源价格和蒸汽需求变化的 制浆厂蒸汽公用工程系统设计优化模型。以斯堪的纳维 亚硫酸盐浆厂为案例研究，探讨了木质素提取和新涡轮 机的投资机会。该模型能够识别出比使用关键输入数据 年均值的传统模型更具灵活性的解决方案。案例研究结 果表明，在特定条件下，如果工厂同时投资于木质素提 取和凝汽式汽轮机容量，则木质素提取具有提升制浆厂 电力生产灵活性的潜力。然而，这种电力生产的灵活性 潜力会随时间变化。在本研究的工厂中，当纸浆生产能 力提高至约130万吨/年时，该灵活性潜力估计在15至30 兆瓦之间。此外，仅投资新增凝汽式汽轮机容量似乎只 有在假设电价显著高于近年来的现货价格时才具有吸引 力。此类高电价可能出现在可交易电力证书具有明确价 值，或未来电价大幅上涨的情况下。

关键词 ：发电；能源效率；灵活性；木质素提取；蒸汽 公用系统。

引言

传统的纸浆和造纸工厂早期技术经济评估在筛选与能源 相关的投资机会时，通常仅考虑一种或少数几种运行情 景，以及燃料、电力和工厂产品的固定市场价格。对于 传统纸浆厂或造纸厂而言，由于其通常以接近设计容量 的稳定生产速率连续运行，且核心运行目标是最大化单 一产品的质量和产量，因此这种做法是合理的。

近年来，由于对可持续的生物质燃料和产品需求不 断上升，造纸工业开始转变商业模式，这一趋势受到可 再生能源目标的推动，同时也受到工业界在资源和能源 利用效率方面日益增长的压力。许多造纸厂目前正在向 森林生物炼制厂转型，除了生产纸浆和纸张外，还生产 传统的能源副产品（如电力和热能），以及生物燃料、 生物基材料和化学品（Moshkelani 等，2013年；de Blasio，2019年）。已有大量研究对这些新技术和工艺 进行了技术经济评估（参见例如 Olsson 等，2006年； Benali 等，2014年；Lundberg 等，2014年； Mesfun 等，2014年；Mansoornejad 等，2017年； Akbari 等，2018年）。然而，随着能源和产品价格、政 策工具等因素的变化，造纸工业副产品的最佳投资选项 也将随之改变。

生物炼制概念预期的好处之一是，多元化产品组合 将使工厂所有者能够应对产品市场的变化（ Mansoornejad 等人 2012）。因此，提供此类灵活性的 技术选项的价值被认为会增加。考虑到制造灵活性的潜 在好处，投资多种技术以根据市场状况优化产品组合也 可能是有益的。斯文森等人（2015）调查了关于灵活性、 可控性以及与生物炼制工艺设计相关的运行可靠性方面的现有 文献，并指出了在新型生物炼制概念的早期筛选中更充 分考虑此类可操作性方面的一些原因。

从电力系统的角度来看，一种特别值得关注的灵活 性是工业企业对电力市场潜在的需求侧响应（阿尔韦哈 格等人，2017年）。随着系统中间歇性电力生产能力占 比不断提高，对能够向电网提供平衡电力的技术需求预 计也将增长。然而，造纸厂运行调整通常较为缓慢，因 此这些工厂在调频电力市场（通常要求在接到激活指令 后15分钟内完成调节）中发挥积极作用的潜力预计有限。

然而，对电网服务（如需求侧灵活性）日益增长的需求 也将反映在日前电力现货市场上，未来该市场的电力现 货价格预计将呈现更大的价格波动。对于能够根据电力 现货价格变化调整其运行的工业企业而言，这可能带来 商业机遇。

一些先前的研究在造纸厂能源系统的决策模型中考 虑了运行灵活性。赫林等人（2017）研究了一家机械制 浆造纸厂中需求侧管理的经济潜力，假设该工厂可通过 降低纸张生产负荷来执行电力调节投标。他们的结果表 明，需求侧管理具有显著的容量，但估算出的调节电力 合理投标价格明显高于基础现货价格。在赫林等人的模 型中，运行优化是在24小时周期内进行的，因此未考虑 投资机会或季节性变化。此外，也未考虑需求变化。潘 努施卡和霍夫曼（2019）开发了一种用于化学制浆厂热 电联产系统灵活性管理的方法。他们的工厂运行优化模 型包含了热储能装置，以实现平抑蒸汽需求峰值。该模 型考虑了8天周期内热力和电力需求的逐小时变化，但未 考虑能源价格的变化和季节性需求变化。因此，此类模 型无法用于优化制浆厂能源系统的投资。西托宁和艾蒂 拉（2010）研究了波动的碳价格对造纸厂能源投资的影 响，并表明其经济价值可能十分显著。然而，西托宁和 艾蒂拉仅考虑了外部市场参数的变化，并未对过程变化。Cakembergh‐Mas 等人（2010）建立了一 个模型，用于评估硫酸盐浆厂中不同改造项目的经济效 益，并考虑了具有变化的蒸汽需求和价格的月度规划周 期。然而，他们的模型仅考虑了各种预定义配置的运行 效益。新设备的容量和投资成本仅在优化之后计算，且 未包含更短期的变化。

一个节能型市场硫酸盐浆厂通常会有过量的能源可 用于燃烧黑液。可再生能源发电的政策激励（托洛兰德 和奥托松 2008，埃里克松等 2011）促使斯堪的纳维亚 地区的多家市场硫酸盐浆厂投资建设凝汽式汽轮机以进 行电力生产。其他替代性和竞争性技术与工艺解决方案 也日益受到关注。在最近的一篇文章中，阿克巴里等 （2018）比较了将黑液转化为高附加值产品的不同方案， 并发现对于加拿大纸浆厂而言，提取木质素作为产品是 最有利可图的途径。已有多种方法被提出用于从黑液中 提取和增值木质素（参见哈布等（2019）的最新综述）。

LignoBoost 工艺是此类木质素提取技术中最成熟的技术 之一，通过 CO2酸化使木质素从黑液中沉淀出来（托马 尼 2010），目前已有两家硫酸盐浆厂实现了商业化规模 运行（比约克等 2015，Wallmo 等 2016）。木质素提 取可能有助于造纸工业应对电力市场价格变化的需求侧 响应（参见例如 Jannasch 等 2019）。通过增加或减少 木质素提取量，可以调节蒸汽生产，从而调整汽轮机发 电，以应对不断变化的电价。

为了确定灵活性的价值是否足够高，以证明投资两 种或多种技术（例如，同时进行木质素提取和新增汽轮 机）的成本是合理的，必须对设计（投资）和运行决策 以及工艺和市场条件的变化进行恰当建模。这也是在考 虑变化的前提下优化设备规模所必需的。针对变化的蒸 汽需求条件下蒸汽公用工程系统的设计优化问题，通常 被表述为多周期混合整数线性规划（MILP）模型（参见 马雷沙尔和卡利文策夫 2003、商和科科西斯 2005、阿 吉拉尔等 2007、陈和林 2011、孙等 2017）。我们之前 的研究（斯文森等 2014、斯文森 2014，2015）表明，可能存在

制浆厂能源系统中某些投资的灵活性价值，以及包含投资和运行决策的多周期建模方法，适用于在投资评估中 捕捉该价值。

我们之前的研究（斯文森 2014，2015）以制浆厂蒸 汽公用工程系统的数学模型为例。该模型并不代表实际 存在的工厂，因此无法获得测量数据用于验证设备性能 模型，或识别影响系统最重要的变化因素。在该研究中， 仅考虑了蒸汽需求的季节性变化，并假设其遵循一种平 滑的连续函数，代表所研究系统类型的季节性变化规律。

实际上，除了季节性变化外，蒸汽需求变化还受到多种 因素的影响，包括生产速率差异、生产周期安排或环境 温度等。此外，这些因素不仅影响工艺蒸汽需求，还会 影响例如回收锅炉中的蒸汽生产。市场价格参数如电力 和生物质价格也随时间变化，这对系统的最优运行具有 显著影响。

在将先进的建模工具用于工业能源系统设计中的变 化分析时，应用于实际工业案例会面临诸多挑战。这些 挑战涉及数据可靠性、大量难以确定相关性的变化来源、 成本数据的不确定性、技术规格和文档资料的缺失，以 及文献模型与测量数据之间对应性较差等问题。在本文 所呈现的研究中，我们将先前开发的模型应用于一个真 实的工业案例研究。我们对模型进行了扩展，以涵盖更 多的变化来源，并识别出一系列必要的简化和改进措施， 以克服上述挑战。

本文旨在进一步开发和改进用于制浆厂蒸汽动力系 统设计优化的模型，以应用于实际工业问题。该模型用 于研究能源价格和运行条件的变化如何影响制浆厂在燃 料和电力生产方面的投资决策，以及工厂所有者对投资 增加运行灵活性的意愿。本研究以一家现代化、节能型 的斯堪的纳维亚硫酸盐浆厂为案例研究对象。所考虑的 投资包括新建木质素提取装置和新型蒸汽轮机。根据不 同的投资方案，工厂潜在的能源盈余可表现为树皮、木 质素或发电。这些措施的影响如下

通过比较在考虑变化条件时的最优投资与仅考虑单一运 行和价格情景时的最优投资，对变化进行了分析。通过 这种方法，本文还说明了木质素提取在多大程度上能够 帮助纸浆厂提高发电灵活性，以应对电力市场的日常变 化。

案例研究纸厂

本研究中的工厂是一家大型硫酸盐浆厂，纸浆年生产能 力为75万空气干燥吨。该工厂拥有一条生产线，以生产 周期方式运行。每个生产周期包括为期三周的软木生产 周期，随后是一周的硬木生产周期，即该工厂生产的纸 浆中软木浆约占75%，硬木浆约占25%。

在正常运行期间，回收锅炉产生的蒸汽不仅足以满 足工艺对蒸汽的需求，还能产生多余的热能和电力。该 工厂是电力净输出方，并向同址锯木厂和当地区域供热 网络供应多余的热能。

多年来，该工厂一直在努力改进制浆过程，以提高 纸浆质量和增加生产能力。此外，制浆过程的能源效率 也持续得到提升。例如，该工厂具有很高的工艺余热回 收程度，并已提出进一步措施，以增加二次热能用于燃 烧空气预热和锅炉给水预热。虽然纸浆仍然是核心产品， 但该工厂已逐步发展成为多产品工厂，其中电力销售对 总收入贡献显著。因此，对于该制浆公司而言，进一步 提高资源效率并开发能够最大化多种副产品 combined 收入的产品组合，已成为越来越重要的课题。

蒸汽公用系统

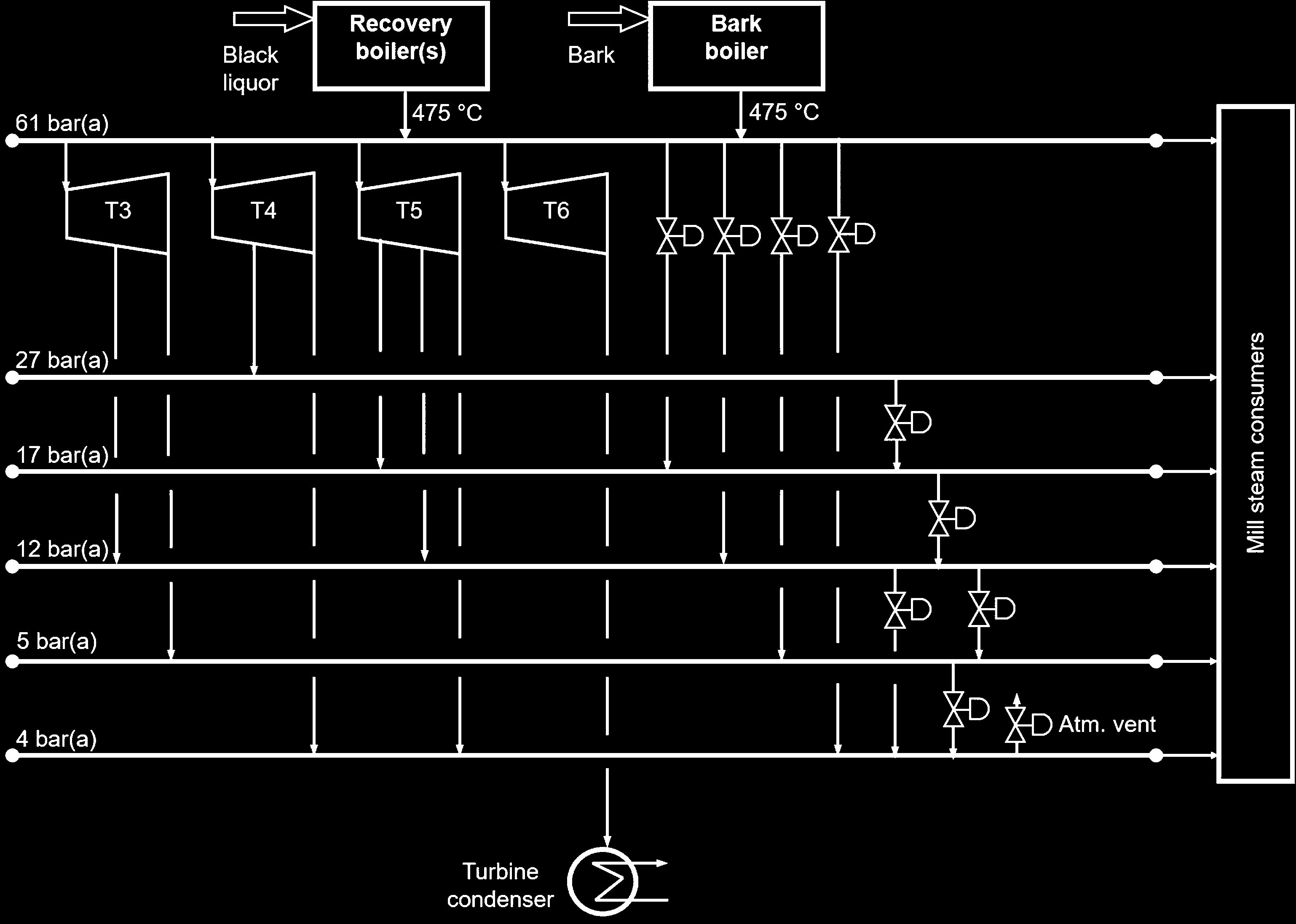
图1展示了工厂蒸汽公用系统的简化流程图。回收锅炉是 主要的蒸汽生产单元。回收锅炉中的蒸汽生产量随着时 间而变化，具体取决于黑液的流量和热值的变化（另见 制浆厂部分的工艺数据和容量约束）。在大多数运行条件下，回收锅炉的蒸汽生产足以满足工 艺蒸汽需求。然而，为了应对回收锅炉蒸汽供应的变化 以及工艺蒸汽需求的变化，管理工厂的蒸汽平衡，还持 续运行着一台以树皮为燃料的辅助锅炉。

木质素提取

本研究包含了工厂投资建设木质素提取装置的可能性。

通过在蒸发站中采用酸沉淀法从黑液中去除木质素，可 将木材原材料中的过剩能源转化为高附加值产品。提取 木质素将使制浆厂有机会生成一种新的副产品，该副产 品可用于多种用途（格尔斯特德等人，2013；特吉亚等 人，2017）。先前的研究还表明，木质素提取可能为间 接提高制浆厂公用工程系统应对蒸汽需求变化的灵活性 提供重大机遇（斯文森 2014，2015）。其作用机制在于 提供了一种调节回收锅炉负荷的方法，从而实现更宽范 围的蒸汽生产运行，而不完全依赖于在树皮锅炉容量有限的范围内。研究表明，在纸浆产量 增加的情况下，木质素提取也有助于缓解回收锅炉的瓶 颈问题（阿克塞尔松等人，2006，拉克斯梅察等人， 2009，瓦尔莫等人，2009，瓦利马基等人，2010，佩兰‐ 勒瓦瑟等人，2011）。

产量增加

纸浆厂公司正在研究一项关于新建生产线的战略投资机 会，这将显著提高纸浆生产的容量。目前正在评估新生 产线不同纸浆产品方案的可行性。我们考虑其中一种方 案，即新生产线扩展工厂当前生产的一种纸浆产品的生 产能力。然而，所有方案的纸浆产量增加幅度大致相同 （约80%）。产量增加的决策基于多项标准，其中大多 数超出了本研究的范围。因此，本研究采用了由一家咨 询公司通过电子表格计算得出的新生产线设计及其相应 的质量与能量平衡作为输入数据。关于蒸汽系统，新生 产线主要影响的是蒸汽用量

黑液处理量以及对4和12巴（绝对）蒸汽的需求（这两者 平均将增加约80%）。此外，计划更改目前使用高压蒸 汽（61巴（绝对））进行吹灰的方式，改用27巴（绝对） 蒸汽。当纸浆产量增加导致黑液热流上升时，现有的回 收锅炉将成为瓶颈。然而，工厂内仍有一台目前未运行 的旧回收锅炉，计划在产量增加的同时重新启用。但即 便如此，两台回收锅炉共同运行仍不足以应对产量增加 后高负荷生产期间的全部黑液流量。因此，计划建设一 套木质素提取装置作为解瓶颈方案。

本研究中，采用优化模型确定木质素提取装置的最 优容量，以及在黑液热能可用性和工艺蒸汽需求预设变 化情况下新汽轮机容量的最佳投资。假设纸浆产量增加 是给定的，且不受木质素提取率变化的影响（只要提取 率不低于解除回收锅炉瓶颈所需水平）。当增加木质素 提取使得回收锅炉不再成为瓶颈时，若蒸煮器、蒸发或 漂白装置等其他工艺环节也存在进一步增产的容量限制， 则该假设是合理的。此外，假设若需消除蒸汽主管道的 瓶颈，相关改造已包含在给定的纸浆生产投资计划中， 无需进一步优化。

优化模型

本研究中使用的优化模型是一个多周期混合整数线性规 划（MILP）模型。该MILP模型用于确定最优设计决策 （在木质素提取和/或新涡轮机方面的投资容量），同时 考虑在给定投资以及价格和工艺蒸汽需求变化的情况下， 蒸汽生产和汽轮机运行的最优响应。

以下章节所述的优化模型是在先前应用于工厂示例 建模的模型基础上开发的（斯文森 2014，2015）。然而， 将该优化模型应用于实际工厂时，发现需要对模型的某 些部分进行调整。这些调整旨在考虑额外的运行约束， 以及处理设备性能数据的缺失或不确定性问题，以便根据实测数据对模型进行调优。此外，经过与工厂 员工讨论后，模型排除了每日启停锅炉或汽轮机的可能 性，因为工厂员工认为，为了实现运行优化而频繁启动 和关闭锅炉、汽轮机以及木质素提取设备在技术和经济 上均不可行。

优化的目标是：
最小化 $ r \times \text{投资成本} + \text{树皮燃料成本} - \text{木质素提取收入} - \text{电力生产收入} $ (1)

其中，总投资成本InvCost通过资本回收系数r进行年金化， BarkCost表示树皮的年燃料成本，LigRev表示木质素提 取的年运行收入，ElecRev表示电力生产的年收入。该目 标通过优化投资、树皮锅炉的蒸汽产量、木质素提取率 以及通过汽轮机的蒸汽流量来实现。

投资成本

总投资成本 InvCost 可能包括对新涡轮机和木质素提取装 置的投资（公式2）。设备 $ x $ 的投资成本函数 $ Cost_x(Y_x) $ 通过分段线性函数（在 $ n $ 个线性化区间内）表示为设备 容量 $ Y_x $ 的函数（公式3）。$ C_{\text{inv},x}(i) $ 表示分段线性函数第 $ i $th 个断点处的投资成本，$ Y_x(i) $ 表示该断点处的设备容量， $ k_x(i) $ 表示 $ Y_x(i) $ 和 $ Y_x(i+ 1) $ 之间的线性斜率。二元变量 $ z_x $ 在对技术 $ x $ 进行投资时为1，否则为0。如果对技术 $ x $ 进行投资，则设备容量 $ Y_x $ 必须位于投资成本函数的有效 线性化范围内，即在第一个线性化区间的起点 $ Y_x(1) $ 和最 后一个区间的终点 $ Y_x(n + 1) $ 之间。这由公式(4)给出。

$$
\text{InvCost} = \sum_x \text{Cost}_x(Y_x) \quad (2)
$$

$$
\text{Cost} x(Y_x) =
\begin{cases}
0, & Y_x = 0 \
C {\text{inv},x}(i) + k_x(i)(Y_x - Y_x(i)), & Y_x(i) \leq Y_x < Y_x(i+1), i
\end{cases} \quad (3)
$$

$$
z_x Y_x(1) \leq Y_x \leq z_x Y_x(n+1) \quad (4)
$$

运行成本和收入

年被划分为时间段 $ t $，其持续时间为 $ dt $，代表工厂的总年 运行时间。

BarkCost 是树皮价格 $ p_{\text{bark},t} $ 以及树皮在树皮锅炉中 作为燃料的使用量 $ Q_{\text{Bark},t} $ 的年树皮成本函数，这两者在 不同时间段 $ t $ 内可能变化（公式5）。类似地，与木质素 提取 $ Q_{\text{Lig},t} $ 相关的年木质素收入 $ \text{LigRev} $ 是不同时间段内 木质素价格 $ p_{\text{lig},t} $ 的函数（公式6）。

$$
\text{BarkCost} = \sum_t dt \cdot p_{\text{bark},t} \cdot Q_{\text{Bark},t} \quad (5)
$$

$$
\text{LigRev} = \sum_t dt \cdot p_{\text{lig},t} \cdot Q_{\text{Lig},t} \quad (6)
$$

电力生产收入表示来自电力生产的年度收入，$ E_{\text{prod},t} $（公式7）。在蒸汽轮机中生产的电力，$ E_{\text{prod},t} $，可被工 厂自用，从而减少从电网购电，或售电给电网。由于锅炉 和汽轮机负荷变化引起的自用电量变化，例如空气风机和 蒸汽冷凝泵的影响，已被忽略。假设购电和售电采用相同 的电价 $ p_{\text{el},t} $。如果工厂的电力消耗数据具有与模型相同的 时间分辨率，则可通过增加一个工厂电力平衡的约束条件， 轻松调整模型以适应不同的购电/售电价格。

$$
\text{ElecRev} = \sum_t dt \cdot p_{\text{el},t} \cdot E_{\text{prod},t} \quad (7)
$$

总发电量的一部分有资格获得所谓的绿色电力证书， 这些证书可以出售以产生额外收入。然而，预计电力证 书价格在近期将大幅下降，因此在基准情况下忽略了此 项收入。附录C描述了在假设证书价格较高的替代情景下 电力证书的建模方法。

工厂在给定时间段内的总电力产量，$ E_{\text{prod},t} $，等于所 有涡轮机 $ T $ 的电力输出 $ E_{T,t} $ 之和（方程8）。

$$
E_{\text{prod},t} = \sum_T E_{T,t} \quad (8)
$$

锅炉运行、树皮利用和木质素提取

锅炉的部分负荷运行通过使用边际效率来表示，这些边 际效率被估计在锅炉负荷保持高于模型中设定的最低负 荷限制时有效。虽然锅炉效率在部分负荷条件下通常会 降低，但边际效率（即蒸汽生产变化量除以燃料输入变化量）几乎为常数。然而，使用恒定的锅炉边际效率是基于以下假设：树皮锅炉的最低负荷已设定为其在全部运行条件下均具有可接受的效率。

树皮利用 $ Q_{\text{Bark},t} $ 因此由树皮锅炉中的蒸汽产量 $ M^{\text{prod}} {\text{BB},t} $、边际锅炉效率 $ \eta {\text{BB}} $ 以及高压蒸汽和给水的焓 $ h_1 $ 与 $ h_{\text{fw}} $ 决定（公式9）。（蒸汽母管从最高压力开始编号 为 $ j= 1, 2, … $。）木质素提取减少了回收锅炉中的蒸汽生产 $ M^{\text{prod}} {\text{RB},t} $，使其低于参考蒸汽产量 $ M^{\text{ref}} {\text{RB},t} $，该参考 蒸汽产量在不同时间段也有所变化，主要由于燃料锅炉的 黑液流量和热值的变化所致。因此，木质素提取 $ Q_{\text{Lig},t} $ 是 蒸汽产量减少量、锅炉焓增以及回收锅炉的边际木质素效 率 $ \eta_{\text{RB}-\text{LIG}} $ 的函数（公式10）。假设木质素提取装置的 部分负荷效率影响可忽略不计。

$$
Q_{\text{Bark},t} = (h_1 - h_{\text{FW}}) M^{\text{prod}} {\text{BB},t} / \eta {\text{BB}} \quad (9)
$$

$$
Q_{\text{Lig},t} = (h_1 - h_{\text{FW}})(M^{\text{ref}} {\text{RB},t} - M^{\text{prod}} {\text{RB},t}) / \eta_{\text{RB}-\text{LIG}} \quad (10)
$$

之前的模型版本允许根据蒸汽需求启动或停止树皮 锅炉。然而，根据工厂人员的说法，出于安全原因，树 皮锅炉必须始终处于运行状态。因此，回收锅炉和树皮 锅炉必须始终在最小和最大负荷限制范围内运行，此处 由最小和最大蒸汽产量 $ M^{\text{min}}_b $ 和 $ M^{\text{max}}_b $ 定义（公式11）。

$$
M^{\text{min}} {b,t} \leq M^{\text{prod}} {b,t} \leq M^{\text{max}}_{b,t} \quad (11)
$$

此外，$ Q_{\text{Lig},t} $ 的木质素提取还受到黑液可用热含量的 限制，该可用热含量与回收锅炉中的参考蒸汽产量成正 比。因此，最大木质素提取可表示为 $ \rho M^{\text{ref}} {\text{RB},t} $，其中 $ \rho $ 是一个常数参数（公式12）。木质素提取还受到木质素提取 装置投资容量 $ Y {\text{LIG}} $ 的限制（公式13）。

$$
0 \leq Q_{\text{Lig},t} \leq \rho M^{\text{ref}}_{\text{RB},t} \quad (12)
$$

$$
Q_{\text{Lig},t} \leq Y_{\text{LIG}} \quad (13)
$$

汽轮机模型

汽轮机模型是线性函数，用于关联汽轮机 $ T $ 在时间段 $ t $ 内的功率输出 $ E_{T,t} $ 与蒸汽流经涡轮机级 $ s $ 的流量（方程14）。功率输出还与汽轮机 的最大入口蒸汽流量有关。对于现有汽轮机，该最大入口 流量 $ M^{\text{max}} T $ 具有已知值，因此可将其纳入一个通用常数 $ b {T,0}(M^{\text{max}}_T) $ 中。然而，对于新涡轮机，最大入口流量是一个 待优化的变量，$ M^{\text{cap}}_T $。

$$
E_{T,t} = \sum_s a_{T,s} M^{\text{turb}} {T,s,t} +
\begin{cases}
b {T,0} \gamma_T & \text{if } T \text{ existing turbine} \
b_{T,2} M^{\text{cap}} T + b {T,1} & \text{else}
\end{cases} \quad (14)
$$

附录A中描述的参数 $ a_{T,s} $、$ b_{T,0} $、$ b_{T,1} $ 和 $ b_{T,2} $ 的估计方法，附录A还讨论了现有汽轮机的汽轮机模型验证。

在与工厂员工讨论后，认为允许汽轮机在不同时间 段内投入和停止运行是不现实的。然而，应考虑用新的、 更高效的汽轮机替换现有汽轮机的机会。因此，模型中 包含了一个变量 $ \gamma_T $，用于表示永久关闭现有汽轮机的选 择。如果对新涡轮机容量进行投资，则假设这些新涡轮 机始终处于运行状态。如果保留现有汽轮机继续运行， 则二元变量 $ \gamma_T $ 取值为1。此时方程(15)确保入口蒸汽流量 保持在最小和最大流量限制之间，其中参数 $ \mu^{\text{min}}_T $ 将汽轮 机的最小入口流量定义为最大入口流量的一个分数。对 于新涡轮机，相应的约束由方程(16)给出。相反，如果某 台现有汽轮机停止运行，则变量 $ \gamma_T $ 取值为0，根据方程 (15)将其入口蒸汽流量设为零，从而该汽轮机的功率输出 也为零，如方程(14)所示。

$$
\mu^{\text{min}} T \gamma_T M^{\text{max}}_T \leq M^{\text{turb}} {T,1,t} \leq \gamma_T M^{\text{max}}_T \quad \text{for existing turbines } T \quad (15)
$$

$$
\mu^{\text{min}} T M^{\text{cap}}_T \leq M^{\text{turb}} {T,1,t} \leq M^{\text{cap}}_T \quad \text{for new turbines } T \quad (16)
$$

最后，添加了一些约束以表示汽轮机的最大抽汽流量 和最大功率输出。在汽轮机 $ T $ 的涡轮级 $ s(T) $ 之后的抽汽 流量 $ M^{\text{ext}} {T,s,t} $ 由方程(17)给出。对于现有汽轮机，抽汽量受 最大抽汽流量 $ M^{\text{max ext}} {T,s} $ 的限制，如方程(18)所示。针对新 涡轮机的最大抽汽流量的相应约束未被包含。由于最大抽 汽流量应取决于安装的涡轮机容量的大小，因此不能将其 设为固定参数。然而，在增加其值不产生任何成本的情况 下，将其作为变量引入并无意义。因此，对于新涡轮机， 采用最大功率输出，$ E_{T,t} $ 受设计容量 $ E^{\text{max}}_T $ （方程19）的限制，而该设计容量又 用于确定投资成本函数中使用的汽轮机容量，详见下文。

$$
M^{\text{ext}} {T,s,t} =
\begin{cases}
M^{\text{turb}} {T,s,t} & \text{if } s(T) \text{ last turbine stage} \
M^{\text{turb}} {T,s,t} - M^{\text{turb}} {T,s+1,t} & \text{else}
\end{cases} \quad (17)
$$

$$
M^{\text{ext}} {T,s,t} \leq M^{\text{max ext}} {T,s} \quad \text{for existing turbines } T \quad (18)
$$

$$
E_{T,t} \leq E^{\text{max}}_T \quad \text{for new turbines } T \quad (19)
$$

为了使汽轮机模型的线性表达式（方程14）在固定 系数下成立，汽轮机T应为背压抽汽式汽轮机或低压凝汽 式汽轮机。原则上，可以考虑多种不同的背压式与凝汽 式汽轮机组合，其入口和抽汽连接至不同的集管。尽管 上述汽轮机约束是通用的，但仍需要一些更具体的约束 来描述工厂中特定新涡轮机的投资机会。在该案例研究 中，考虑了新涡轮机投资的三个主要替代方案，即：
– TURB1：一台背压抽汽式汽轮机（BPETa），在27、 12和4巴（绝）联箱处有抽汽。
– TURB2：一台低压凝 汽式汽轮机（LPCTa）。
– TURB3：一台组合式汽轮 机，进口接高压蒸汽联箱（1号联箱），在27、12和4巴 （绝）联箱处有抽汽，并带有凝汽尾部。该汽轮机建模 为三级背压抽汽式汽轮机（BPETb）与低压凝汽式汽轮 机（LPCTb）的组合。

增加了额外的约束（方程20–22），以将单个涡轮机的 最大功率输出与投资成本函数中使用的汽轮机容量关联 起来。在实际应用中，TURB3根据上述方程(14–19)被建 模为两个独立的涡轮机，并添加一个约束条件，即凝汽 级的入口流量必须小于或等于汽轮机高压段末级的出口 流量（方程23）。

$$
E^{\text{max}} {\text{BPETa}} \leq Y {\text{TURB1}} \quad (20)
$$

$$
E^{\text{max}} {\text{LPCTa}} \leq Y {\text{TURB2}} \quad (21)
$$

$$
E^{\text{max}} {\text{BPETb}} + E^{\text{max}} {\text{LPCTb}} \leq Y_{\text{TURB3}} \quad (22)
$$

$$
M^{\text{turb}} {\text{LPCTb},1,t} \leq M^{\text{turb}} {\text{BPETb},3,t} \quad (23)
$$

质量与能量平衡

蒸汽联箱数据被假定为常数，且不被模型优化。蒸汽母管按编 号排列 $ j= 1, 2, … $，从最高压力开始。蒸汽压力母管 $ j $ 的质量 平衡在公式(24)–(26)中表述。$ M^{\text{turb}} {T,s,t} $、$ M^{\text{vlv}} {v,t} $ 和 $ M^{\text{vent}} t $ 分别 表示通过涡轮机级 $ s(T) $、膨胀阀 $ v $ 和排向大气的放空蒸汽 的蒸汽流量；符号 $ \text{in}() $ 和 $ \text{out}() $ 指的是涡轮机、涡轮机级 和阀门的入口和出口集管，视具体情况而定，用于标记涡 轮机、涡轮机级和阀门的子集，这些子集的蒸汽流量应包 含在某一特定集管的质量平衡中。$ M^{\text{proc}} {j,t} $ 表示工艺蒸汽 需求，$ M^{\text{qwj},t} $ 表示为饱和目的添加到蒸汽母管 $ j $ 的淬冷水。

如公式(24–25)所述的质量平衡并非针对特定工厂， 但仍未完全通用。具体而言，假设涡轮机仅在最高压力 蒸汽母管或最低压力蒸汽母管处有入口，且大气排放口 仅位于最低压力母管处。然而，该质量平衡可用于表示 任意数量的蒸汽母管、阀门和涡轮机，且阀门的进出口 以及涡轮机的出口可位于任一母管。

工艺蒸汽需求 $ M^{\text{proc}} {j,t} $ 根据方程(26)计算得出。基准 蒸汽需求 $ M^{\text{proc, ref}} {j,t} $ 表示在未实施木质素提取或新增凝汽 式汽轮机的情况下工厂的蒸汽需求，即不受模型所优化的 蒸汽公用系统投资或运行变化影响的参考需求。对于产量 增加情景，该基准蒸汽需求由预计的未来工艺蒸汽需求给 出。如果进行木质素提取，则木质素提取过程中使用的洗 涤水将返回蒸发站，导致需要额外的蒸汽以蒸发增加的水 量。因此，在模型中，当提取木质素时，会在基准蒸汽需 求基础上增加一个低压蒸汽需求，该需求取决于木质素提 取率 $ Q_{\text{Lig},t} $ 以及每兆瓦木质素
黑液处理量以及对4和12巴（绝对）蒸汽的需求（这两者 平均将增加约80%）。此外，计划更改目前使用高压蒸 汽（61巴（绝对））进行吹灰的方式，改用27巴（绝对） 蒸汽。当纸浆产量增加导致黑液热流上升时，现有的回 收锅炉将成为瓶颈。然而，工厂内仍有一台目前未运行 的旧回收锅炉，计划在产量增加的同时重新启用。但即 便如此，两台回收锅炉共同运行仍不足以应对产量增加 后高负荷生产期间的全部黑液流量。因此，计划建设一 套木质素提取装置作为解瓶颈方案。

本研究中，采用优化模型确定木质素提取装置的最 优容量，以及在黑液热能可用性和工艺蒸汽需求预设变 化情况下新汽轮机容量的最佳投资。假设纸浆产量增加 是给定的，且不受木质素提取率变化的影响（只要提取 率不低于解除回收锅炉瓶颈所需水平）。当增加木质素 提取使得回收锅炉不再成为瓶颈时，若蒸煮器、蒸发或 漂白装置等其他工艺环节也存在进一步增产的容量限制， 则该假设是合理的。此外，假设若需消除蒸汽主管道的 瓶颈，相关改造已包含在给定的纸浆生产投资计划中， 无需进一步优化。

优化模型

本研究中使用的优化模型是一个多周期混合整数线性规 划（MILP）模型。该MILP模型用于确定最优设计决策 （在木质素提取和/或新涡轮机方面的投资容量），同时 考虑在给定投资以及价格和工艺蒸汽需求变化的情况下， 蒸汽生产和汽轮机运行的最优响应。

以下章节所述的优化模型是在先前应用于工厂示例 建模的模型基础上开发的（斯文森 2014，2015）。然而， 将该优化模型应用于实际工厂时，发现需要对模型的某 些部分进行调整。这些调整旨在考虑额外的运行约束， 以及处理设备性能数据的缺失或不确定性问题，以便根据实测数据对模型进行调优。此外，经过与工厂 员工讨论后，模型排除了每日启停锅炉或汽轮机的可能 性，因为工厂员工认为，为了实现运行优化而频繁启动 和关闭锅炉、汽轮机以及木质素提取设备在技术和经济 上均不可行。

优化的目标是：
最小化 $ r \times \text{投资成本} + \text{树皮燃料成本} - \text{木质素提取收入} - \text{电力生产收入} $ (1)

其中，总投资成本InvCost通过资本回收系数r进行年金化， BarkCost表示树皮的年燃料成本，LigRev表示木质素提 取的年运行收入，ElecRev表示电力生产的年收入。该目 标通过优化投资、树皮锅炉的蒸汽产量、木质素提取率 以及通过汽轮机的蒸汽流量来实现。

投资成本

总投资成本 InvCost 可能包括对新涡轮机和木质素提取装 置的投资（公式2）。设备 $ x $ 的投资成本函数 $ Cost_x(Y_x) $ 通过分段线性函数（在 $ n $ 个线性化区间内）表示为设备 容量 $ Y_x $ 的函数（公式3）。$ C_{\text{inv},x}(i) $ 表示分段线性函数第 $ i $th 个断点处的投资成本，$ Y_x(i) $ 表示该断点处的设备容量， $ k_x(i) $ 表示 $ Y_x(i) $ 和 $ Y_x(i+ 1) $ 之间的线性斜率。二元变量 $ z_x $ 在对技术 $ x $ 进行投资时为1，否则为0。如果对技术 $ x $ 进行投资，则设备容量 $ Y_x $ 必须位于投资成本函数的有效 线性化范围内，即在第一个线性化区间的起点 $ Y_x(1) $ 和最 后一个区间的终点 $ Y_x(n + 1) $ 之间。这由公式(4)给出。

$$
\text{InvCost} = \sum_x \text{Cost}_x(Y_x) \quad (2)
$$

$$
\text{Cost} x(Y_x) =
\begin{cases}
0, & Y_x = 0 \
C {\text{inv},x}(i) + k_x(i)(Y_x - Y_x(i)), & Y_x(i) \leq Y_x < Y_x(i+1), i
\end{cases} \quad (3)
$$

$$
z_x Y_x(1) \leq Y_x \leq z_x Y_x(n+1) \quad (4)
$$

运行成本和收入

年被划分为时间段 $ t $，其持续时间为 $ dt $，代表工厂的总年 运行时间。

BarkCost 是树皮价格 $ p_{\text{bark},t} $ 以及树皮在树皮锅炉中 作为燃料的使用量 $ Q_{\text{Bark},t} $ 的年树皮成本函数，这两者在 不同时间段 $ t $ 内可能变化（公式5）。类似地，与木质素 提取 $ Q_{\text{Lig},t} $ 相关的年木质素收入 $ \text{LigRev} $ 是不同时间段内 木质素价格 $ p_{\text{lig},t} $ 的函数（公式6）。

$$
\text{BarkCost} = \sum_t dt \cdot p_{\text{bark},t} \cdot Q_{\text{Bark},t} \quad (5)
$$

$$
\text{LigRev} = \sum_t dt \cdot p_{\text{lig},t} \cdot Q_{\text{Lig},t} \quad (6)
$$

电力生产收入表示来自电力生产的年度收入，$ E_{\text{prod},t} $（公式7）。在蒸汽轮机中生产的电力，$ E_{\text{prod},t} $，可被工 厂自用，从而减少从电网购电，或售电给电网。由于锅炉 和汽轮机负荷变化引起的自用电量变化，例如空气风机和 蒸汽冷凝泵的影响，已被忽略。假设购电和售电采用相同 的电价 $ p_{\text{el},t} $。如果工厂的电力消耗数据具有与模型相同的 时间分辨率，则可通过增加一个工厂电力平衡的约束条件， 轻松调整模型以适应不同的购电/售电价格。

$$
\text{ElecRev} = \sum_t dt \cdot p_{\text{el},t} \cdot E_{\text{prod},t} \quad (7)
$$

总发电量的一部分有资格获得所谓的绿色电力证书， 这些证书可以出售以产生额外收入。然而，预计电力证 书价格在近期将大幅下降，因此在基准情况下忽略了此 项收入。附录C描述了在假设证书价格较高的替代情景下 电力证书的建模方法。

工厂在给定时间段内的总电力产量，$ E_{\text{prod},t} $，等于所 有涡轮机 $ T $ 的电力输出 $ E_{T,t} $ 之和（方程8）。

$$
E_{\text{prod},t} = \sum_T E_{T,t} \quad (8)
$$

锅炉运行、树皮利用和木质素提取

锅炉的部分负荷运行通过使用边际效率来表示，这些边 际效率被估计在锅炉负荷保持高于模型中设定的最低负 荷限制时有效。虽然锅炉效率在部分负荷条件下通常会 降低，但边际效率（即蒸汽生产变化量除以燃料输入变化量）几乎为常数。然而，使用恒定的锅炉边际效率是基于以下假设：树皮锅炉的最低负荷已设定为其在全部运行条件下均具有可接受的效率。

树皮利用 $ Q_{\text{Bark},t} $ 因此由树皮锅炉中的蒸汽产量 $ M^{\text{prod}} {\text{BB},t} $、边际锅炉效率 $ \eta {\text{BB}} $ 以及高压蒸汽和给水的焓 $ h_1 $ 与 $ h_{\text{fw}} $ 决定（公式9）。（蒸汽母管从最高压力开始编号 为 $ j= 1, 2, … $。）木质素提取减少了回收锅炉中的蒸汽生产 $ M^{\text{prod}} {\text{RB},t} $，使其低于参考蒸汽产量 $ M^{\text{ref}} {\text{RB},t} $，该参考 蒸汽产量在不同时间段也有所变化，主要由于燃料锅炉的 黑液流量和热值的变化所致。因此，木质素提取 $ Q_{\text{Lig},t} $ 是 蒸汽产量减少量、锅炉焓增以及回收锅炉的边际木质素效 率 $ \eta_{\text{RB}-\text{LIG}} $ 的函数（公式10）。假设木质素提取装置的 部分负荷效率影响可忽略不计。

$$
Q_{\text{Bark},t} = (h_1 - h_{\text{FW}}) M^{\text{prod}} {\text{BB},t} / \eta {\text{BB}} \quad (9)
$$

$$
Q_{\text{Lig},t} = (h_1 - h_{\text{FW}})(M^{\text{ref}} {\text{RB},t} - M^{\text{prod}} {\text{RB},t}) / \eta_{\text{RB}-\text{LIG}} \quad (10)
$$

之前的模型版本允许根据蒸汽需求启动或停止树皮 锅炉。然而，根据工厂人员的说法，出于安全原因，树 皮锅炉必须始终处于运行状态。因此，回收锅炉和树皮 锅炉必须始终在最小和最大负荷限制范围内运行，此处 由最小和最大蒸汽产量 $ M^{\text{min}}_b $ 和 $ M^{\text{max}}_b $ 定义（公式11）。

$$
M^{\text{min}} {b,t} \leq M^{\text{prod}} {b,t} \leq M^{\text{max}}_{b,t} \quad (11)
$$

此外，$ Q_{\text{Lig},t} $ 的木质素提取还受到黑液可用热含量的 限制，该可用热含量与回收锅炉中的参考蒸汽产量成正 比。因此，最大木质素提取可表示为 $ \rho M^{\text{ref}} {\text{RB},t} $，其中 $ \rho $ 是一个常数参数（公式12）。木质素提取还受到木质素提取 装置投资容量 $ Y {\text{LIG}} $ 的限制（公式13）。

$$
0 \leq Q_{\text{Lig},t} \leq \rho M^{\text{ref}}_{\text{RB},t} \quad (12)
$$

$$
Q_{\text{Lig},t} \leq Y_{\text{LIG}} \quad (13)
$$

汽轮机模型

汽轮机模型是线性函数，用于关联汽轮机 $ T $ 在时间段 $ t $ 内的功率输出 $ E_{T,t} $ 与蒸汽流经涡轮机级 $ s $ 的流量（方程14）。功率输出还与汽轮机 的最大入口蒸汽流量有关。对于现有汽轮机，该最大入口 流量 $ M^{\text{max}} T $ 具有已知值，因此可将其纳入一个通用常数 $ b {T,0}(M^{\text{max}}_T) $ 中。然而，对于新涡轮机，最大入口流量是一个 待优化的变量，$ M^{\text{cap}}_T $。

$$
E_{T,t} = \sum_s a_{T,s} M^{\text{turb}} {T,s,t} +
\begin{cases}
b {T,0} \gamma_T & \text{if } T \text{ existing turbine} \
b_{T,2} M^{\text{cap}} T + b {T,1} & \text{else}
\end{cases} \quad (14)
$$

附录A中描述的参数 $ a_{T,s} $、$ b_{T,0} $、$ b_{T,1} $ 和 $ b_{T,2} $ 的估计方法，附录A还讨论了现有汽轮机的汽轮机模型验证。

在与工厂员工讨论后，认为允许汽轮机在不同时间 段内投入和停止运行是不现实的。然而，应考虑用新的、 更高效的汽轮机替换现有汽轮机的机会。因此，模型中 包含了一个变量 $ \gamma_T $，用于表示永久关闭现有汽轮机的选 择。如果对新涡轮机容量进行投资，则假设这些新涡轮 机始终处于运行状态。如果保留现有汽轮机继续运行， 则二元变量 $ \gamma_T $ 取值为1。此时方程(15)确保入口蒸汽流量 保持在最小和最大流量限制之间，其中参数 $ \mu^{\text{min}}_T $ 将汽轮 机的最小入口流量定义为最大入口流量的一个分数。对 于新涡轮机，相应的约束由方程(16)给出。相反，如果某 台现有汽轮机停止运行，则变量 $ \gamma_T $ 取值为0，根据方程 (15)将其入口蒸汽流量设为零，从而该汽轮机的功率输出 也为零，如方程(14)所示。

$$
\mu^{\text{min}} T \gamma_T M^{\text{max}}_T \leq M^{\text{turb}} {T,1,t} \leq \gamma_T M^{\text{max}}_T \quad \text{for existing turbines } T \quad (15)
$$

$$
\mu^{\text{min}} T M^{\text{cap}}_T \leq M^{\text{turb}} {T,1,t} \leq M^{\text{cap}}_T \quad \text{for new turbines } T \quad (16)
$$

最后，添加了一些约束以表示汽轮机的最大抽汽流量 和最大功率输出。在汽轮机 $ T $ 的涡轮级 $ s(T) $ 之后的抽汽 流量 $ M^{\text{ext}} {T,s,t} $ 由方程(17)给出。对于现有汽轮机，抽汽量受 最大抽汽流量 $ M^{\text{max ext}} {T,s} $ 的限制，如方程(18)所示。针对新 涡轮机的最大抽汽流量的相应约束未被包含。由于最大抽 汽流量应取决于安装的涡轮机容量的大小，因此不能将其 设为固定参数。然而，在增加其值不产生任何成本的情况 下，将其作为变量引入并无意义。因此，对于新涡轮机， 采用最大功率输出，$ E_{T,t} $ 受设计容量 $ E^{\text{max}}_T $ （方程19）的限制，而该设计容量又 用于确定投资成本函数中使用的汽轮机容量，详见下文。

$$
M^{\text{ext}} {T,s,t} =
\begin{cases}
M^{\text{turb}} {T,s,t} & \text{if } s(T) \text{ last turbine stage} \
M^{\text{turb}} {T,s,t} - M^{\text{turb}} {T,s+1,t} & \text{else}
\end{cases} \quad (17)
$$

$$
M^{\text{ext}} {T,s,t} \leq M^{\text{max ext}} {T,s} \quad \text{for existing turbines } T \quad (18)
$$

$$
E_{T,t} \leq E^{\text{max}}_T \quad \text{for new turbines } T \quad (19)
$$

为了使汽轮机模型的线性表达式（方程14）在固定 系数下成立，汽轮机T应为背压抽汽式汽轮机或低压凝汽 式汽轮机。原则上，可以考虑多种不同的背压式与凝汽 式汽轮机组合，其入口和抽汽连接至不同的集管。尽管 上述汽轮机约束是通用的，但仍需要一些更具体的约束 来描述工厂中特定新涡轮机的投资机会。在该案例研究 中，考虑了新涡轮机投资的三个主要替代方案，即：
– TURB1：一台背压抽汽式汽轮机（BPETa），在27、 12和4巴（绝）联箱处有抽汽。
– TURB2：一台低压凝 汽式汽轮机（LPCTa）。
– TURB3：一台组合式汽轮 机，进口接高压蒸汽联箱（1号联箱），在27、12和4巴 （绝）联箱处有抽汽，并带有凝汽尾部。该汽轮机建模 为三级背压抽汽式汽轮机（BPETb）与低压凝汽式汽轮 机（LPCTb）的组合。

增加了额外的约束（方程20–22），以将单个涡轮机的 最大功率输出与投资成本函数中使用的汽轮机容量关联 起来。在实际应用中，TURB3根据上述方程(14–19)被建 模为两个独立的涡轮机，并添加一个约束条件，即凝汽 级的入口流量必须小于或等于汽轮机高压段末级的出口 流量（方程23）。

$$
E^{\text{max}} {\text{BPETa}} \leq Y {\text{TURB1}} \quad (20)
$$

$$
E^{\text{max}} {\text{LPCTa}} \leq Y {\text{TURB2}} \quad (21)
$$

$$
E^{\text{max}} {\text{BPETb}} + E^{\text{max}} {\text{LPCTb}} \leq Y_{\text{TURB3}} \quad (22)
$$

$$
M^{\text{turb}} {\text{LPCTb},1,t} \leq M^{\text{turb}} {\text{BPETb},3,t} \quad (23)
$$

质量与能量平衡

蒸汽联箱数据被假定为常数，且不被模型优化。蒸汽母管按编 号排列 $ j= 1, 2, … $，从最高压力开始。蒸汽压力母管 $ j $ 的质量 平衡在公式(24)–(26)中表述。$ M^{\text{turb}} {T,s,t} $、$ M^{\text{vlv}} {v,t} $ 和 $ M^{\text{vent}} t $ 分别 表示通过涡轮机级 $ s(T) $、膨胀阀 $ v $ 和排向大气的放空蒸汽 的蒸汽流量；符号 $ \text{in}() $ 和 $ \text{out}() $ 指的是涡轮机、涡轮机级 和阀门的入口和出口集管，视具体情况而定，用于标记涡 轮机、涡轮机级和阀门的子集，这些子集的蒸汽流量应包 含在某一特定集管的质量平衡中。$ M^{\text{proc}} {j,t} $ 表示工艺蒸汽 需求，$ M^{\text{qwj},t} $ 表示为饱和目的添加到蒸汽母管 $ j $ 的淬冷水。

如公式(24–25)所述的质量平衡并非针对特定工厂， 但仍未完全通用。具体而言，假设涡轮机仅在最高压力 蒸汽母管或最低压力蒸汽母管处有入口，且大气排放口 仅位于最低压力母管处。然而，该质量平衡可用于表示 任意数量的蒸汽母管、阀门和涡轮机，且阀门的进出口 以及涡轮机的出口可位于任一母管。

工艺蒸汽需求 $ M^{\text{proc}} {j,t} $ 根据方程(26)计算得出。基准 蒸汽需求 $ M^{\text{proc, ref}} {j,t} $ 表示在未实施木质素提取或新增凝汽 式汽轮机的情况下工厂的蒸汽需求，即不受模型所优化的 蒸汽公用系统投资或运行变化影响的参考需求。对于产量 增加情景，该基准蒸汽需求由预计的未来工艺蒸汽需求给 出。如果进行木质素提取，则木质素提取过程中使用的洗 涤水将返回蒸发站，导致需要额外的蒸汽以蒸发增加的水 量。因此，在模型中，当提取木质素时，会在基准蒸汽需 求基础上增加一个低压蒸汽需求，该需求取决于木质素提 取率 $ Q_{\text{Lig},t} $ 以及每兆瓦木质素提取导致的低压蒸汽流量比 增加值 $ \sigma $。由于此蒸汽需求增加而导致的冷凝液流量向给 水系统的潜在影响被忽略。然而，如果通过凝汽式涡轮机 的蒸汽流量 $ M^{\text{turb}} {T,s,t} $ 相较于基准汽轮机冷凝液流量 $ M^{\text{ref cond}}_t $ 有 所增加，则冷凝水加热所需的蒸汽需求也会相应增加。焓 $ h {\text{fw}} $、$ h_{\text{cw}} $、$ h_j $ 分别指给水、冷凝水和在集管j处蒸汽的焓。

$$
M^{\text{prod}} {\text{RB},t} + M^{\text{prod}} {\text{BB},t} = M^{\text{proc}} {1,t} + \sum {T:\text{in}(T) = 1} M^{\text{turb}} {T,1,t} + \sum {v:\text{in}(v) = 1} M^{\text{vlv}}_{v,t} \quad (24)
$$

$$
\sum_{T,s(T):\text{out}(s) = j} M^{\text{ext}} {T,s,t} + \sum {v:\text{out}(v) = j} M^{\text{vlv}} {v,t} + M^{\text{qw}} {j,t} =
\begin{cases}
M^{\text{proc}} {j,t} + \sum {v:\text{in}(v) = j} M^{\text{vlv}} {v,t} & j = 2, …, j {\text{max}} - 1 \
\sum_{T:\text{in}(T) = j} M^{\text{turb}} {T,s,t} + M^{\text{vent}}_t & j = j {\text{max}}
\end{cases} \quad (25)
$$

$$
M^{\text{proc}} {j,t} =
\begin{cases}
M^{\text{proc, ref}} {j,t} & \text{if } j < j_{\text{max}} \
\sigma Q_{\text{Lig},t} + \left( \sum_{T,s(T):\text{out}(s) = \text{cw}} M^{\text{turb}} {T,s,t} - M^{\text{ref cond}}_t \right) \frac{h {\text{fw}} - h_{\text{cw}}}{h_6 - h_{\text{fw}}} & \text{else}
\end{cases} \quad (26)
$$

某些工艺蒸汽需求（例如用于给水预热的蒸汽）会 随锅炉负荷而变化。该锅炉负荷依赖性在模型中被忽略 （有关此简化的讨论，请参见模型简化与发展需求部分）。

蒸汽母管的能量平衡由公式(27)给出，其中 $ h^{\text{ext}}_{T,s} $ 表 示从涡轮级抽汽流量的估算焓值。实际上，该值会随着 通过涡轮级的蒸汽流量而变化，但为了保持模型的线性， 采用了一个恒定的估算值。

$$
\sum_{v:\text{out}(v) = j} M^{\text{vlv}} {v,t} h {\text{in}(v)} + \sum_{T,s(T):\text{out}(s) = j} M^{\text{ext}} {T,s,t} h^{\text{ext}} {T,s} + M^{\text{qw}} {j,t} h {\text{qw}} = \left( \sum_{v:\text{out}(v) = j} M^{\text{vlv}} {v,t} + \sum {T,s(T):\text{out}(s) = j} M^{\text{ext}} {T,s,t} + M^{\text{qw}} {j,t} \right) h_j \quad j > 1 \quad (27)
$$