利用复morlet小波变换实现信号的包络提取（matlab）——学习笔记1

**

利用复morlet小波变换实现信号的包络提取（matlab）——学习笔记1

---

小波变换概念

在复morlet小波变换中，母小波（小波基函数），是一个高斯包络下的单频率复正弦函数，其中复三角函数与频率相对应，而呈指数衰减的高斯函数对应于函数时域的有限支撑。小波基函数公式如下：
$$\varphi (z)=\exp (-t^2/2)\ast exp(j{w}_{0}t)$$
对小波基函数进行伸缩平移：
$${\varphi }_{a,b}(z)=1/\sqrt{a}\ast exp[-(t-b{)}^2/2a^2]\ast exp[j{w}_0(t-b)/a]$$
其中，a为尺度因子，通过改变a的大小（尺度变换），对小波函数进行伸缩。尺度因子a越大，函数中心频率越低（看复三角函数），函数指数衰减越慢，时域支撑区间越大（看高斯函数），则频域带宽越小，频域的分辨率越高，a越小时，变化则相反。时移因子b则实现小波函数在坐标轴上的平移。

clc
clear
close all;
w0=10;
z0=5;
a=1;
z=linspace(0,10,1000);
wav1=exp((-1*((z-z0)./a).^2)/2);
wav2=cos(w0*(z-z0)./a)+i*sin(w0*(z-z0)./a);
wav=wav1.*wav2;
wavr=real(wav);
figure,plot(z,wavr,'linewidth',3),xlabel('z'),title('小波实部'),set(gcf,'color','w');

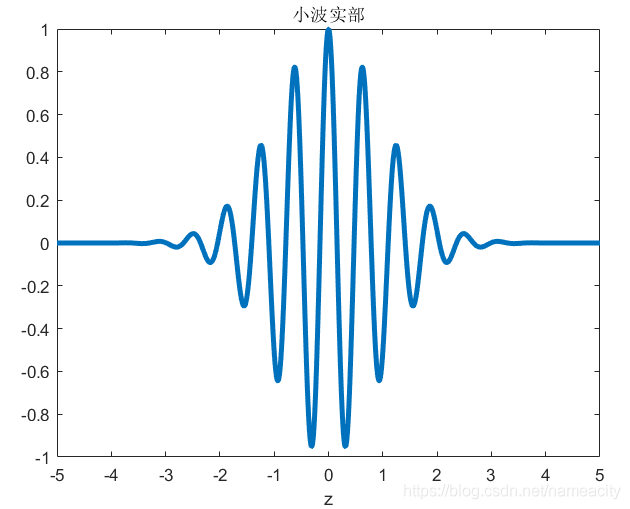
中心频率为10，尺度因子a取1，时移因子b取0

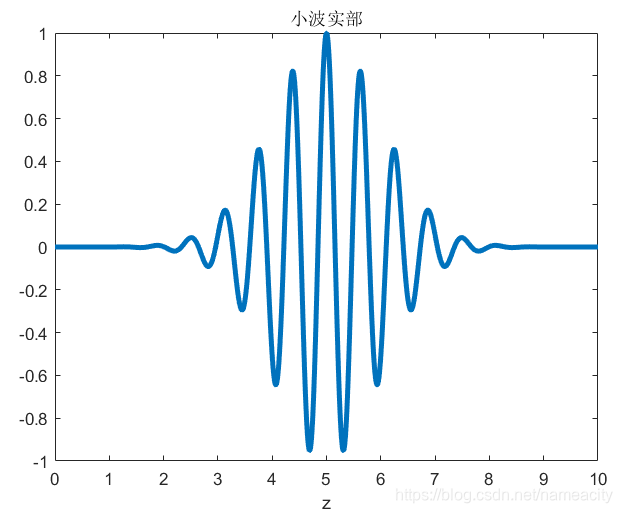
中心频率为10，尺度因子a取1，时移因子b取5

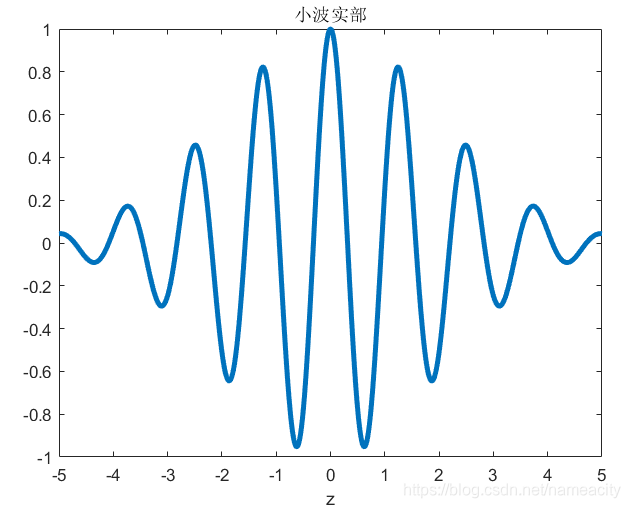
中心频率为10，尺度因子a取2，时移因子b取0

小波变换的公式如下：
$$WT(a,b)={\int }_{-\infty }^{\infty }f(z)\ast {\varphi }_{a,b}^{\ast }[(z-b)/a]dz$$
则小波系数为：
$$|WT(a,b)|=\sqrt{W{T}_r(a,b{)}^2+W{T}_i(a,b{)}^2}$$
即原始信号f与小波函数乘积再积分的过程，类似于卷积过程，其得到的小波系数实际上表示原始信号与小波函数的相关性大小，相关性越大，小波系数越大。

---

小波变换的本质

选取一个小波基函数（与中心频率w0相对应），通过尺度变换得到一系列的中心频率（w0/a），又通过时移得到一系列在不同区间的基函数，再分别和原始信号（对应区间）乘积再积分，产生的极值对应的频率就是原始信号在这一区间的频率。也就是说，小波变换本质上类似于一个带通滤波器，只允许频率和自身中心频率相近的信号通过。下图为某个信号（含两个包络）小波变换图，坐标值的大小对应小波系数的大小，横坐标对应时间（空间），纵坐标为尺度：

coef=cwt(I_signal,scale,wavename,'plot');

---

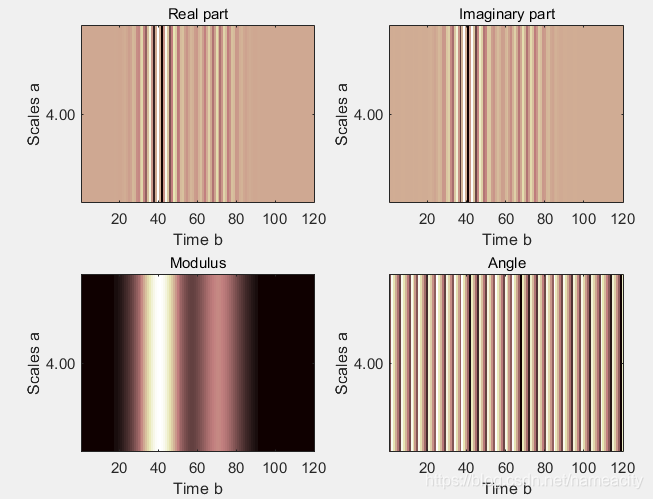
利用小波变换实现包络提取

需要用到的函数与公式

cwt(f,scales,‘wavename’,‘plot’): f为原始信号，scales为尺度大小，wavename为选择的小波基函数
centfrq(‘wavename’): 获取小波中心频率
fa=(fc*fs)/a: fa为尺度对应的实际频率，a为尺度，fs为原始信号的采样频率，fc为小波基函数的中心频率

包络提取

通过原始信号和选择的小波基函数得到实际频率fa，中心频率fc，采样频率fs，即可得到包络提取所需要的尺度大小，进而进行小波变换。
原始信号：

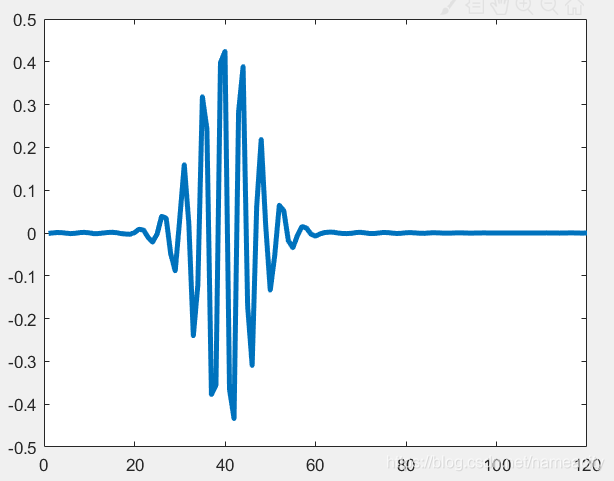
选取复morlet小波（matlab函数形式：cmorfb-fc，fb为带宽参数，fc为中心频率），对其进行包络提取：

coef=cwt(I_signal,scale,wavename);
coef=abs(coef);
plot(scanstep,coef,'r','linewidth',3);

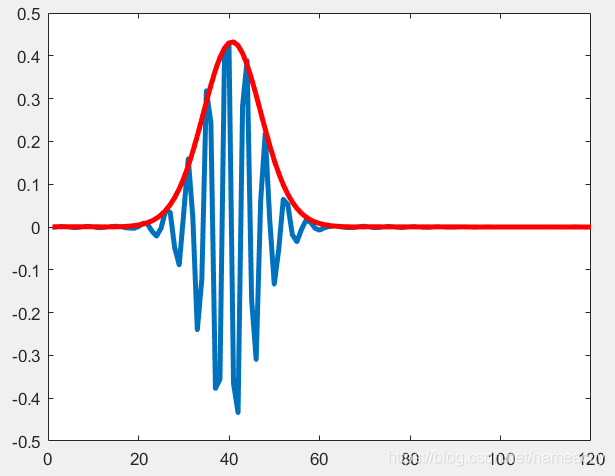
对得到的包络线进行三次样条插值（spline）：

xx=1:0.001:120;
yy=spline(scanstep,coef,xx);   %三次样条插值
figure,plot(xx,yy,'r','linewidth',3);

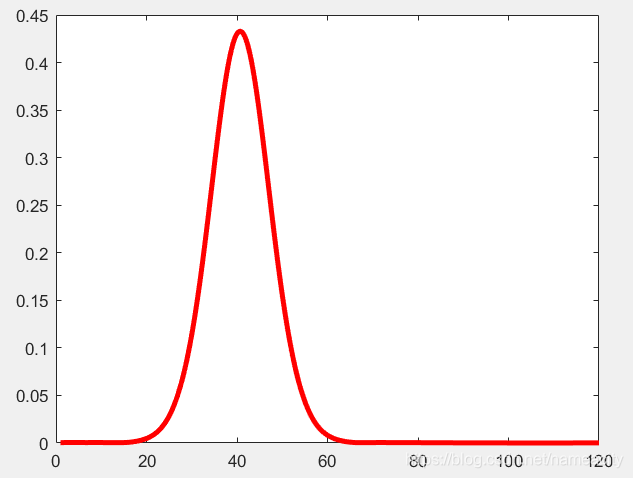
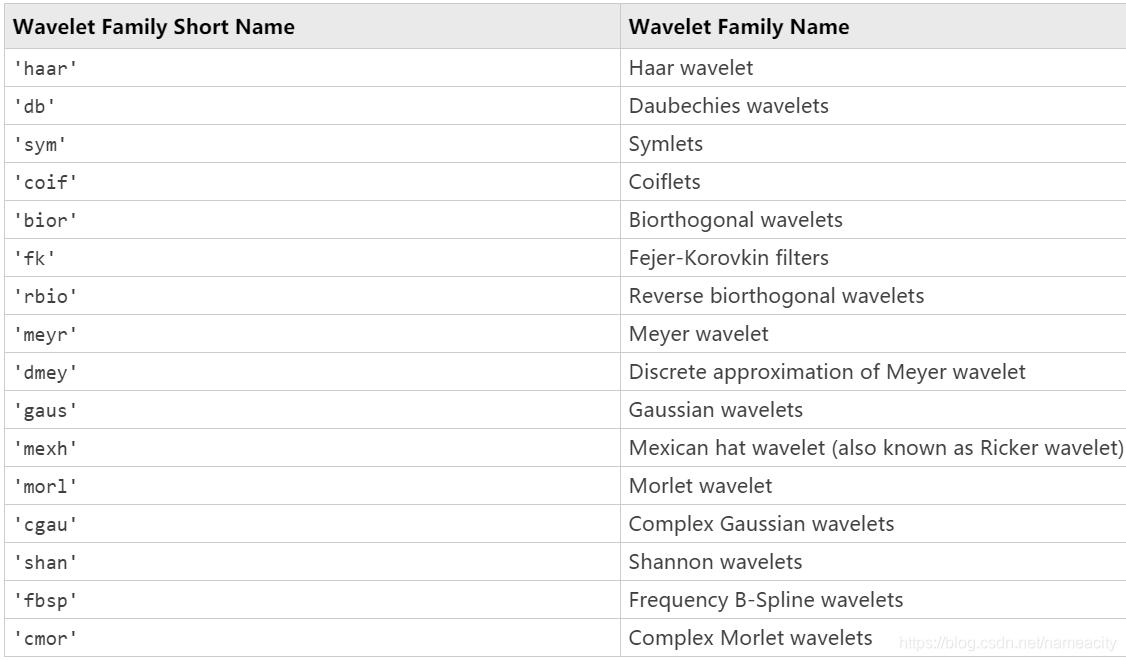
根据原始信号的不同，需要选用不同的小波基函数，改变小波基函数的中心频率fc和带宽fb等参数，进而找到最贴近原始信号的包络。下图为matlab自带的小波函数：