大津法（OTSU）进行阈值分割（matlab一维信号处理）——学习笔记2

大津法（OTSU）进行阈值分割——学习笔记2

OTSU原理

大津法常用于图像的阈值分割，通过搜寻目标与背景之间的最大方差来自适应地确定图像分割的最佳阈值。
对于一个一维干涉信号，首先对信号进行归一化，将信号减去直流部分，然后对信号取绝对值（或平方或四次方），得到类似灰度直方图。假设该信号共有N个数据点，每个数据点值的大小为N（i），则每个数据点值的总和为sum（N），每个数据点占总体的概率为pi=N(i)/sum(N)，将处理后的信号分为A、B两部分，则各部分占总体的概率为：
$$\begin{gathered} w_a=\sum _{i=1}^t{p}_i \\ {w}_b=\sum _{i=t+1}^N{p}_i \end{gathered}$$
A和B中各点所占的概率分别为：
$$\begin{gathered} p_i/w_a(i=1,2,,3,4\dots \dots t), \\ {p}_i/w_b(i=t+1,t+2,\dots \dots N) \end{gathered}$$
信号总体（所有数据点）的数学期望可表示为：
$$E=\sum _{i=1}^N{p}_i\ast i$$
A、B两部分各自的数学期望大小为：
$$u_a=\sum _{i=1}^t{p}_i\ast i/w_a,u_b=\sum _{i=t+1}^N{p}_i\ast i/w_b$$
则该信号的类间方差为：
$${\delta }_1^2=w_a(u_a-E{)}^2+w_b(u_b-E{)}^2$$
j假设A、B相互独立时，其各自的方差为：
$${\delta }_a^2=\sum _{i=1}^t(p_i/w_a)\ast (i-u_a{)}^2,{\delta }_b^2=\sum _{i=t+1}^N(p_i/w_b)\ast (i-u_b{)}^2$$
则该信号的类内方差为：
$${\delta }_2^2=w_a\ast {\delta }_a^2+w_b\ast {\delta }_b^2$$
则理想的分割阈值位于类间方差最大、类内方差最小的位置。

---

信号处理

原始信号（含有两个包络）

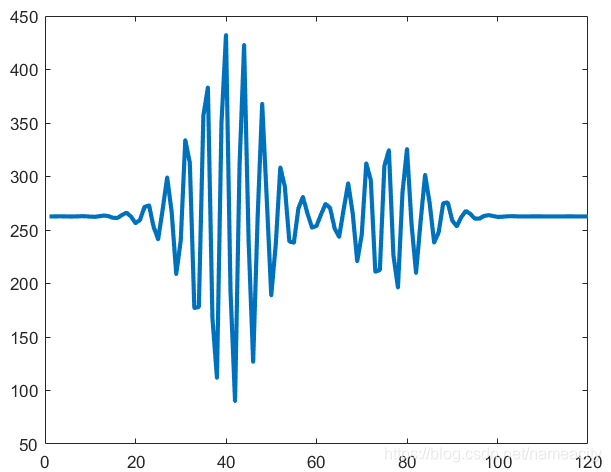
对该信号进行预处理，减去直流项，然后取平方，得到类似直方图的新的信号形式：

I_signal=I_signal-mean(I_signal);                      
I_gray=I_signal.^2;         
figure,plot(scanstep,I_gray,'linewidth',2.5),title('将原始信号处理成类似灰度直方图形式');

---

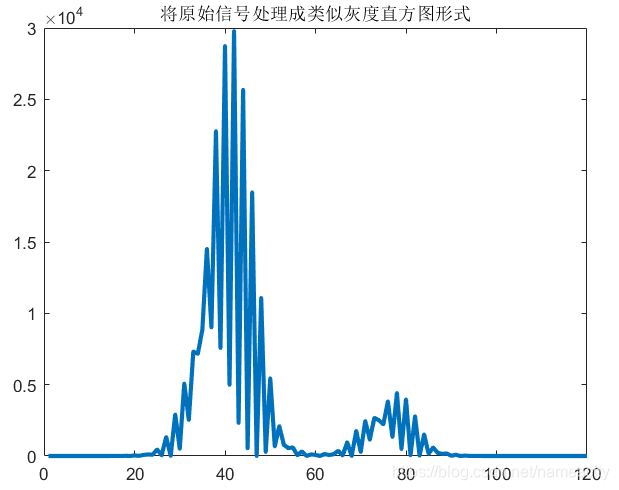
对新的信号采用大津法进行阈值分割，得到分割点：
代码如下：

[M,N]=size(I_gray);
total=sum(I_gray,2);
%总体期望
E=0;
for i=1:N
    E=E+(i*I_gray(i))/total;
end

otsu1=zeros(1,N);
otsu2=zeros(1,N);
J=zeros(1,N);
for t=1:N
    wa=0;wb=0;
    ua=0;ub=0;
    sigma_A=0;sigma_B=0;
    A=zeros(1,N);
    B=zeros(1,N);
    
    %分为A、B两部分
    for i=1:t
        A(1,i)=I_gray(1,i);
        wa=wa+I_gray(i)./total;
    end
    for j=t+1:N
        B(j)=I_gray(j);
        wb=wb+I_gray(j)./total;
    end
    
    for i1=1:t
        ua=ua+((I_gray(i1)/total)./wa)*i1;
    end
    for j1=t+1:N
        ub=ub+((I_gray(j1)/total)./wb)*j1;
    end
    
    for i2=1:t
        sigma_A=sigma_A+((I_gray(i2)/total)/wa).*(i2-ua).^2;
    end
    for j2=t+1:N
        sigma_B=sigma_B+((I_gray(j2)/total)/wb).*(j2-ub).^2;
    end
    
    otsu1(1,t)=wa*(ua-E).^2+wb*(ub-E).^2;
    otsu2(1,t)=wa.*sigma_A.^2+wb.*sigma_B.^2;
    J(1,t)=1+2*(wa.*log(sigma_A)+wb.*log(sigma_B))-2*(wa.*log(wa)+wb.*log(wb));
end

得到结果：

[value_max_Otsu1,index_max_Otsu1]=max(Otsu1)   %otsu最大/最小值对应坐标位置
[value_min_Otsu2,index_min_Otsu2]=min(Otsu2)

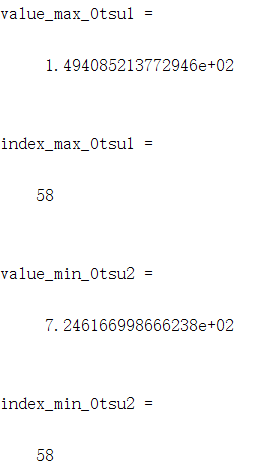
即在数据点58处（横坐标值58）取得阈值分割点，如下图，在x=58处类间方差取最大值，在x=58处类内方差取最小值：


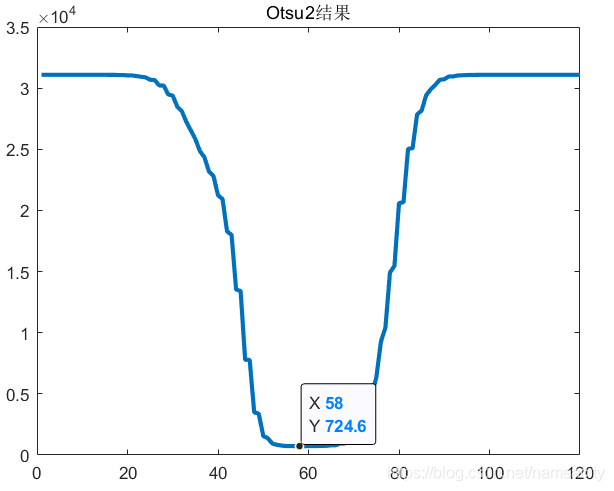
同理，OTSU算法同样可以扩展到三峰信号（含三个包络）的阈值分割，假设将信号分为三个部分，则目标方程为：
$${\delta }_b^2=w_0(u_0-u_T{)}^2+w_1(u_1-u_T{)}^2+w_2(u_2-u_T{)}^2$$

---

[1]马龙. 白光扫描干涉测量方法与系统的研究[D].天津大学,2011.