2025年7月4日学习随记

最新推荐文章于 2025-11-24 11:43:51 发布
原创 最新推荐文章于 2025-11-24 11:43:51 发布 · 943 阅读 · 31 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#学习

2025年7月4日学习随记


想学习的同学可以绕过本作者此类型文章，虽然作者的其他类型文章也不能让你学到什么。

一.目前需要补充学习的三门本科课程

1.遥感原理与应用（武汉大学出版社，国家精品课程教材）.

第二章 重点看卫星种类和高光谱类卫星，SAR卫星不用看
第八章 重点学习一下还有模式识别

2.模式识别

3.数字图像处理DIP

二.目前自学资料

1.第一优先级——GitHub pytorch基础学习https://github.com/MLEveryday/practicalAI-cn?tab=readme-ov-file
2.小土堆pytorch学习笔记

三. 每日AI问答（别管了）

1.数字图像处理和cv的关系是什么？

数字图像处理（Digital Image Processing, DIP）和计算机视觉（Computer Vision, CV）是紧密相关但目标不同的两个领域，它们的关系可概括为基础与应用、流程与系统的关系。以下是详细解析：

1. 核心定义

  • 数字图像处理 (DIP)
    专注于图像的底层操作，目标是通过算法改善图像质量、提取信息或变换表示形式。
    典型任务：

    • 去噪、锐化、对比度增强
    • 边缘检测、图像分割
    • 几何变换（旋转/缩放）
    • 压缩编码（如JPEG）

  • 计算机视觉 (CV)
    目标是让机器“理解”图像内容，并做出决策或生成高层描述。
    典型任务：

    • 目标检测（如YOLO）
    • 人脸识别
    • 3D场景重建
    • 图像语义分割（如自动驾驶中的道路识别）

2. 二者关系

(1) DIP 是 CV 的基础工具
  • 预处理依赖：CV 系统通常需要先用 DIP 技术优化输入图像。
    例如：
    • 人脸识别前需用 DIP 进行光照归一化或去模糊。
    • 目标检测前需用边缘检测突出物体轮廓。
(2) CV 是 DIP 的高层延伸
  • 目标差异：
    阶段DIPCV
    输入原始图像经 DIP 处理后的图像
    输出增强/变换后的图像或低层特征对图像内容的语义理解（如物体类别）
    核心问题“如何改进图像？”“图像中有什么？它意味着什么？”
(3) 技术流程中的协作

典型的 CV 系统流程：
原始图像
DIP预处理
特征提取
CV理解与决策
  • 步骤详解：
    1. DIP 层：去噪、归一化、边缘检测（如使用Sobel算子）。
    2. 特征提取：从预处理图像中提取关键信息（如SIFT特征）。
    3. CV 层：基于特征进行识别/分类（如用SVM或CNN判断物体类别）。

3. 关键区别

维度数字图像处理 (DIP)计算机视觉 (CV)
目标改善图像质量或提取低层特征理解图像内容并生成语义信息
输出新图像或数值特征向量标签、检测框、3D模型等高层描述
依赖数据单张图像可能需多帧图像或上下文（如视频）
典型算法直方图均衡化、中值滤波、傅里叶变换YOLO、ResNet、SLAM（同步定位与建图）

4. 实际应用中的融合

  • 医学影像：
    • DIP：增强CT图像的对比度。
    • CV：自动识别肿瘤区域。
  • 自动驾驶：
    • DIP：用图像分割分离道路/车辆。
    • CV：决策系统根据分割结果规划路径。
  • 工业检测：
    • DIP：检测产品表面的划痕（像素级分析）。
    • CV：判断划痕是否导致产品不合格（语义级判断）。

总结

  • DIP 是“修图师”：专注于图像本身的优化与特征提取。
  • CV 是“解读者”：基于 DIP 的结果理解图像含义。
  • 关系本质：

    DIP 为 CV 提供“干净、可读”的输入，CV 利用这些输入实现智能决策。
    没有强大的 DIP 基础，CV 系统难以鲁棒；没有 CV 的目标驱动，DIP 的价值无法完全释放。

两者共同构成从“像素”到“语义”的完整链条，是人工智能感知世界的核心技术支柱。

2.在研究中，不采用深度学习的方法进行研究时，一般会采用什么类型的方法?

在研究中不采用深度学习（Non-Deep Learning）时，研究者通常会依赖传统数学建模、信号处理、统计方法与经典机器学习，这些方法具有可解释性强、计算资源要求低、小样本友好等优势。以下是主要方法分类及典型应用：

一、基础图像处理技术（底层操作）

  1. 空域/频域滤波

    • 目的：去噪、增强、边缘提取
    • 方法：
      • 高斯滤波、中值滤波（去噪）
      • Sobel、Canny（边缘检测）
      • 傅里叶变换、小波变换（频域分析）
    • 应用：医学影像降噪、工业缺陷检测

  2. 形态学操作

    • 操作：膨胀、腐蚀、开运算、闭运算
    • 应用：分割显微细胞、去除文档扫描噪点

二、特征工程驱动的分析方法

1. 手工设计特征（Hand-crafted Features）
特征类型代表算法适用场景
纹理特征LBP, Haralick特征材质分类、生物组织分析
形状特征Hu矩, Zernike矩物体识别、手写字符识别
颜色特征颜色直方图, Color Moments图像检索、商品分类
局部特征SIFT, SURF, ORB图像拼接、三维重建
梯度特征HOG (方向梯度直方图)行人检测、车辆识别
2. 特征降维与选择
  • PCA (主成分分析)：压缩特征维度（如人脸识别中的Eigenfaces）
  • LDA (线性判别分析)：增强类间区分度
  • t-SNE：高维特征可视化

三、经典机器学习模型

  1. 分类/识别任务

    • 支持向量机 (SVM)：结合核函数（RBF, 多项式）处理非线性问题
    • 随机森林 (Random Forest)：多特征融合决策（如遥感图像分类）
    • AdaBoost：级联分类器（Viola-Jones人脸检测）

  2. 聚类与分割

    • K-Means：颜色量化、图像分割
    • Mean-Shift：自适应聚类（视频目标跟踪）
    • 分水岭算法：粘连细胞分割

  3. 图模型

    • 马尔可夫随机场 (MRF) / 条件随机场 (CRF)：结构化预测（图像语义分割后优化）

四、优化与数值方法

  1. 能量最小化框架

    • 活动轮廓模型 (Active Contour)：Snake算法分割器官边界
    • 图割 (Graph Cut)：交互式图像分割（如GrabCut）

  2. 变分法

    • TV (Total Variation) 去噪：保持边缘的降噪模型
    \min_u \int_\Omega |\nabla u|  dx + \lambda \|u - f\|^2

五、传统计算机视觉算法

  1. 运动估计

    • 光流法 (Lucas-Kanade / Horn-Schunck)：视频动作分析
    • 背景减除：ViBe算法实现实时监控

  2. 三维重建

    • 多视图几何：SFM (Structure from Motion)
    • 立体匹配：SGM (Semi-Global Matching) 生成深度图

六、与小样本/低资源场景的结合

  • 迁移学习：使用预定义特征（如SIFT + BoVW） + SVM
  • 集成学习：融合多个传统模型提升鲁棒性
  • 贝叶斯方法：不确定性建模（医学诊断）

传统方法 vs 深度学习的优势对比

维度传统方法深度学习
数据需求小样本有效（≤1000样本）需大规模标注数据（>10k）
可解释性数学原理清晰，特征物理意义明确"黑盒"决策，解释困难
硬件要求CPU实时运行（工业嵌入式设备）依赖GPU/TPU加速
开发周期特征设计耗时，但训练快调参复杂，训练时间长
鲁棒性可控性强，适应光照/尺度变化依赖数据分布，泛化性不稳定

典型应用场景案例

  1. 工业视觉检测

    • 方法：形态学处理 + 轮廓分析 + SVM
    • 案例：PCB板焊点缺陷检测

  2. 遥感图像分类

    • 方法：纹理特征 (GLCM) + 随机森林

  3. 医学影像分割

    • 方法：水平集 (Level Set) 演化 + 区域生长

  4. 移动端AR

    • 方法：ORB特征匹配 + RANSAC几何验证

研究趋势：传统方法与深度学习的融合

  • 混合模型：
    • CNN提取深层特征 + SVM/HMM进行决策（如人脸识别）
    • 图割优化神经网络分割边界
  • 可微分传统算子：
    • 将SIFT、形态学操作嵌入神经网络（如OpenCV的TorchVision兼容层）

📌 核心提示：在数据稀缺、安全关键型领域（医疗、航天） 或边缘计算场景，传统方法仍是首选。研究者需根据问题特性选择合适工具，而非盲目追随技术潮流。

3.全息成像记录相位的原理是什么?


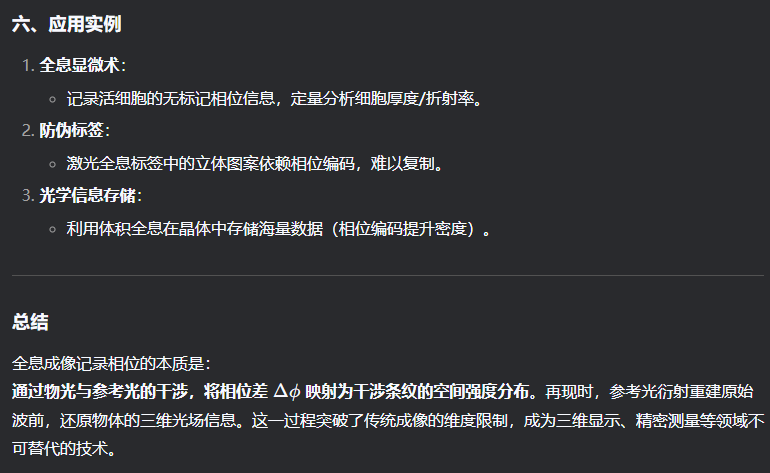
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4.光产生干涉的条件是什么？

相干波的核心是频率相同、振动方向平行、相位差恒定，三者缺一不可。

其物理本质是波叠加时干涉项的稳定性，由光源的单色性和空间扩展性决定。

激光是理想相干源，而传统方法需通过分波前或分振幅实现“人工相干”。

5.通过numpy定义的标量，数组和直接定义的变量有什么区别？

在Python中，通过NumPy定义的标量、数组与直接定义的Python变量（如int, float, list等）在数据类型、存储方式、操作效率以及功能上有显著区别。下面详细说明：

1. 数据类型

  • Python原生变量：
    • 整数：int（在Python 3中是任意精度）
    • 浮点数：float（通常是C double类型）
    • 布尔：bool
    • 序列：list, tuple 等，可以包含不同类型的元素。
  • NumPy标量：
    • NumPy定义了与Python原生类型类似但具有固定精度的标量类型，如：np.int32, np.int64, np.float32, np.float64, np.bool_等。
    • 这些标量类型是NumPy数组的单个元素。
  • NumPy数组：
    • 数组是固定类型的同质数据容器，即数组中的所有元素都是相同的数据类型（如int32、float64等）。
    • 数组类型由dtype属性指定。

2. 存储方式

  • Python原生变量：
    • 整数和浮点数等是对象，包含引用计数、类型信息等额外元数据。
    • 列表（list）是可变序列，存储的是对象的引用（指针），因此可以容纳不同类型的对象，但访问元素需要间接寻址。
  • NumPy标量：
    • 虽然是对象，但通常更轻量，并且与数组共享数据类型系统。
  • NumPy数组：
    • 数组在内存中是连续的块（一维或多维），每个元素占用的字节数固定，没有额外的对象开销（除了数组对象本身的元数据）。
    • 这种连续存储使得数组在处理大量数值数据时效率更高。

3. 操作效率

  • Python原生变量：
    • 对于数值运算，每次操作都需要进行类型检查和函数调用，因此循环执行大量操作时效率较低。
    • 列表等容器虽然灵活，但进行数值计算时需要遍历每个元素并逐个处理，速度慢。
  • NumPy数组：
    • 数组操作（向量化操作）利用C语言级别的循环，避免了Python解释器的开销。
    • 支持广播（broadcasting）机制，可以高效地对不同形状的数组进行算术运算。
    • 数学函数（如np.sin(), np.exp()）对整个数组进行高效计算。

4. 功能

  • Python原生变量：
    • 支持的操作取决于具体类型。例如，列表支持追加、插入、删除等操作。
    • 数值运算仅限于基本的算术运算。
  • NumPy标量：
    • 与数组类似，支持更多的数学函数（如三角函数、指数函数等），但通常直接使用Python数学模块或运算符即可。
  • NumPy数组：
    • 提供丰富的数组操作：形状变换、切片、索引、高级索引、聚合操作（求和、均值等）、线性代数运算、傅里叶变换等。
    • 可以方便地处理多维数据。

5. 内存占用

  • Python原生变量：
    • 整数、浮点数等标量：由于是对象，每个数值都会携带一定的元数据，因此占用的内存较大（例如，Python的int在64位系统上通常占28字节左右）。
    • 列表：除了存储数据指针，还需要额外存储列表长度、容量等信息，且每个元素都是一个独立的对象，内存占用较大且不连续。
  • NumPy数组：
    • 数组的数据部分是一个连续的、类型化的内存块，没有每个元素的额外开销。例如，一个包含1000个int32的数组只需要4000字节（约4KB）加上少量元数据。
    • 标量类型（如np.int32）占用的内存通常小于Python的int（4字节 vs 28字节）。

6. 代码示例对比

创建变量
# Python原生
a = 5                   # int
b = 3.14                # float
c = [1, 2, 3, 4]        # list
# NumPy
import numpy as np
a_np = np.array(5)      # 0维数组（标量数组）
b_np = np.array(3.14)   # 0维数组
c_np = np.array([1,2,3,4])  # 1维数组
d_np = np.int32(5)      # NumPy标量（32位整数）
运算效率对比
# Python列表求和
c = list(range(1000000))
%timeit sum(c)          # 慢，因为每次迭代都是Python对象操作
# NumPy数组求和
c_np = np.arange(1000000)
%timeit np.sum(c_np)    # 快，C语言级别循环
类型差异
# Python整数运算不会溢出（自动转换为大整数）
a = 10**1000  # 可以表示非常大的整数
# NumPy固定类型会溢出
a_np = np.int32(10**9)  # 32位整数范围约为-2e9到2e9
a_np * 10                # 溢出，结果错误（但不会自动提升类型）

总结

特性Python原生变量NumPy标量NumPy数组
类型动态类型（任意精度）固定精度（如int32, float64）同质、固定类型
存储对象，内存不连续轻量对象连续内存块
效率操作慢（解释器开销）比原生快但不如数组向量化操作，高效（C级别）
功能基本操作支持数组的数学函数丰富操作（广播、线性代数等）
内存占用较大（每个对象有元数据）较小（但比原生数组元素大）小（连续存储，无额外开销）
适用场景通用编程与数组混合使用数值计算、科学计算
因此，在科学计算和数据分析中，处理大量数值数据时应优先使用NumPy数组以获得高性能和丰富功能。而Python原生类型在通用编程和需要动态类型、任意精度时更为合适。

在 NumPy 中定义的标量、数组与 Python 直接定义的变量在内存结构、数据类型、计算效率和功能支持上有本质区别。以下是详细对比：

一、内存结构与数据类型

特性Python 原生变量NumPy 标量NumPy 数组
内存模型对象指针 (PyObject*)包装的 C 类型连续内存块 + 元数据头
存储方式分散存储独立内存单元连续内存块
类型系统动态类型 (int/float 自动转换)固定类型 (np.int32/np.float64)同质类型 (所有元素类型相同)
示例a = 5 (Python int)b = np.int32(5)c = np.array([1,2,3])
内存开销较大 (约 24-28 字节)较小 (4-8 字节 + 元数据)极小 (仅数据 + 元数据)

内存布局对比：

# Python 列表
py_list = [1, 2, 3]  # 内存: [ptr1, ptr2, ptr3] → 三个独立int对象

# NumPy 数组
np_arr = np.array([1, 2, 3], dtype=np.int32)  
# 内存: | 1 | 2 | 3 | (连续4字节×3)

二、计算效率差异

1. 标量运算
# Python 原生
a, b = 5, 3
%timeit a * b  # 100 ns 级别

# NumPy 标量
x, y = np.int32(5), np.int32(3)
%timeit x * y  # 200 ns 级别 (有对象开销)
2. 数组运算 (100万元素)
# Python 列表
py_list1 = list(range(10**6))
py_list2 = list(range(10**6))
%timeit [a*b for a,b in zip(py_list1, py_list2)]  # ~100 ms

# NumPy 数组
np_arr1 = np.arange(10**6)
np_arr2 = np.arange(10**6)
%timeit np_arr1 * np_arr2  # ~1 ms (快100倍)

加速原理：NumPy 使用 SIMD 指令 (如 AVX) 并行处理连续内存数据

三、功能特性对比

1. 类型精度控制
# Python 自动升级
a = 10**20; b = 10**20 + 1
print(a == b)  # False (正确)

# NumPy 固定类型
x = np.int32(2147483647)  # 最大int32
y = x + 1
print(y)  # -2147483648 (溢出)
2. 广播机制 (NumPy 特有)
arr = np.array([[1,2], [3,4]])
scalar = np.int32(10)
print(arr * scalar) 
# [[10 20]
#  [30 40]] (自动广播)
3. 向量化函数
# Python 需循环
angles = [0, np.pi/2, np.pi]
sines = [math.sin(x) for x in angles]

# NumPy 向量化
np_angles = np.array(angles)
np_sines = np.sin(np_angles)  # 单次调用C函数

四、特殊行为差异

1. 比较操作
# Python 列表比较
print([1,2] == [1,2])  # True (值比较)

# NumPy 数组比较
arr1 = np.array([1,2])
arr2 = np.array([1,2])
print(arr1 == arr2)    # [True True] (逐元素比较)
print(arr1 is arr2)    # False (对象不同)
2. 切片复制行为
# Python 列表切片
lst = [1,2,3]
sublist = lst[:]  # 创建新列表

# NumPy 数组切片
arr = np.array([1,2,3])
subarr = arr[0:2]  # 创建视图 (共享内存)
subarr[0] = 99     # 修改原数组
print(arr)         # [99, 2, 3]

五、适用场景总结

场景推荐使用原因
单次标量计算Python 原生变量无额外开销
大规模数值计算NumPy 数组内存连续+向量化加速
类型敏感计算NumPy 标量/数组精确控制数据类型
混合类型数据存储Python 列表/字典NumPy 要求同质元素
需要广播机制NumPy 数组自动维度扩展
内存敏感场景NumPy 数组紧凑存储 (无指针开销)

六、内存占用实测 (Python 3.9)

import sys
import numpy as np

# Python 整数
py_int = 5
sys.getsizeof(py_int)  # 28 bytes

# NumPy 标量
np_scalar = np.int32(5)
sys.getsizeof(np_scalar)  # 32 bytes (含对象开销)

# 数组内存 (1000个元素)
py_list = list(range(1000))
sys.getsizeof(py_list) + sum(sys.getsizeof(x) for x in py_list) 
# ~35,000 bytes (含指针开销)

np_arr = np.arange(1000, dtype=np.int32)
np_arr.nbytes  # 4,000 bytes (仅数据)

💡 关键结论：
NumPy 的核心优势在于连续内存布局和向量化操作，适合数值计算；
Python 原生变量在灵活性上更优，但计算效率低。
实际项目中常混合使用：用 Python 控制逻辑，用 NumPy 处理数值计算。

7.python原生变量和numpy定义的数值可以直接进行加减运算吗？

是的，Python 原生变量和 NumPy 定义的数值可以直接进行加减运算，但需要注意 类型转换规则 和 行为差异。以下是详细说明：

一、基本运算行为

1. NumPy 标量 vs Python 原生变量
import numpy as np

# Python 整数 + NumPy 标量
py_int = 5
np_scalar = np.int32(3)
result = py_int + np_scalar

print(result)         # 8
print(type(result))   # <class 'numpy.int32'> → 结果为NumPy类型
2. NumPy 数组 vs Python 原生变量
# Python 浮点数 + NumPy 数组
np_arr = np.array([1, 2, 3])
py_float = 0.5
result = np_arr + py_float

print(result)         # [1.5 2.5 3.5]
print(type(result))   # <class 'numpy.ndarray'> → 广播为数组

二、类型转换规则

运算结果的类型由 更高精度的类型 决定：

a = np.int8(10)     # 8位整数
b = 3.14            # Python浮点数
c = a + b           # 结果类型为np.float64
print(c, type(c))   # 13.14 <class 'numpy.float64'>
类型升级优先级（从低到高）：

bool → int8 → int16 → int32 → int64 → float32 → float64 → complex

三、特殊注意事项

1. 溢出行为
# Python自动升级大整数
py_big = 2**100   # Python int自动处理大数

# NumPy固定类型
np_int = np.int32(2147483647)  # 最大int32值
result = np_int + 1            # 溢出
print(result)  # -2147483648 (错误结果)
2. 数组广播机制
arr = np.array([[1,2], [3,4]])
py_val = 10

# 标量广播到整个数组
print(arr + py_val)
# [[11 12]
#  [13 14]]
3. 类型不一致的陷阱
# Python整数除法 vs NumPy整数除法
print(5 / 2)           # 2.5 (Python真除法)
print(np.int32(5) / 2) # 2.5 (结果为float)

print(5 // 2)          # 2 (Python整除法)
print(np.int32(5) // 2) # 2 (结果仍为int32)

四、性能差异

混合运算有额外类型转换开销：
import timeit

# 纯Python运算
t_py = timeit.timeit('a + b', setup='a=5; b=3.2', number=10**7)
# 约0.3秒

# NumPy混合运算
t_np = timeit.timeit('a + b', setup='import numpy as np; a=np.int32(5); b=3.2', number=10**7)
# 约1.2秒 (慢4倍)

建议：在循环中避免频繁混合运算

五、最佳实践

1. 需要精确控制类型时
# 显式转换后再运算
py_val = 3.1416
np_val = np.float32(py_val)  # 转为32位浮点
2. 避免整数溢出
# 大数运算使用Python原生类型
big_num = 10**18
np_arr = np.array([1,2,3], dtype=np.int64)
result = big_num + np_arr  # 安全
3. 性能敏感代码
# 将Python值转为NumPy后再批量运算
np_scalars = np.array([py_val1, py_val2])  # 先转换
result = np_scalars + np_arr               # 纯NumPy运算

总结

特性Python原生 + NumPy
是否支持运算✅ 直接支持
结果类型NumPy类型优先
性能有转换开销 (避免在循环中使用)
安全性注意整数溢出风险
推荐场景一次性计算/脚本
避免场景高性能循环/精确类型控制环境

💡 核心原则：
混合运算在便捷性和兼容性上表现优秀，但在性能关键路径和类型敏感场景下，建议统一使用NumPy类型进行运算。

2015年8月整理笔记本随记.ppt
11-16
这篇随记内容涵盖了多个教育和德育相关的知识点，深入探讨了教育的本质、电子智慧教育的定义、学生文化的理解以及班主任的角色。以下是对这些知识点的详细解释： 1. **教育理念**： - "精准，精减，精彩"：这强调...
vue学习随记.zip_vue_vuex_vue学习知识点笔记_图片上传插件封装
09-23
vue的知识点干货，从路由到vuex的知识点干货
2025年全国火车站经纬度信息数据
qq_38192105的博客
04-19 4412
纯前端+高德JS API获取全国火车站经纬度信息，对于生成的文件数据，可直接私聊我获取
Linux随记（十六）
Nightwish5的博客
03-22 1090
遇到的“坑”： 最初在/etc/ssh/sshd_config修改Ciphers ，但没效果，复扫仍有漏洞。这个操作系统是el8系的。他/etc/ssh/sshd_config里面的cipher描述说 在这里改是没效果的。ExecStart里面的 -启动项$CRYPTO_POLICY会覆盖它。（bclinux 8.2 和 bclinux 8.6都是这种情况。参考：https://blog.youkuaiyun.com/weixin_44800629/article/details/144770022。
Linux随记（十七）
Nightwish5的博客
04-21 403
网上参考处理方法：修改kernel.pid_max的值。【但这边输入任何指令，都没反应，最后只能重启服务器了。在黑窗口登录root，modues is unknwon, 但此时可以通过ssh登录到服务器，
Linux随记（十四）
Nightwish5的博客
01-09 1555
【代码】Linux随记（十四）
Linux随记（九）
Nightwish5的博客
05-06 1362
注意事项：无外网/离线环境下，所需的bclinux euler的rpm包。
Linux随记（二十二）
Nightwish5的博客
08-12 321
虚拟机测试情况 - 正常：
【Paper Tips】随记5-期刊投稿阶段说明
lxlyhwl的博客
03-31 2081
时间周期总结根据下述已投稿反馈，平均Accept周期为：4 months结合小木虫论坛得反馈，平均周期在4~5个月左右，算是比较快了。投稿建议总结①尽量代码开源。这样无形会增加审稿人对你实验结果的可信度。②建议引用投稿期刊的文献。会让人审稿人觉得与期刊符合度较高。即时订阅邮箱信息，第一时间知晓论文审阅动态。回复审稿人意见需要充分且礼貌。
Python基础入门篇学习随记
fengge704的博客
09-24 2286
常用的脚本语言有：PHP、JavaScript、Perl、Ruby、R语言等。记事本、终端、pytharm、vscode等。本笔记主要使用终端和vscode模式环境写第一个python语句：1、终端(每输入一条回车) 2、IDE模式 输出结果： 这种方式是写完所有代码解析器逐行进行解析，ide编辑器是需要使用print输出的，如果直接写个变量的话会报错。现在对这些代码不明没关系，先了解下，今后的例子将采用这两种方式进行。变量是变成语言中用来存和表示数据的一种抽象的概念，它们用于给数据或数值起一个具有意义的名
#随记牛客sql题-牛客1-87题 实际74题
qq_43031303的博客
03-11 1608
#随记牛客sql题-牛客1-87题 实际74题 1、查找最晚入职员工的所有信息 select * from employees order by hire_date desc limit 1 select * from employees where hire_date = (select max(hire_date) from employees) 2、查找入职员工时间排名倒数第三的员工所有信息 select * from employees order by hire_date desc limit 2
学习随记：纹波噪声谐波区别
09-04
在电子学中，纹波、噪声和谐波是三个经常被提及的概念，它们通常会影响电子设备的性能与可靠性。纹波通常指的是一种周期性的或随机的交流电压成分，它叠加在直流电平之上。在额定输出条件下，这一交流电压的峰值大小...
毫米波雷达DAC1000EVM预备知识自学（笔者自学笔记——5 DCA1000EVM命令和数据格式）
mstcoder的博客
09-11 2330
相关自学笔记
毫米波雷达AWR1642BOOST代码走读学习笔记
mstcoder的博客
09-12 1961
自学
2025年7月8日学习笔记——模式识别与机器识别学习笔记——两类错误率、准确率、Neyman-Pearson决策和ROC曲线
mstcoder的博客
07-09 600
（2）用来评价和选择与分类有关的特征，通过设定不同的阈值画出单独一个特征作为指标进行分类时的ROC曲线，计算AUC并通过比较不同特征之间的AUC来得知哪个特征包含更多的分类信息。：假阳性率（真阴性的情况下判定为阳性）：真阳性率（在为真的情况下判断为真）（1）比较不同的分类决策。
python使用递归进行文件夹内容搜索
mstcoder的博客
02-05 368
python使用递归进行文件夹内容搜索 代码： #encoding=utf-8 #递归打印所有的目录和文件 import os allfiles=[] def getAllFiles(path,level): childFiles=os.listdir(path)#读出此路径下的文件 for file in childFiles:#遍历读出的文件 filepath=os.path.join(path,file)#将路径转换为绝对路径 if os.path.i
7月8日学习笔记——统计决策方法
mstcoder的博客
07-08 229
本博文内容为的第二章前半部分学习笔记。1.本章介绍在。
基于学习的人工智能（1）为什么学习？
最新发布
致力于大数据+AI 的应用创新。
11-24 276
学习是人类最重要的认知活动之一，贯穿我们的一生。出生后，我们无时无刻不在学习：从父母那里学说话，自己尝试走路，从小伙伴那里学会折纸飞机，从老师那里学到语文、数学等各种知识。研究人员始终将光源和风扇放在同一侧，经由学习，玉米幼苗逐渐学会了“有风的地方就会有光”的规律。之后，研究人员移去光源，并改变风扇方向，玉米幼苗依然按照所学知识，向风扇方向生长。1959 年，美国计算机学家亚瑟·塞缪尔设计了一款可以自我学习的跳棋程序，并将这一新方法称为“机器学习”，从而开启了机器自我学习的道路。
开发随记
09-10
开发相关随记包含多个方面： - **软件开发**：在增加和设计较为庞大的程序时，要考虑程序结构设计，如解耦、层与层接口、模块之间关系、参数、ram、flash、运行速度等。还可学习了解aoutosar的分层结构。新的项目需...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值