2025年7月8日学习笔记——模式识别与机器识别学习笔记——两类错误率、准确率、Neyman-Pearson决策和ROC曲线

一.两类错误率

1.第一类错误（Type I Error）

• 别名：假阳性（False Positive）/“拒真错误”
• 定义：当原假设（H₀）为真时，错误地拒绝它
• 现实场景：
  • 无罪的人
• 关键特性：
  • 概率记为 α（显著性水平）
  • 研究者通过设定 α（通常为 0.05）直接控制风险
  • α 越小，拒绝真实原假设的难度越大

---

2. 第二类错误（Type II Error）

• 别名：假阴性（False Negative）/“取伪错误”
• 定义：当原假设（H₀）为假时，未能拒绝它
• 关键特性：
  • 概率记为 β
  • 受样本量、效应量和 α 值影响
  • 通过 功效（Power） 间接控制：

---

两类错误对比表

特征	第一类错误（Type I）	第二类错误（Type II）
统计定义	错误拒绝真原假设	错误接受假原假设
概率符号	α	β
研究者控制	直接（设定 α 水平）	间接（通过样本量/效应量）
核心风险	得出不存在的效果	错过真实存在的效果
降低方法	减小 α（如从 0.05→0.01）	增加样本量或提高效应量
与功效关系	无直接关联	功效 = 1 - β

---

二.准确率

三.链接: Neyman-Pearson决策

四.ROC曲线

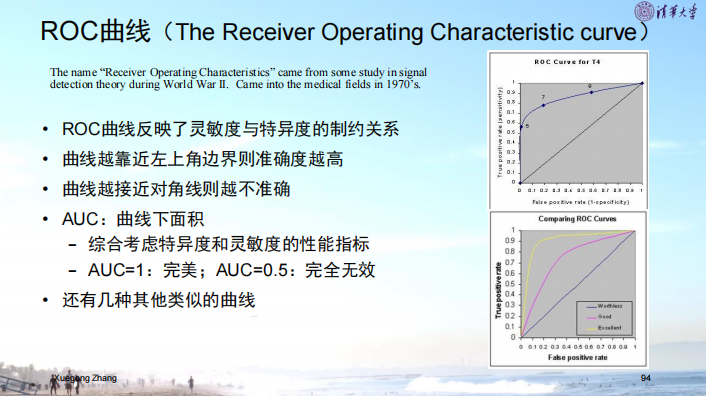
1.纵坐标：真阳性率（在为真的情况下判断为真）
横坐标：假阳性率（真阴性的情况下判定为阳性）
2.用途：
（1）比较不同的分类决策。
（2）用来评价和选择与分类有关的特征，通过设定不同的阈值画出单独一个特征作为指标进行分类时的ROC曲线，计算AUC并通过比较不同特征之间的AUC来得知哪个特征包含更多的分类信息。