透视形变及其校准的方法

透视形变(perspective distortion)描述的是，同样大小的物体，离镜头越近的物体看起来更大，反之看起来越小，如下两图所示。这种效果不自觉地被拍照者所使用，以拍出不一样的感觉。在近距离拍摄时，广角镜头的这种透视效果尤为明显，

而超过了一定的拍摄距离，透视形变则主要由距离主导——在同一距离，拍摄同一场景，无论用什么镜头，拍到的透视变形都是完全相同的。

人脑看到这样的场景时，自然而然的知道这些是透视形变，也在潜意识里强调，一条马路一般宽度相等，一辆列车，车门大小都是相同的，并且以此确定物体之间的相对距离。

原本平行的两条马路边线，在成像中不再平行，两者会有一个汇聚的点，称为“灭点”。

与透视形变相对的校正方法是图像处理中的几何空间校正，具体来说是映射变换（projective transformation）也叫平面单应(planar homography)。接下来的内容参考这篇博文，也是在学习加上看文献的理解。

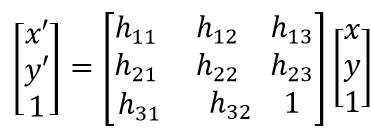
简写为：

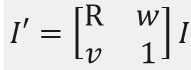
单应性矩阵有8个自由度，需要4组点，8个方程进行求解。解方程还是比较复杂的，很多博文都提到了如下矩阵：

并且在几年前有研究者尝试通过求逆矩阵解方程的方法求解单应性矩阵，并且实现图像的投射，并且达到了不错的效果，但是，执行效率非常低。使用matlab或opencv封装好的函数会好很多。以OPENCV为例，对于200万像素彩色图片，求逆矩阵的时间大约是0.4us，投射变换的时间是14ms，基本可以做到实时，而如果是灰度图像，变换时间可以压缩到4ms以内，再运行其他复杂算法完全不在话下。

先贴代码了，具体介绍就放在注释里。

import cv2
import numpy as np
import matplotlib.pyplot as plt
import time

img = cv2.imread('shusongdai.jpg')
img = cv2.cvtColor(img,cv2.COLOR_RGB2GRAY)
m,n = img.shape
plt.figure()
#plt.subplots(121) # 这里不使用subplot是因为显示会崩，具体原因不清楚
plt.imshow(img,cmap='gray') # 不加,cmap='gray'的话，显示是黄绿色的。。
#plt.imshow(img)
# 得到点击位置
pos = plt.ginput(4)

inputpos = np.float32(np.array(pos))
print('input pos:',inputpos) # 鼠标在图片中选择四个点
width =  np.sqrt(np.square(inputpos[3,0]-inputpos[2,0])+np.square(inputpos[3,1]-inputpos[2,1]) )
hight = np.sqrt(np.square(inputpos[2,1]-inputpos[0,1])+np.square(inputpos[0,0]-inputpos[2,0]) )
print(width,hight)
# 以左侧两点和底边的实际像素数为高和宽，作为投影后的画布
canvaspoints = np.float32([[0,0],
                           [width,0],
                           [0,hight],
                           [width,hight]])
start = time.perf_counter()
perspectiveMatrix = cv2.getPerspectiveTransform(inputpos,np.array(canvaspoints) )
end = time.perf_counter()
print("获取转换矩阵耗时：%s Seconds"%(end-start))
# print(perspectiveMatrix)
start = time.perf_counter()
perspectiveImg = cv2.warpPerspective(img,perspectiveMatrix,(width,hight))
end = time.perf_counter()
print("投射变换耗时：%s Seconds"%(end-start))
# plt.subplots(122)
plt.figure()
plt.imshow(perspectiveImg,cmap='gray')
plt.show()