分类预测 | MATLAB基于四种先进的优化策略改进蜣螂优化算法(IDBO)的SVM多分类预测

原创于 2025-10-08 21:59:21 发布 · 806 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #分类 #matlab

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎 往期回顾关注个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码及仿真咨询内容私信。

🔥 内容介绍

在人工智能与机器学习领域，多分类预测任务广泛存在于图像识别、故障诊断、生物信息学等关键场景。支持向量机（SVM）作为经典的分类模型，凭借其在小样本、高维数据场景下的优异泛化能力，成为多分类任务的重要工具。然而，SVM 的分类性能高度依赖于惩罚参数（C）和核函数参数（如高斯核的 σ）的选择，传统参数寻优方法（如网格搜索、随机搜索）存在效率低、易陷入局部最优的问题。

蜣螂优化算法（Dung Beetle Optimization Algorithm，DBO）是受自然界蜣螂滚粪球、挖掘和繁殖行为启发提出的新型群智能优化算法，具有收敛速度快、全局搜索能力强的特点。但原始 DBO 在处理复杂优化问题时，仍存在后期收敛精度不足、易出现早熟收敛的缺陷。为此，本文提出引入四种先进优化策略对 DBO 进行改进（记为 IDBO），并将其用于 SVM 多分类模型的

⛳️ 运行结果

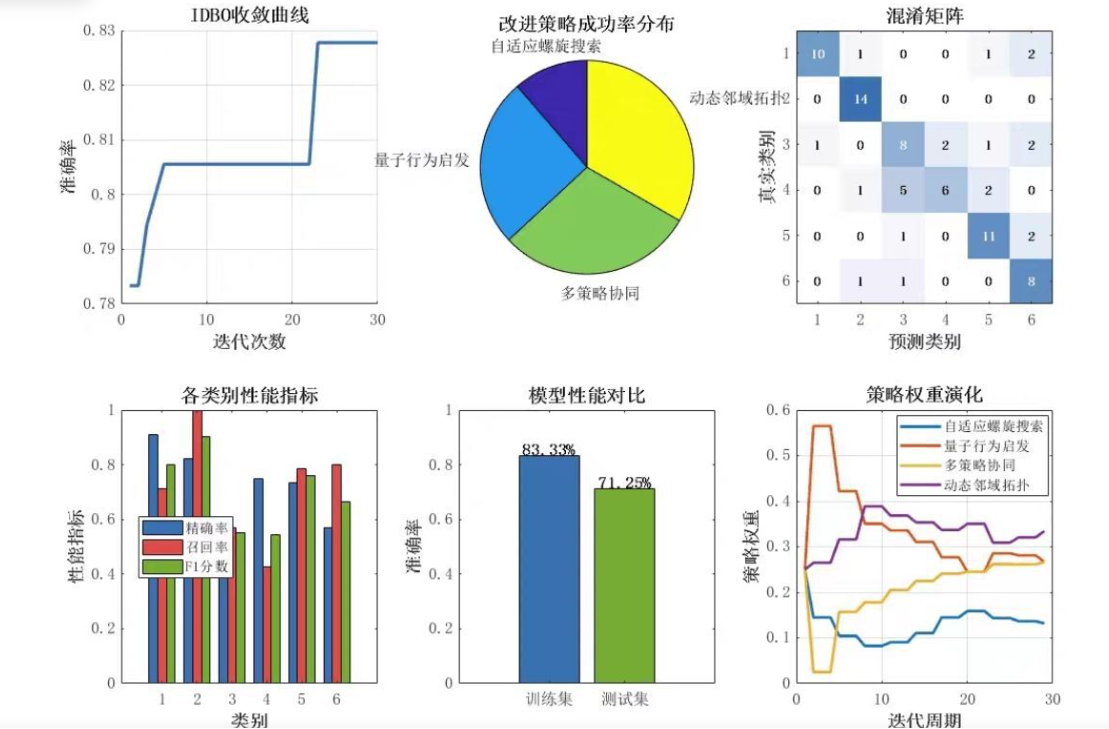
📣 部分代码

% -----------------------------------------------------------------------------------------------------------

% Dung Beetle Optimizer: (DBO) (demo)

% Programmed by Jian-kai Xue

% Updated 28 Nov. 2022.

% This is a simple demo version only implemented the basic

% idea of the DBO for solving the unconstrained problem.

% The details about DBO are illustratred in the following paper.

% (To cite this article):

% Jiankai Xue & Bo Shen (2022) Dung beetle optimizer: a new meta-heuristic

% algorithm for global optimization. The Journal of Supercomputing, DOI:

% 10.1007/s11227-022-04959-6

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [ fMin ,bestX, Convergence_curve ] = DBO(pop, M,c,d,dim,fobj )

P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

pNum = round( pop * P_percent ); % The population size of the producers

lb= c.*ones( 1,dim ); % Lower limit/bounds/ a vector

ub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector

%Initialization

for i = 1 : pop

x( i, : ) = lb + (ub - lb) .* rand( 1, dim );

fit( i ) = fobj( x( i, : ) ) ;

end

pFit = fit;

pX = x;

XX=pX;

[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value

bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin

% Start updating the solutions.

for t = 1 : M

[fmax,B]=max(fit);

worse= x(B,:);

r2=rand(1);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

for i = 1 : pNum

if(r2<0.9)

r1=rand(1);

a=rand(1,1);

if (a>0.1)

a=1;

else

a=-1;

end

x( i , : ) = pX( i , :)+0.3*abs(pX(i , : )-worse)+a*0.1*(XX( i , :)); % Equation (1)

else

aaa= randperm(180,1);

if ( aaa==0 ||aaa==90 ||aaa==180 )

x( i , : ) = pX( i , :);

end

theta= aaa*pi/180;

x( i , : ) = pX( i , :)+tan(theta).*abs(pX(i , : )-XX( i , :)); % Equation (2)

end

x( i , : ) = Bounds( x(i , : ), lb, ub );

fit( i ) = fobj( x(i , : ) );

end

[ fMMin, bestII ] = min( fit ); % fMin denotes the current optimum fitness value

bestXX = x( bestII, : ); % bestXX denotes the current optimum position

R=1-t/M; %

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Xnew1 = bestXX.*(1-R);

Xnew2 =bestXX.*(1+R); %%% Equation (3)

Xnew1= Bounds( Xnew1, lb, ub );

Xnew2 = Bounds( Xnew2, lb, ub );

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Xnew11 = bestX.*(1-R);

Xnew22 =bestX.*(1+R); %%% Equation (5)

Xnew11= Bounds( Xnew11, lb, ub );

Xnew22 = Bounds( Xnew22, lb, ub );

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

for i = ( pNum + 1 ) :12 % Equation (4)

x( i, : )=bestXX+((rand(1,dim)).*(pX( i , : )-Xnew1)+(rand(1,dim)).*(pX( i , : )-Xnew2));

x(i, : ) = Bounds( x(i, : ), Xnew1, Xnew2 );

fit(i ) = fobj( x(i,:) ) ;

end

for i = 13: 19 % Equation (6)

x( i, : )=pX( i , : )+((randn(1)).*(pX( i , : )-Xnew11)+((rand(1,dim)).*(pX( i , : )-Xnew22)));

x(i, : ) = Bounds( x(i, : ),lb, ub);

fit(i ) = fobj( x(i,:) ) ;

end

for j = 20 : pop % Equation (7)

x( j,: )=bestX+randn(1,dim).*((abs(( pX(j,: )-bestXX)))+(abs(( pX(j,: )-bestX))))./2;

x(j, : ) = Bounds( x(j, : ), lb, ub );

fit(j ) = fobj( x(j,:) ) ;

end

% Update the individual's best fitness vlaue and the global best fitness value

XX=pX;

for i = 1 : pop

if ( fit( i ) < pFit( i ) )

pFit( i ) = fit( i );

pX( i, : ) = x( i, : );

end

if( pFit( i ) < fMin )

% fMin= pFit( i );

fMin= pFit( i );

bestX = pX( i, : );

% a(i)=fMin;

end

Convergence_curve(t)=fMin;

end

% Application of simple limits/bounds

function s = Bounds( s, Lb, Ub)

% Apply the lower bound vector

temp = s;

I = temp < Lb;

temp(I) = Lb(I);

% Apply the upper bound vector

J = temp > Ub;

temp(J) = Ub(J);

% Update this new move

s = temp;

function S = Boundss( SS, LLb, UUb)

% Apply the lower bound vector

temp = SS;

I = temp < LLb;

temp(I) = LLb(I);

% Apply the upper bound vector

J = temp > UUb;

temp(J) = UUb(J);

% Update this new move

S = temp;

%---------------------------------------------------------------------------------------------------------------------------

🔗 参考文献

[1] Larsson A , Carlsson C , Jonsson M ,et al.Characterization of the Binding of the Fluorescent Dyes Yo and Yoyo to DNA by Polarized-Light Spectroscopy[J].Journal of the American Chemical Society, 1994, 116(19):8459-8465.DOI:10.1021/ja00098a004.