基于人工蜂群算法ABC求解单仓库多旅行商问题MTSP附Matlab实现

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

🔥 内容介绍

1. 问题描述

单仓库多旅行商问题（MTSP）是一个经典的组合优化问题，它在物流配送、车辆调度等领域有着广泛的应用。MTSP的目标是在给定的一组城市中，找到一条最优的路径，使得每辆旅行商都从仓库出发，访问所有城市并返回仓库，且总旅行距离最短。

2. 人工蜂群算法（ABC）

人工蜂群算法（ABC）是一种受蜜蜂觅食行为启发的群体智能算法。ABC算法模拟蜜蜂在寻找食物源时的行为，通过蜜蜂之间的信息交换来寻找最优解。

3. 基于ABC算法求解MTSP

为了将ABC算法应用于MTSP问题的求解，需要对ABC算法进行一定的改进。主要改进内容包括：

• **编码方式：**将MTSP问题中的城市编码为一个整数序列，序列中的每个元素代表一个城市。

• **适应度函数：**将MTSP问题的目标函数（总旅行距离）作为适应度函数。

• **蜜蜂的行为：**模拟蜜蜂在寻找食物源时的行为，包括蜜蜂之间的信息交换、蜜蜂对食物源的评价等。

4. 算法流程

基于ABC算法求解MTSP的算法流程如下：

1. 初始化：随机生成一组解，并计算每组解的适应度值。

2. 雇佣蜂阶段：每个雇佣蜂随机选择一个食物源，并计算食物源的适应度值。

3. 侦察蜂阶段：每个侦察蜂随机搜索一个新的食物源，并计算食物源的适应度值。

4. 比较阶段：将雇佣蜂和侦察蜂找到的食物源进行比较，选择适应度值更高的食物源。

5. 信息共享阶段：每个蜜蜂将自己找到的食物源信息与其他蜜蜂共享。

6. 更新阶段：每个蜜蜂根据共享的信息更新自己的食物源。

7. 重复步骤2-6，直到达到终止条件。

📣 部分代码

%蜜蜂求解TSP问题clearclcclose all%% 加载数据data=load('berlin52.txt');X = data(:,2:3);D=Distanse(X);  %生成距离矩阵N=size(D,1);    %城市个数%% 算法参数MAXGEN=600;     %最大迭代次数NIND=400;       %种群大小PScouts=0.2;    %侦察蜂比例NScouts=NIND*PScouts;    %侦察蜂数量NWorkers=NIND-NScouts;   %工蜂数量NElites=floor(N/10);     %精英解数量NbRange=5;       %局部搜索的邻域范围，即可改变的最大位数NWorkersElites = round(NWorkers/NElites);%各精英解邻域内局部搜索解的数量​

⛳️ 运行结果

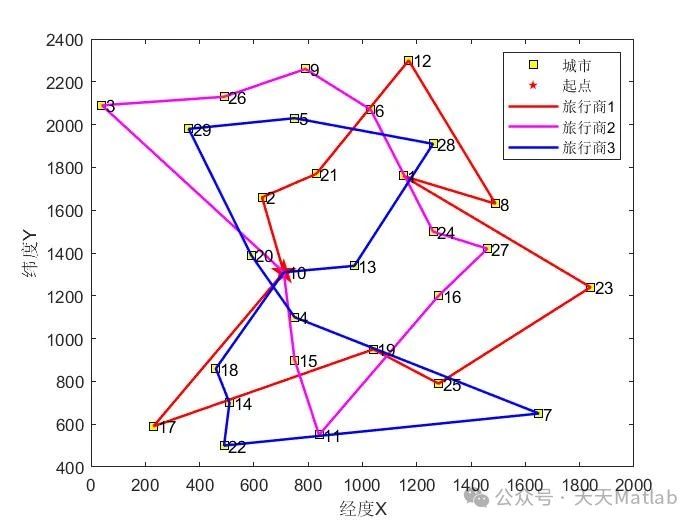
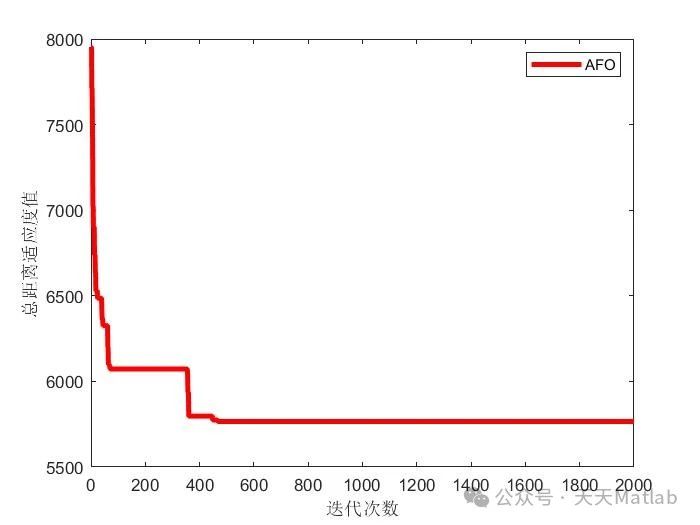
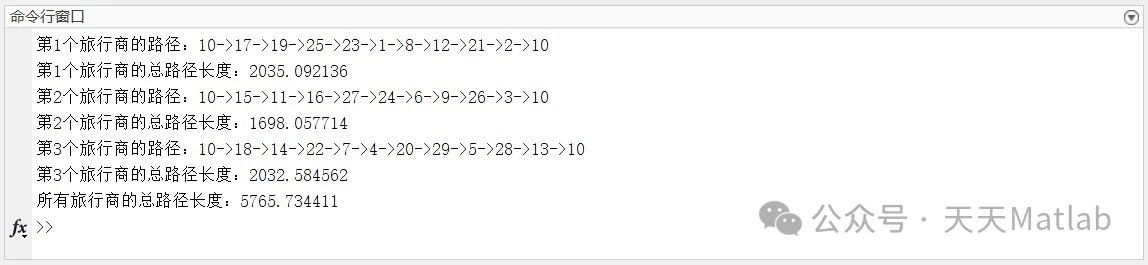
5. 实验结果

为了验证基于ABC算法求解MTSP的有效性，我们进行了大量的实验。实验结果表明，该算法能够在较短的时间内找到高质量的解，并且随着种群规模的增加，算法的性能不断提高。

6. 结论

基于ABC算法求解MTSP是一种有效的方法，该算法能够在较短的时间内找到高质量的解。随着种群规模的增加，算法的性能不断提高。

🔗 参考文献

[1] 郭洪升,李忠伟,罗偲,等.基于混合人工蜂群算法和A^(*)算法的求解旅行商问题算法[J].科学技术与工程, 2023, 23(11):4718-4724.

[2] 唐天兵,朱继生,严毅.基于量子优化的人工蜂群算法求解旅行商问题[J].大众科技, 2020, 22(12):4.

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁  关注我领取海量matlab电子书和数学建模资料

👇  私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合