欧拉函数与积性函数

wangyajie7

已于 2023-12-30 21:40:21 修改

阅读量996

点赞数 20

文章标签：算法数据结构

于 2023-12-23 21:25:49 首次发布

本文链接：https://blog.youkuaiyun.com/m0_69700299/article/details/135174360

版权

一.欧拉函数

定义：

对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目。

欧拉筛法就是求出小于等于n的所有素数的方法

具体思路：

找到一个素数后，就将它的倍数标记为合数，也就是把它的倍数“筛掉”；如果一个数没有被比它小的素数“筛掉”，那它就是素数。并且欧拉函数拥有线性的时间复杂度。

模板代码：

#include<iostream>
using namespace std;
const int N=1e8;
int p[N],cnt;
bool vis[N];
void ola(int n){
	vis[1]=1;
	for(int i=2;i<=n;i++){
		if(!vis[i]) p[++cnt]=i;
		for(int j=1;j<=cnt&&i*p[j]<=n;j++){
			vis[i*p[j]]=1;
			if(i%p[j]==0) break;
		}
	}
} 
int main(){
	ola(N);
	return 0;
}

注意：1.因为一般要筛的数字较大，所以vis数组可以使用bool类型，节省内存占用。

2.“if(i%p[j]==0) break;”这一句是优化的关键，它可以保证每个数都是被自己最小的质因子筛掉。

题目：

给定一个范围[1,n]，有q次询问，每次输出第k小的素数。

思路：直接套欧拉筛法模板。注意：由于测试样例较多，输入输出使用scanf和printf.

#include<iostream>
using namespace std;
const int N=1e8;
int p[N],cnt;
int n,q,x;
bool vis[N];
void ola(int n){
	vis[1]=1;
	for(int i=2;i<=n;i++){
		if(!vis[i]) p[++cnt]=i;
		for(int j=1;j<=cnt&&i*p[j]<=n;j++){
			vis[i*p[j]]=1;
			if(i%p[j]==0) break;
		}
	}
} 
int main(){
	scanf("%d%d",&n,&q);
	ola(n);
	while(q--){
		scanf("%d",&x);
		printf("%d\n",p[x]);
	}
	return 0;
}

二.积性函数

积性函数

指对于所有互质的整数a和b有性质f(ab)=f(a)f(b)的数论函数。

单位函数：

f(n)=[n=1]

f(n)*f(m)= 1 n=1,m=1 =f(n,m)

0 else

莫比乌斯函数：

f(n)= 1 -->n=1

-1 -->n=p1,p2.....pn

0 -->else

题目：求欧拉函数

输入n，请输出ϕ(n)的值。

代码：

#include<iostream>
#include<algorithm>
using namespace std;
int n;
int f(int n){
	int x=n;
	for(int i=2;i<=n/i;i++){
		if(n%i==0){
			x=x/i*(i-1);
			while(n%i==0) n/=i;
		}
	}
	if(n>1) x=x/n*(n-1);
	return x;
}
int main(){
	while(cin>>n&&n!=0){
		printf("%d\n",f(n));
	}
	return 0;
}

莫比乌斯与欧拉

题目描述：

给定n,T，每次在区间[1,n]中选一个数x，请输出μ(x)或ϕ(x)。

思路：

因为莫比乌斯函数是积性函数，所以可以结合欧拉筛对于每个素数直接求出值，对于其他数直接等于最小素数值的乘积

代码：

#include<iostream>
using namespace std;
const int N=1e6+5;
int n,t,q1[N],q[N],p[N],cnt x,y;
bool vis[N];
void ola(int n){
	vis[1]=1;
	q[1]=1;
	q1[1]=1;
	for(int i=2;i<=n;i++){
		if(!vis[i]){
			p[cnt++]=i;
			q[i]=-1;
			q1[i]=i-1;
		}
		for(int j=0;j<cnt&&p[j]*i<=n;j++){
			vis[p[j]*i]=1;
			if(i%p[j]==0){
				q[i*p[j]]=0;
				q1[i*p[j]]=q1[i]*p[j];
				break;
			}
			q[p[j]*i]=-q[i];
			q1[p[j]*i]=q1[p[j]]*q1[i];
		}
	}
}
int main(){
	scanf("%d%d",&n,&t);
	ola(n);
	while(t--){
		scanf("%d%d",&x,&y);
		if(x==1){
			printf("%d\n",q[y]);
		}else{
			printf("%d\n",q1[y]);
		}
	}
	return 0;
}

[SDOI2008] 沙拉公主的困惑

题目描述：
现有钞票编号范围为 1 到 N 的阶乘，但是，只发行编号与M! 互质的钞票。计算出答案对 RR 取模后的结果即可。

思路：
首先证明一个定理，gcd(a,b)=gcd(a+kb,b)
设 d=gcd(a,b) ，那么我们可以将 a 和 b 表示为：

因为 d 带走了所有的 a 和 b 的公约数，所以 k1和 k2一定互质。

设 m|(k1+k·k2) 且 m|k2 ，可知 m|k·k2。由上节课的整除的第三条性质可知：

综合一下现在的线索：

可知 m=1 。也就是说 gcd(k1+k·k2,k2)=1 ，也就是说：

证毕。那么我们现在有了 gcd(a,b)=gcd(a+kb,b)这个条件，那么接下来尝试将小于等于M! 的与 M! 互质的数字与 1~N! 范围内的与 M! 互质的数字联系起来。
假设 x ≤ M! 并且 gcd( x , M! )=1 ，那么我们就知道了如下的结论：

在本题中，x+k·M!如果大于 N! 就失去了意义，那么 k 最大能是多少？

由于 x≤ M! ，所以我们得到 k 的取值范围：

也就是说，对于每一个 x ≤ M! 并且 gcd( x , M! )=1 的数字 x ，包括它自身的话，在1~N! 的范围内，x+k·M! 都和 M! 互质，一共有 N!/M! 个 x+k·M! 。那么有多少个这样的 x 呢？φ(M!) 个。所以最终要输出的结果为：

但是 φ(M!) 很难求，因为 M! 实在是太大了。注意，这里求欧拉函数时，不能直接求 φ(M! mod R )，也就是说 φ(x) mod R ≠ φ(x mod R) mod R 。举一个简单的例子，假设R=7：

类比上节课的【线性求逆元 2】和线性求阶乘的逆元，我们想到可以尝试找到一种递推关系。假设 M 是质数，那么我们可以想到，M 这个质数一定不可能是 (M-1)! 的质因数，也就是说 M 和 (M-1)! 互质。那么既然互质，欧拉函数是积性函数，那么我们可以得到：

如果 M 是合数呢？我们根据欧拉函数的计算式分析（以下 p 都代表某个质数）：

相对于 (M-1)! ，M 并没有贡献新的质因数，所以：

所以可得：

总结一下：

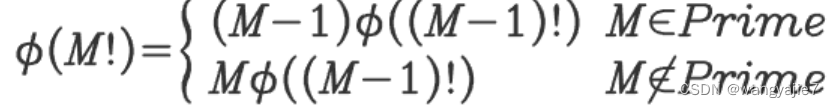
利用这个递推式，我们就可以线性求出 φ(M!) 了！首先使用欧拉筛筛出所有的素数，然后线性递推。
本题中只用到了阶乘的欧拉函数，所以我们的欧拉筛只需要判素数即可，不需要计算欧拉函数值。递推的过程如下：

#include<iostream>
using namespace std;
void init(int n){
	fac[1]=phi_fac[1]=1;
	for(int i=2;i<=n;i++){
		fac[i]=fac[i-1]*i%R;
		if(vis[i]) phi_fac[i]=i*phi_fac[i-1]%R;
		else phi_fac[i]=(i-1)*phi_fac[i-1]%R;
	}
}
int main(){
	
	return 0;
}

fac 存逆元，phi_fac 存逆元的欧拉函数值，有了这些信息，我们在 main 函数中就能直接算出结果：

#include<iostream>
using namespace std;
int main(){
	scanf("%lld%lld",&n,&m);
	if(R<=n){
		printf("0\n");
		continue;
	}
	printf("%lld\n",fac[n]*qpow(fac[m],R-2,R)%R*phi_fac[m]%R);
	return 0;
}

写完发现，上面的代码并不能过本题，结果为答案错误。哪里出了问题？
我们想到，最终答案求的是：
所以在之前的代码中，如果 R < N ，可知 N! 一定是 R 的倍数，所以我们认为这个结果一定是 0 ，所以写了个特判。真的是这样吗？
有一种特殊情况，N!和 φ(M!) 中有 R 这个因子，M! 也有 R 这个因子，但是 N!φ(M!) 中的 R 的数量和 M! 中的 R 的数量相等，正好抵消掉了。
N!中 R 的数量一定大于等于 M!中 R 的数量。如果 N!和 φ(M!)中的 R 的数量和 M!中的 R的数量相等，那么结果和 R 无关。如果大于，那么直接输出 0 即可。因为大于的情况，结果一定是 R 的倍数，对 R 取余一定是 0.
大于的情况容易处理，相等的情况需要再做处理。因为在相等的情况中，结果和 R 无关。但是取余的时候是 R 的倍数会变成 0 ，导致答案不正确。所以我们的代码更改为：

#include<iostream>
using namespace std;
void init(int n){
	fac[1]=phi_fac[1]=1;
	for(int i=2;i<=n;i++){
		ll x=i;
		while(x%R==0) x/=R;
		fac[i]=fac[i-1]*x%R;
		x=(vis[i]?i:i-1);
		while(x%R==0) x/=R;
		phi_fac[i]=x*phi_fac[i-1]%R;
	}
}
int main(){
	
	return 0;
}

#include<iostream>
using namespace std;
int main(){
	scanf("%lld%lld",&n,&m);
	if(n/R>m%R){
		printf("0\n");
		continue;
	}
	printf("%lld\n",fac[n]*qpow(fac[m],R-2,R)%R*phi_fac[m]%R);
	return 0;
}