拓扑排序和动态规划

一.定义

拓扑排序是一种对有向无环图进行排序的算法，它将图中的节点按照它们的依赖关系进行排序。

无环就是指没有几个节点形成环状。

有向无环图：

 有向有环图：

二.思路

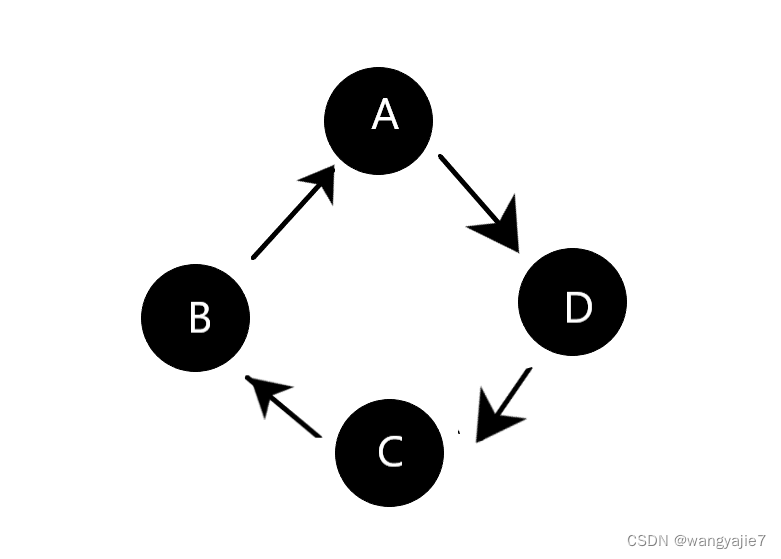
以第一幅图为例：
B的入读为0，出度为2

A的入读为1，出度为1

C的入读为1，出度为1

D的入读为2，出度为0 

所以拓扑排序就是只有从前指向后的边，没有从后指向前的边。

对这张图经行排序可以是BACD或者BCAD

想要实现这种效果，且按字典序排序（也就是只有BACD这种情况），那么我们可以使用宽搜的思路：每次把入读为0的输出，并且把与这个点有联系的点入读-1，就可以实现。要想按字典序排序，我们应该增加一定小的优化，在找入读为0的点放入优先队列中，这样就可以是队列按字典序排列。

三.练习

家谱树

题目描述：

给出每个人的孩子的信息,共n个人（1<=n<=100）。 输出一个序列a，使得每个人的后辈都比那个人后列出。

解题思路：

使用拓扑排序的宽搜思路，搭配优先队列。

代码如下：

#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int N=105;
int n,x,d[N];
priority_queue<int,vector<int>,greater<int> > q;
vector<vector<int> > e(1000);
void f(){
	for(int i=1;i<=n;i++){
		if(!d[i]) q.push(i);
	}
	while(q.size()!=0){
		int x=q.top();
		q.pop();
		cout<<x<<" ";
		for(int i=0;i<e[x].size();i++){
			d[e[x][i]]--;
			if(d[e[x][i]]==0){
				q.push(e[x][i]);
			}
		}
	}
} 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		while(cin>>x&&x!=0){
			e[i].push_back(x);
			d[x]++;
		}
	}
	f();
    return 0;	
} 

是否合法

题目描述：

多组输入，对于每组数据第一行包含两个整数，N（要测试的成员）和M（要测试的关系）（2 <= N，M <= 100）。然后是M行，每行包含一对（x，y），这意味着x是y的师傅，而y是x的徒弟。题目要求x只能是y的师傅，如果y也是x的师傅，那么这组数据不合法输出"NO"，否则输出“YES".

解题思路：

题目要求中所说的x只能是y的师傅，如果y也是x的师傅，那么这组数据不合法。也就是在这个图中不出现环，那么题目就是求输入的图是否为有向无环图。

代码如下：
 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N=105;
int n,m,x,y,d[N];
priority_queue<int,vector<int>,greater<int> > q;
vector<vector<int> > e(1000);
void f(){
	int cnt=0;
	for(int i=1;i<=n;i++){
		if(!d[i]) q.push(i);
	}
	while(q.size()!=0){
		int x=q.top();
		q.pop();
		cnt++;
		for(int i=0;i<e[x].size();i++){
			d[e[x][i]]--;
			if(d[e[x][i]]==0){
				q.push(e[x][i]);
			}
		}
	}
	if(cnt<n) cout<<"NO";
	else cout<<"YES";
	cout<<"\n";
} 
int main(){
	while(cin>>n>>m&&n!=0&&m!=0){
		for(int i=1;i<=m;i++){
	    	cin>>x>>y;
		    e[y].push_back(x);
		    d[x]++;
	    }
	    f();
	    for(int i=0;i<100;i++){
	    	e[i].clear();
		}
		memset(d,0,sizeof d);
	}
    return 0;	
}