LeetCode62-不同路径-优快云博客

本文链接：https://blog.youkuaiyun.com/lyd1995/article/details/88933497

本文探讨了LeetCode上的经典问题“不同路径”，通过组合数学原理解析了如何计算机器人从网格左上角到右下角的不同路径数量。并提供了一个C++实现方案，通过计算组合数来得出最终答案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

#LeetCode62-不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

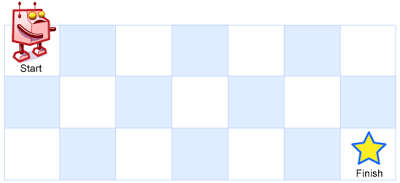
在这里插入图片描述

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

一、思路

组合数学的问题：
机器人每次只能选两个方向，假设地图的大小是 $\times m$ ，那么从左上角走到右下角需要走 $(m - 1) + (n - 1)$ 步，在这么多步中有 $(n - 1)$ 步需要向下走
因此：它往下走的方法有 $C (n + m - 2, n - 1)$ 种
当向下走的步数确定之后，这时其余的步数都只能向右走了，即确定一种走法

所以这道题是在说，如何求解 $C (n + m - 2, n - 1)$

C++代码：

class Solution {
public:
	int uniquePaths(int m, int n) {
		if (m == 1 || n == 1)
			return 1;
		int sum = m + n - 2;
		long long dividend = factorial((n > m) ? n : m, sum);
		long long divisor = factorial(2, (n > m) ? (m - 1) : (n - 1));
		int ans = dividend / divisor;
		return ans;
	}
	long long factorial(int begin, int end) {
		long long product = 1;
		while (begin <= end) {
			product *= begin;
			begin++;
		}
		return product;
	}
};

执行效率：
在这里插入图片描述