天梯L2-014 列车调度 (25 分)【二分】

杪渊探骊

已于 2022-04-20 18:00:36 修改

阅读量284

点赞数 1

CC 4.0 BY-SA版权

分类专栏：思维与基础文章标签： c++ 算法

于 2022-04-20 17:59:41 首次发布

本文链接：https://blog.youkuaiyun.com/lppppppppps/article/details/124303488

思维与基础专栏收录该内容

38 篇文章

订阅专栏

该博客讨论了一个火车站列车调度的问题，目标是让列车按照编号递减的顺序从出口离开，最少需要多少条轨道。通过分析，博主提出利用二分查找策略，每次记录当前轨道中的最小值，确保大编号的列车先出站。当遇到新列车时，如果其编号小于已有的最小编号，说明需要新开一条轨道；否则，将其加入到相应轨道。博客提供了问题的解决方案和对应的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Date：2022.04.20
题意描述：
火车站的列车调度铁轨的结构如下图所示。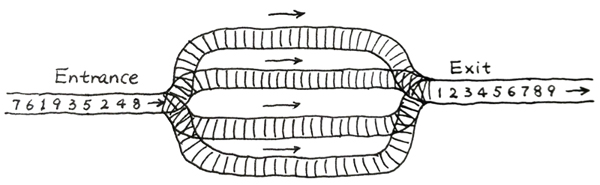在这里插入图片描述
两端分别是一条入口（Entrance）轨道和一条出口（Exit）轨道，它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入，最后从出口离开。在图中有9趟列车，在入口处按照{8，4，2，5，3，9，1，6，7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开，则至少需要多少条平行铁轨用于调度？
输入格式：
输入第一行给出一个整数N (2 ≤ N ≤10^5)，下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。
输出格式：
在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。
输入样例：
9
8 4 2 5 3 9 1 6 7
输出样例：
4

思路：不管有多少隧道，先进的必定比后进的序号大，不然就新开一条隧道。因此，我们每次只需记录当前隧道中的最小值即可，因为截止到当前隧道中的所有元素摆放都是合法的，因此也就等价于当前隧道里大的元素在靠近出口的位置而小的元素在远离出口的位置，并且为了保证出隧道是先大后小在往当前隧道里放元素时也要放比当前离着出口最远的元素更小的（否则就新开一条隧道）。因此，我们发现用一个数组记录进入每个隧道的最小元素时，随着数组下标（也就是隧道号）变大，值必然变大，显然满足二分。
因此二分找到第一个比当前元素大的元素所在的隧道号：
①找不到：新开一条隧道。
②找到了：加到这条隧道中。体现在数组中就是用当前更小值更新这个下标的元素。

代码如下：

#include <bits/stdc++.h>
using namespace std;
int cnt=0,a[100010],n,m;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x;cin>>x;
        bool flag=false;
        if(i==1) {a[++cnt]=x;continue;}
        //sort(a+1,a+1+cnt);
        int l=0,r=cnt+1;
        while(l<r)
        {
            int mid=l+r>>1;
            if(a[mid]>x) r=mid;
            else l=mid+1;
        }
        if(l>=1&&l<=cnt) a[l]=x;
        else a[++cnt]=x;
    }
    cout<<cnt;
    return 0;
}