洛谷P2327 [SCOI2005]扫雷【DP】【黄】

Date：2022.02.09
题目描述
相信大家都玩过扫雷的游戏。那是在一个n×m的矩阵里面有一些雷，要你根据一些信息找出雷来。万圣节到了，“余”人国流行起了一种简单的扫雷游戏，这个游戏规则和扫雷一样，如果某个格子没有雷，那么它里面的数字表示和它8连通的格子里面雷的数目。现在棋盘是n×2的，第一列里面某些格子是雷，而第二列没有雷，如下图：

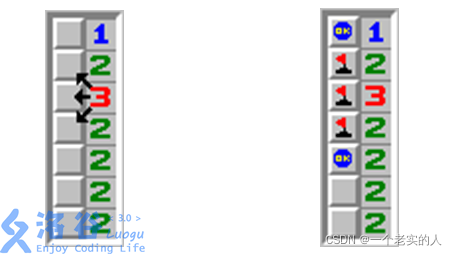
由于第一列的雷可能有多种方案满足第二列的数的限制，你的任务即根据第二列的信息确定第一列雷有多少种摆放方案。
输入格式
第一行为N，第二行有N个数，依次为第二列的格子中的数。（1<= N <= 10000）
输出格式
一个数，即第一列中雷的摆放方案数。
输入输出样例
输入 #1复制
2
1 1
输出 #1复制
2

思路：定义状态$f[i][j][k]$，表示------第$i$个格子的状态为$j$，第$i+1$个格子的状态为$k$的方案数。其中状态为0表示无雷，状态为1表示有雷。开始$f$写了个四维的，三维也一样。其中，初始化时$f[0][0][0]很显然是1$，而$f[0][0][1]$中核心点为$i==0$，但由于在矩阵外边影响不到矩阵里边，因此也算是一种可行方案，初始化也为1。
状态转移方程就要分为四类：
①$a[i]==0:f[i][0][0]+=f[i-1][0][0];$
②$a[i]==1:f[i][0][1]+=f[i-1][0][0];f[i][0][0]+=f[i-1][1][0];f[i][1][0]+=f[i-1][0][1];$
③$a[i]==2:f[i][1][0]+=f[i-1][1][1];f[i][0][1]+=f[i-1][1][0];f[i][1][1]+=f[i-1][0][1]$
④$a[i]==3:f[i][1][1]+=f[i-1][1][1];$
最终求解答案$ans$时，也是讨论最后一个格子：
①$a[i]==0:ans=f[n][0][0];$
②$a[i]==1:ans=f[n][1][0]+f[n][0][0];$
③$a[i]==2:ans=f[n][1][0];$
④$a[i]==3:不可能。$
代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
typedef long long LL;
LL n,m,a[N],f[N][3][3];
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    f[0][0][0]=f[0][0][1]=1;
    for(int i=1;i<=n;i++)
    {
        if(a[i]==0) f[i][0][0]+=f[i-1][0][0];
        else if(a[i]==1)
        {
            f[i][0][1]+=f[i-1][0][0];
            f[i][0][0]+=f[i-1][1][0];
            f[i][1][0]+=f[i-1][0][1];
        }
        else if(a[i]==2)
        {
            f[i][1][0]+=f[i-1][1][1];
            f[i][0][1]+=f[i-1][1][0];
            f[i][1][1]+=f[i-1][0][1];
        }
        else f[i][1][1]+=f[i-1][1][1];
    }
    LL ans=0;
    if(a[n]==0) ans=f[n][0][0];
    else if(a[n]==1) ans=f[n][1][0]+f[n][0][0];
    else if(a[n]==2) ans=f[n][1][0];
    //不可能三个都是1，因为角上的八个格子内最多两个雷
    cout<<ans;
    return 0;
}