机器学习基础（二）

sklearn数据集

sklearn数据

sklearn 数据API sklearn.datasets 加载获取流行数据集

获取数据的api	说明
datasets.load_*	获取小规模数据集，数据包含在datasets里
datasets.fetch_*(data_home=None)	获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录,默认是 ~/scikit_learn_data/

load*和fetch*返回的数据类型datasets.base.Bunch(字典格式)
调用先导入数据集，直接实例化即可，例如

from sklearn.datasets import load_iris

li = load_iris()
print("获取特征值")
print(li.data)
print("目标值")
print(li.target)
print(li.DESCR)

函数	说明
data	特征数据数组，是 [n_samples * n_features] 的二维numpy.ndarray 数组
target	标签数组，是 n_samples 的一维 numpy.ndarray 数组
DESCR	数据描述
feature_names	特征名,新闻数据，手写数字、回归数据集没有
target_names	标签名,回归数据集没有

数据集划分

数据集会划分	说明
训练数据	用于训练，构建模型，一般占0.75
测试数据	在模型检验时使用，用于评估模型是否有效，一般占0.25

sklearn 数据划分API sklearn.model_selection.train_test_split
from sklearn.model_selection import train_test_split

参数	含义
x	数据集的特征值
y	数据集的标签值
test_size	测试集的大小，一般为float
random_state	随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
stratify	training and test subsets that have the same proportions of class labels as the input dataset
return 训练集特征值，测试集特征值，训练标签，测试标签(默认随机取)

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

li=load_iris()
x_train,x_test,y_train,y_test=train_test_split(li.data,li.target,test_size=0.25)

如果标签为文字，可先把标签转换为数字标签

y = pd.Categorical(data['标签列名']).codes

转化器与预估器

转化器

（要求传入的数组都是二维的，一维的可用.reshape(-1,1)转换成（n_sample，1）的形式）

转化器的fit_transform	作用
fit_transform()	输⼊入数据直接转换 =fit+transform
fit()	输⼊入数据，计算当前输入数据的相关参数
transform()	进行数据的转换,分开可以用fit的数据得到的参数来transform别的数据

# 特征工程（标准化）
    std = StandardScaler()

    # 对测试集和训练集的特征值进行标准化
    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test) #注意这里是transform

有时候为了后续画图美观，我们这里会对数据进行一个排序（下面为根据Y值的排序）

order = y_test.argsort(axis=0)
y_test = y_test.values[order]
x_test = x_test.values[order, :]

按索引输出是用df.loc[order]

估计器

在sklearn中，估计器(estimator)是一个重要的角色，分类器和回归器都属于estimator，是一类实现了算法的API。

步骤	代码
实例化estimator	model=estimator()
调用fit	model.fit(x_train, y_train)
输入测试集数据	model.fit(x_test, y_test)
预测 or 评估预测准确率	1. y_predict =model.predict(x_test) 2. model.score(x_test, y_test) note:分类数据中model.score(x_test, y_test)给出的是准确率，回归给出的是$R^2$

模型选择与调优

交叉验证

为了让被评估的模型更加准确可信

将数据分成n等份，其中一份作为验证集。然后经过n次(组)的测试，每次都更换不同的验证集。即得到n组模型的结果，取平均值作为最终结果。又称5折交叉验证。

交叉验证API

*sklearn.model_selection.cross_val_score(estimator, X, y=None, , groups=None, scoring=None, cv=None)

参数	含义
estimator	估计器对象（实例化后的对象，不要设置超参数，否则就按照设置的来）
X, y=None	数据
cv	指定几折交叉验证，可用kfold进行随机的取样

PS:kfold API
sklearn.model_selection.KFold(n_splits=5,shuffle=False, random_state=None)

参数	含义
n_splitsint	default=5,Must be at least 2.
shufflebool	default=False,在k折取样前是否先随机排序
random_state	default=None,当shuffle = True, random_state 才会起作用，随机取样形成k折

网格搜索

通常情况下，有很多参数是需要手动指定的，这种叫超参数。

1. 需要对模型预设几种超参数组合。
2. 每组超参数都采用交叉验证来进行评估。
3. 最后选出最优参数组合建立模型。

网格搜索API

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)

参数	含义
estimator	估计器对象（实例化后的对象，不要设置超参数，否则就按照设置的来）
param_grid	估计器参数(dict) {“n_neighbors”:[1,3,5]}
cv	指定几折交叉验证

方法	含义
fit	输入训练数据
score	准确率

结果	含义
best_score_	在交叉验证中测试的最好结果
best_estimator_	最好的参数模型
cv_results_	每次交叉验证后的验证集准确率结果和训练集准确率结果

from sklearn.model_selection import GridSearchCV

#选一个估计器不要设置超参数，否则就按照设置的来
knn = KNeighborsClassifier()
# 构造一些参数的值进行搜索
param = {
   "n_neighbors": [3, 5, 10]}
# 网格搜索与交叉验证
gc = GridSearchCV(knn, param_grid=param, cv=2)
# 进行网格搜索
gc.fit(x_train, y_train)

print("在测试集上准确率：", gc.score(x_test, y_test))#这里的准确率和交叉验证没有关系
#在测试集上准确率： 0.9736842105263158

print("在交叉验证当中最好的结果：", gc.best_score_)
#在交叉验证当中最好的结果： 0.9285714285714286

print("选择最好的模型是：", gc.best_estimator_)
#选择最好的模型是： KNeighborsClassifier(n_neighbors=10)

print("每个超参数每次交叉验证的结果：", gc.cv_results_)
#'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 10}], 
#'split0_test_score': array([0.91071429, 0.96428571, 0.91071429]), 
#'split1_test_score': array([0.92857143, 0.875     , 0.94642857]), 
#'mean_test_score': array([0.91964286, 0.91964286, 0.92857143]),

欠拟合和过拟合

概念

拟合程度	说明	本质	原因	解决方法
过拟合	在训练数据上能够获得比其他假设更好的拟合， 但是在在训练数据外的数据集上却不能很好地拟合数据的现象。	模型过于复杂	原始特征过多，存在一些嘈杂特征， 模型尝试去兼顾各个测试数据点而导致过于复杂	1. 进行特征选择，消除关联性大的特征 2.交叉验证去发现过拟合 3.正则化
欠拟合	在训练数据上不能获得更好的拟合， 但是在训练数据外的数据集上也不能很好地拟合数据的现象。	模型过于简单	学习到数据的特征过少	增加数据的特征数量

分类算法

混淆矩阵

在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)

召回率和精确率

召回率：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）

精确率：预测结果为正例样本中真实为正例的比例（查得准）

F1-score

公式：
$$\begin{array}{rl}{F}_1& =\frac{2TP}{2TP+FN+FP}=\frac{2TP}{(TP+FN)+(TP+FP)}\\ & =2\frac{Precision\cdot Recall}{Precision+Recall}=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}\end{array}$$

$$\begin{array}{r}{F}_{\beta }=\frac{(1+{\beta }^2)Precision\cdot Recall}{{\beta }^{2}Precision+Recall}\end{array}$$

精确率准确率API

sklearn.metrics.classification_report(y_true, y_pred,labels=[label1,$\dots$ ,labeln ] , target_names=None)
return：每个类别精确率与召回率

参数	含义
y_true	真实目标值
y_pred	估计器预测目标值
label	标签列表，与标签名对应
target_names	目标类别名称，顺序与标签列表label对应

AUC(Area under curve)

$$TPR=\frac{TP}{TP+FN},FPR=\frac{FP}{FP+TN}$$

对于一个数据集进行预测，可得$TP,FNFP,TN$分布大致如下所示：

以$FPR$为横轴，$TFR$为纵轴，取不同的阈值，可做AUC曲线：

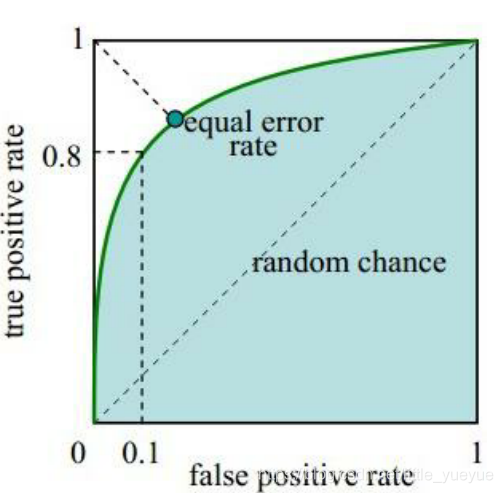
AUC越大越好的理解：每次横轴的增加，可以理解为以增加$FPR$为代价，观察$TPR$的增加效率。

k近邻算法

1. 如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。
2. 相似的样本，特征之间的值应该都是相近的。
3. 需要做标准化处理

计算距离公式

对于 a ( a 1 , a 2 , a 3 ) ， b ( b 1 , b 2 , b 3 ) a