机器学习进阶（七）贝叶斯网络

朴素贝叶斯

朴素贝叶斯的假设：对于给定分类的条件下，特征独立——每个特征同等重要(特征均衡性)，即
$$P\left(x_i\mid y,x_1,\cdots ,x_{i-1},x_{i+1},\cdots ,x_n\right)=P\left(x_i\mid y\right)$$
由贝叶斯公式，可得
$$P\left(y\mid x_1,x_2,\cdots ,x_n\right)=\frac{P(y)P\left(x_1,x_2,\cdots ,x_n\mid y\right)}{P\left(x_1,x_2,\cdots ,x_n\right)}=\frac{P(y){\prod }_{i=1}^{n}P\left(x_i\mid y\right)}{P\left(x_1,x_2,\cdots ,x_n\right)}$$
在给定样本的前提下, $P\left(x_1,x_2,\cdots ,x_n\right)$ 是常数:
$$P\left(y\mid x_1,x_2,\cdots ,x_n\right)\propto P(y)\prod _{i=1}^{n}P\left(x_i\mid y\right)$$
从而，
$$\hat{y}=\underset{y}{\mathrm{argmax}}P\left(y\mid x_1,x_2,\cdots ,x_n\right)=\underset{y}{\mathrm{argmax}}P(y)\prod _{i=1}^{n}P\left(x_i\mid y\right)$$
其中，对$P\left(x_i\mid y\right)$服从什么分布的假设不同，则有了高斯朴素贝叶斯，多项式朴素贝叶斯等等。

高斯朴素贝叶斯GaussianNB（连续）

假设某个特征服从高斯分布，即
$$P\left(x_i\mid y\right)=\frac{1}{\sqrt{2\pi }{\sigma }_y}\exp \left(-\frac{(x_i-{\mu }_y{)}^2}{2{\sigma }_y^2}\right)$$
参数可通过MLE计算

多项分布朴素贝叶斯MultinomialNB（离散）

假设某个特征服从多项式分布，即对于整体每个类别y，参数为${\theta }_y=({\theta }_{y1},{\theta }_{y2},\dots ,{\theta }_{yp})$，其中$p$为该特征的属性数，则
$$P\left(x_i=i\mid y\right)={\theta }_{yi}$$
用MLE估算参数${\theta }_y$的结果为：
θ ^ y i = N y i + α N y + α n , N y i = ∑ I { x i = i } , N y = n \hat{\theta}_{yi}=\frac{N_{yi}+\alpha}{N_y+\alpha n},N_{yi}=\sum I_{\{x_i=i\}},N_y=n θ^yi​=Ny​+αnNyi​+α​,Nyi​=∑I{xi​=i}​,Ny​=n

$\alpha =0$时，为经典MLE,$\alpha =1$时，为laplace平滑，$\alpha <1$时，为lidstone平滑，$\alpha \ne 0$可以解释为防止过拟合

生成模型

过程考虑$P\left(x_i\mid y\right)$属于什么分布$\to$生成模型
过程考虑$P\left(y\mid x_i\right)$属于什么分布$\to$判别模型

贝叶斯网络

1. 把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。
2. 贝叶斯网络(Bayesian Network)，又称有向无环图模型（无环，即不能存在这样的路径：从某个结点开始，沿着链接中箭头的⽅向运动，结束点为起点。），是一种概率图模型，根据概率图的拓扑结构，考察一组随机变量$X_1,X_2...X_n$及其$n$组条件概率分布的性质。

贝叶斯网络举例：
下图可写成$p(a,b,c)=p(c|a,b)p(b|a)p(a)$

而朴素贝叶斯的这种假设$P\left(x_1,x_2,\cdots ,x_n|y\right)={\prod }_{i=1}^{n}P\left(x_i\mid y\right)$,相当于下图，$x_1,x_2,\dots ,x_n$之间没有连接。

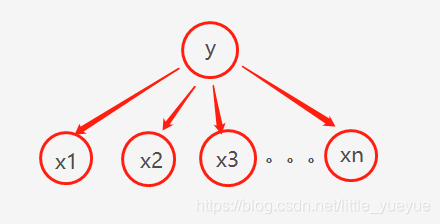
下图$x_1,x_2,\dots ,x_7$的联合分布：
$$p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3)p(x_5|x_1,x_3)p(x_6|x_4)p(x_7|x_4,x_5)$$

全部随机变量变量的联合分布为：
$$p(x_1,x_2,\dots ,x_n)=\prod _{i=1}^{n}p(x_i|parents(x_i)）$$

叶斯网络判定条件独立

下述结论可从结点推广到结点集

tail-to-tail

$$\begin{array}{rl}P(a,b,c)& =P(c)\ast P(a|c)\ast P(b|c)\\ \frac{P(a,b,c)}{P(c)}& =P(a|c)\ast P(b|c)\\ P(a,b|c)& =P(a|c)\ast P(b|c)\end{array}$$
在$c$给定的条件下，$a,b$被阻断(blocked)，是独立的。

head-to-tail

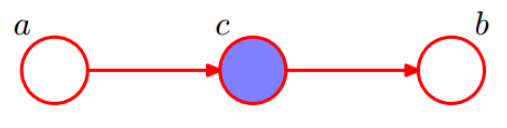
$$\begin{array}{rl}P(a,b|c)& =\frac{P(a)\ast P(c|a)\ast P(b|c)}{P(c)}\\ P(a,b|c)& =P(a|c)\ast P(b|c)\end{array}$$
在$c$给定的条件下，$a,b$被阻断(blocked)，是独立的。

head-to-head

$$\begin{array}{rl}P(a,b,c)& =P(a)\ast P(b)\ast P(c|a,b)\\ P(a,b)& =\sum _{c}P(a,b,c)=P(a)\ast P(b)\end{array}$$
在$c$未知条件下，$a,b$被阻断(blocked)，是独立的。