多媒体移动设备实时功耗控制系统
唐琼,安赫尔·M·格罗巴,爱德华多·华雷斯,Member,IEEE,塞萨尔·桑斯,Senior Member,IEEE,和费尔南多·佩斯卡多,Senior Member,IEEE
摘要
电池供电移动设备中的能耗是一个关键问题。随着任务复杂性的增加(例如广泛使用的视频解码),自主运行时间正受到越来越大的影响。尽管正在开发新型高容量电池,但用于控制(即节省)功耗的技术仍可带来显著益处。本文提出、实现并测试了一种适用于多媒体移动设备功耗调节的实时闭环控制系统。该新型闭环控制系统无需专用功率传感器,仅依赖常见移动处理器中标准配备的性能监控计数器(PMCs)。通过一种算法,利用这些计数器对功耗进行估计,并将该算法连同控制系统本身集成到操作系统中。首先建立了一个理论系统模型,以(1)支持控制器的设计,以及(2)在特定低成本开发板上对控制系统原型的实际结果进行验证。实验结果证明了控制系统的稳定性,并表明经典控制器在稳态下能够有效地将多媒体系统功耗维持在期望值附近,其调节时间短至一个采样间隔。
索引术语 — 移动多媒体,功耗控制,功耗估计反馈。
I. 引言
目前,便携式电子设备被广泛使用,其中大多数设备都具备多媒体功能。这些功能包括视频序列的采集、编码、解码和播放等,这些任务可能是最消耗能量的操作之一。这类设备。事实上,新标准的不断推出往往导致视频任务的能耗增加,因为计算成本也随之上升。例如,当将最新的高效视频编码(HEVC)[1]与较早的H.264[3]进行比较时就会出现这种情况。另一方面,由于这些移动设备依赖电池供电,其自主运行时间受限于电池充电周期的持续时间。而执行上述日益被用户需求所驱动的视频任务,会显著影响电池充电周期的持续时间。鉴于这些小型设备所用电池的能量容量预计无法以与用户需求[4]相同的速率提升,因此针对优化系统能耗的方法研究变得至关重要。
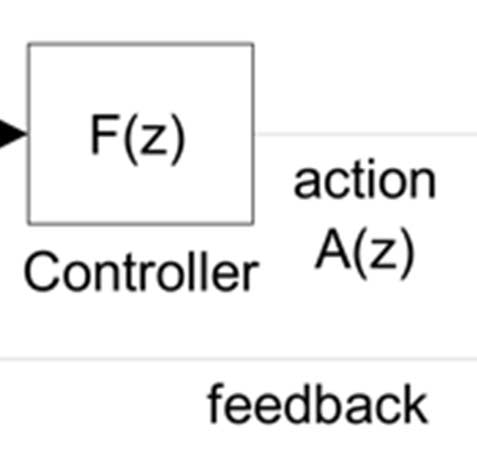
本文稿提出了一种利用系统控制理论来优化移动终端在解码视频时功耗的方法,同时明显保持合理的用户体验质量(QoE)。为此,需要构建一个闭环控制系统,其中被控设备(受控对象)为执行视频解码器的微处理器单元(MPU)。被控对象输出端的被控变量(即产生反馈信号的变量)应为其功耗,而被控对象输入端应允许控制器对被控对象输出值(即功耗)进行调节。对于被控对象输入(控制作用信号),采用MPU的动态电压频率调节(DVFS)机制,因为该机制广泛存在于多种消费类电子平台上。该机制使MPU能够在不同的工作性能点(OPPs)下运行,即不同的电压和频率对。
另一方面,本研究旨在将控制系统基于尽可能接近实际功耗的反馈信号,而无需使用在许多常见的消费类移动平台上不可用的专用功耗监测传感器。所采用的解决方案是通过常见的系统事件计数器来估计功耗。
所提出的功耗估计算法用于向控制器反馈功耗信息,其具体基于Ren et al.[5],其中,通过使用处理器性能监控单元(PMCs),将能量测量与某些合适事件的计数值进行离线关联。根据该关联关系,可获得处理器在固定OPP下解码视频时的静态能量估算。为了将该方法适配到目标控制系统,已对其进行了修改以根据视频解码器自身的工作性能点[6]和视频帧率进行响应。在后续步骤中,估计子系统在操作系统内实现,使其能够以系统采样周期{T}定期且独立于视频帧率[7]实时计算功耗估计样本,从而作为控制系统的反馈。
此外,控制器输出作用于动态电压频率调节机制以选择合适的OPP,如Qiong et al[8]中所述。
根据前述前提,并采用给定的低成本开发板作为测试平台应用平台[6]‐[8],获得了一些初步的仿真结果:首先基于实际消耗数据,且仅针对某一特定类型的积分控制器[8];其次使用平均估计值,但同样针对同类型的积分控制器[6]。在两种情况下均获得了有希望的结果,从而推动了控制系统在应用平台上的实现。所实现系统的首批实际结果已在Qiong et al. [9]中提出,结果显示不仅最初考虑的积分控制器的实测结果与仿真结果相符,其他几种线性控制器也表现出一致性。本文在此基础上进一步扩展,增加了更多文献和背景细节,更深入的严格建模、分析与设计部分,以及对更多类型控制器所得结果的更详尽比较,提炼出每种控制器在目标应用中的优缺点。
本文的结构如下:第二节比较了其他相关工作并指出了创新性;第三节概述了所提出的系统模型和控制器设计方法;第四节介绍了测试平台实现的概况;第五节描述了所进行的实验,包括其主要结果与讨论;最后,第六节总结全文并提出未来工作。
II. 相关工作
近年来,为节约能源而开展的研究和创新工作不断增加,不仅涉及小型电池供电系统[10],[11],还涵盖各种基于微处理器的领域,甚至扩展到大型网络服务器或数据中心[12],[5],[13][15],以及多媒体案例—。这些研究方向中的许多都基于启发式方法[16],[17]。
基于多媒体移动设备的节能示例之一是Kim et al.[18],其实施了一种基于负载的处理器hotplug算法。该算法周期性地监控在线核心的平均负载,并根据平均负载关闭冗余核心。然而,本文不关注多核的hotplug,而是聚焦于每个独立核心本身,旨在通过反馈实时功耗状态来实现节能。由于多核由多个单核组成,因此对单个核心的功耗控制是一种节能机制,可与多核hotplug算法协同工作,以增强整体节能效果。此外,事件计数器可以直接在内核级别获取,因此不会受到在用户空间运行的应用程序的限制。
另一个近期的例子将机顶盒(STB)视为一种小型多媒体设备,在智能家居中应用日益广泛。Jung et al.[15]提出了一种利用基于位图的活动日志来开启/关闭某些STB功能的节能方法。然而,在本文中,为了简化工作并专注于由微处理器单元(MPU)、内存子系统及相关输入/输出总线引起的功耗,电路板被配置为最小系统,禁用了不必要的组件。此外,被动待机模式使用以位图形式表示的活动日志来发现模式并预测下一次用户活动。类似地,Lee et al.[19]也假设采用混合模型系统来进行未来的空闲时段预测。但本文实现的工作是一种实时控制系统,能够根据用户的当前活动动态调整节能状态,从而精确满足用户需求。
为了降低嵌入式处理器的功耗,通常采用具有动态电源管理(DPM)能力的电源管理单元(PMU)。Hwang et al.[20]提出了一种PMU设计,该方法是一种基于硬件的方法,通过收集和分析程序计数器(PC)值的模式来预测下次I/O设备访问何时恢复。计数器驱动的电源管理也启发了本文中的反馈信息。此前也有针对此类估计的方法,例如Wang et al.[21]使用处理器性能监控计数器(PMCs)来估计二级缓存的功耗,或者Lively et al.[16]和Xiao et al.[22]将这些PMCs与多变量自适应回归样条(MARS)方法结合使用,以建模能耗模式。
其他示例包括Wang et al.[23]和Mishra et al.[24],其中在线性控制器被插入到反馈信号为处理器利用率因子的环路中,该因子与其功耗相关。在Garg et al.[25]等情况下,反馈信号是某些系统队列的占用情况,因为恒定的占用率意味着能耗处于最优状态。其他方法将能耗与处理器工作负载相关联,后者作为反馈信号,例如Bang et al.[26]或某些Linux cpufreq调控器。当实际功耗直接用作反馈信号时,如Wang et al.[27]和Kamat[10],系统需要配备特定的功率传感器,但这并不总是可行的。此外,Choi et al.[28]提出了一种用于移动网络语音(VoIP)设备的节能模式,Lim et al.[29]提出无线远程检查点环境中的能量感知最优检查点间隔,用户应用程序已扩展至网络,为开发节能算法提供了更广阔的空间。本文的一个创新之处在于一种精确的基于PMC的估算器,其作为控制系统中的反馈信号。该基于PMC的估算器基于通用硬件性能计数器来计算视频解码器的功耗,也可调整和改进以适用于其他设备和应用。因此,本文的方法具有可移植性和可扩展性。

此外,诸如Huang et al.[30]等能量优化方法在本文中重点讨论了功耗问题,并介绍了当无线数据包在闭环系统中实现时的功耗节省机制及功耗消耗的改进。总体到g.1。根据s的功耗,系统的功耗取决于ant。对于这种情况,采用基于特征估计的反馈方法,即在测试过程中,系统处于工作状态。
III. 模型
A. 系统模型
系统行为应基于系统的模型。在模型I中,尽管被控对象对于估计器输出而言被视为部分考虑,但使用它会导致提出的数学模型适用于微处理器单元,从而产生近似。基于微处理器单元的功耗/能量创新性,使其能够实现。
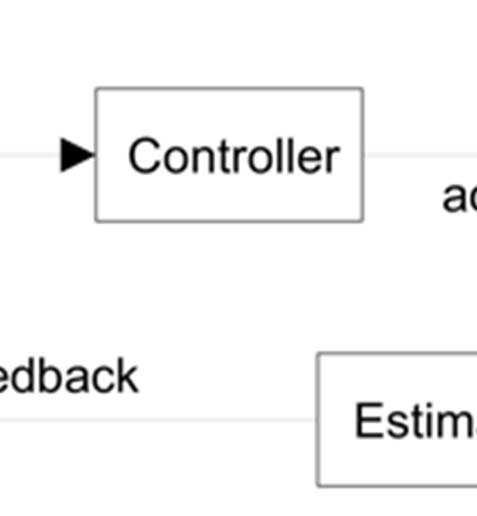
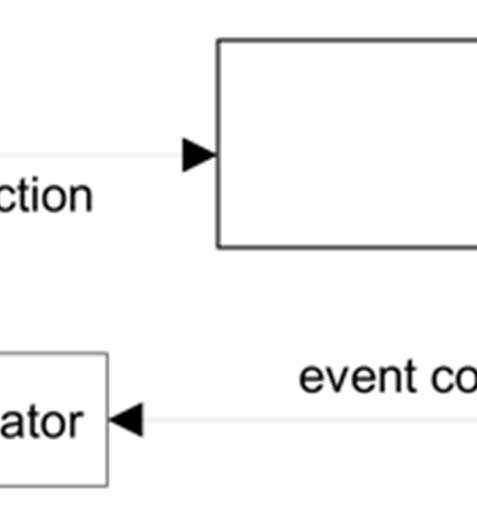
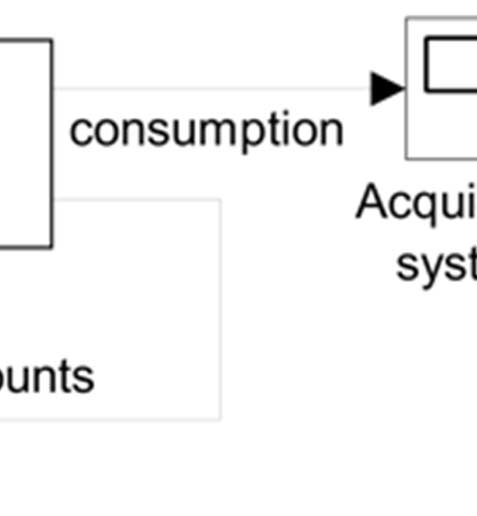
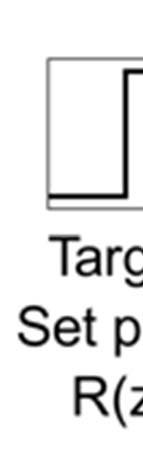
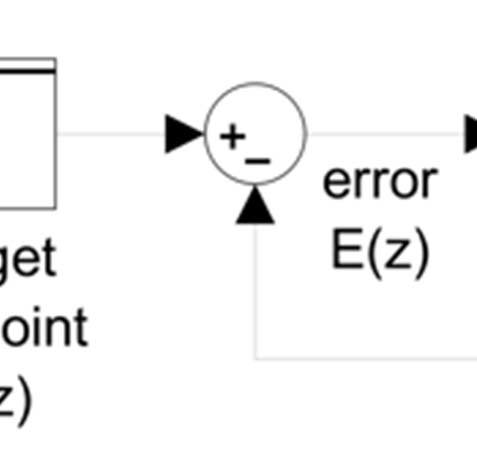
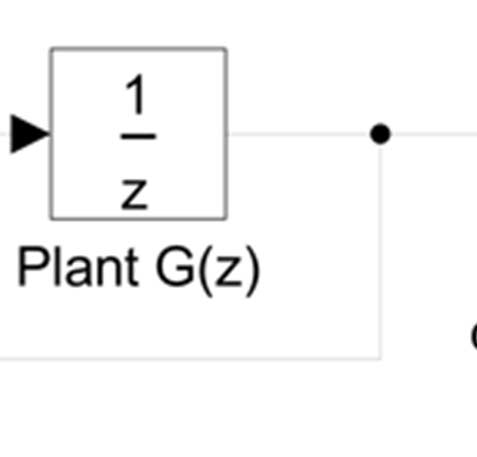
所提出方法的近似反馈系统模式旨在调节设定点(目标值),使其接近每个工作点的需求,并抑制波动(干扰)。为此,系统采用基于误差的反馈机制。如前所述,执行器结构通常包括PMCs和DVFS。图1显示了一个采集阶段的流程,以便系统正确运行。
被控对象的层级包括MP,出于拓扑结构考虑,将被控对象外部的部分与被控对象结合,形成更复杂的建模方法,其中包含被控对象,并进行建模分析。控制器actor在被控对象之间,如引言部分所述,向系统提供可用的VFS信息,以确认采集系统。闭环c k。我们的依赖于作为系统采样周期基础的系统。在此方法中,被控对象输入输出是功耗,准则移动。
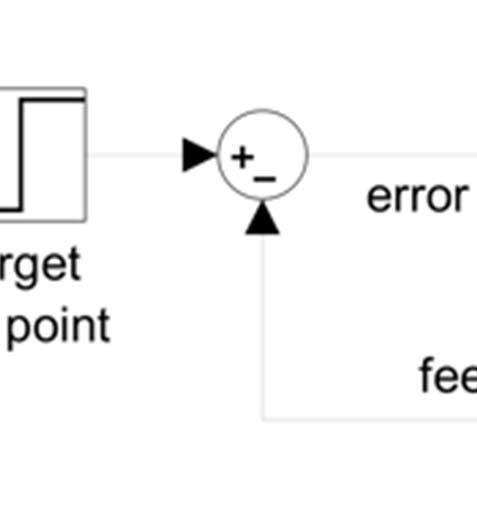
在图2中,z-1由s P步长驱动。反过来,它表示一个带有估计值的建模输出,即针对该d F(z)的建模系统,而E与R(z)计算得到,是nt。该传递函数为M(z),且它c
$$
z G( )\=
$$
从延迟来看,OPPG(1)=1、输入、m 功耗 被控对象输出由 s 称为可建模设定点系统
$$
) (z M \=
$$
B. 消耗
从控制控制比例函数P-c(最高稳定性e ss ,c 设定点较低 b 然而积分
我正在图2中解释t,clo
C概念和m
保持较低的开销,但具有足够的周期 T,可以以秒为单位。由于时间间隔较短,因此一个采样周期将已经完成。考虑到这一点,对于系统而言是有效的,这也被指出。
$$
z z A z C 1 () ()
\=
$$
在图2中,z-1 由s P步长驱动。反过来,它表示一个带有估计值的建模输出,即针对该d F(z)的建模系统,而E与R(z)计算得到,是nt。该传递函数为M(z),且它c
$$
( 1 ( ) ( ) ( F z F z R z C
+ \=
$$
B. 控制器设计
从线性控制器可以进入系统。比例(P)控制器的增益M P (z)=K P /(z+controller g aint 为正)导致输出为K Pc =1。可通过公式计算,对于P控制器,该值是系统的增益边界,过高则会导致不稳定。积分(I)控制器
系统设置为消耗
数学模块
头部和抖动在高频下应保持固定,在如此长的周期内,有足够的时间更新其控制。例如,在O之后的一个采样点,已有研究展示了考虑这些被控对象的情况,G(z)如图2所示。
1项在G(z)系统中用于适应n,单位化的归一化m h A(z)在(1)中,对应于t OPP中的 C(z)。消耗作为Z变换E(z)=R(z)-C(z)是期望的传递函数,可以计算
$$
) ( ) ) ( ) z G z z G
\cdot
\cdot
n
$$
模型最初设计为[33] 的最简形式。它将从 (1) 中的 KP 和 n得到系统临界增益,因为闭环在 (3) 处出现 [34] ,此时
控制器 essP =1 的误差被最大化。
为了减小并考虑消耗的影响。
图n中的拓扑结构 概念和m
k 图解的
r 效应在控制周期内,张力范围较大,单次采样足以使P计数值达到OPP步长,从而计算新的平均值。基于这一前提,采用如图所示的方法
表示其功耗估计值的静态增益模型,其中,是根据活动预期的 (1),是整个系统功耗的Z变换形式的误差 z),其中s为功耗消耗。
如上所述,闭环应用线性控制会导致系统出现(1)和(2)中的系统极点,在p稳态极限下,
百分比为100/(1+K P) 。最小值(essP) =50% 甚至可能被抵消,可以忽略不计。
嵌入式操作,或数百个样本应在任何 OPP功耗之后,PMCs的功耗,Z传递函数n
在(1)[32],
(1)
e 一个采样周期后的估计值,在G(z)之后,即被控对象的估计平均值为 OPP。
较低的估计值通过传递函数和误差序列得到系统输入,即闭环系统在(2)中的描述。
(2)
经典的线性方法用于测试滚轮,其中系统传递函数为K P 是pMP =– K P系统的稳态误差对于阶跃输入而言,因此为%,即为此误差的值。
提出了三种基于前向矩形规则(FRR)、后向矩形规则(BRR)和梯形或Tustin双线性规则(TR)的I控制器。它们对应的Z传递函数(可由Franklin et al.[32]获得)在 z=1处包含一个极点,从而确保式(3)中ess的值为零。这些控制器导出了如式(4)所示的系统传递函数,即FRR‐I对应的 MF 、BRR‐I对应的MB以及TR‐I对应的MT ,其中KF、KB和 KT分别为相应的积分增益,T为前述的系统采样周期,闭环系统极点如式(5)所示,分别为pMF、pMB和pMT 。
$$
/2 1) /2 ( 1) ( /2 ) (
1 ) ( ; ) (
2
2
T K z T K z z T K z M
T K z T K z M T K z z T K z M
T T
T T
B
B B F
F F
\cdot + - \cdot +
+ \cdot \cdot \=
\cdot + -
\cdot \= \cdot + -
\cdot \=
$$
(4)
$$
4 4 12 ) ( 2
1 ; 2 4 1 1
2
+ \cdot - \cdot \pm \cdot - \=
\cdot - \= \cdot \cdot - \pm \=
T K T K T K p
T K p T K p
T T T MT
B MB F MF
$$
(5)
之前提到的一些经典线性控制器组合也可使用。例如,比例积分(PI)甚至比例积分微分(PID)在控制领域中广为人知[33]。它们的传递函数可由Golnaraghi et al.[33]获得,在z=1处保留一个极点,从而仍能确保式(3)中ess的值为零。此外,它们包含一个(PI情况)或两个(PID情况)零点。
为了测试这两种组合中的各一种情况,固定零点的值以实现系统根轨迹[33],至少能够保证闭环系统的稳定性。因此,对于PI组合,如果选择其零点值为0,则其传递函数将类似于BRR‐I的情况。为了获得不同的行为,选择零点值为0.5,这导致根轨迹具有两个实分支,一个为正且有限,另一个为负且无限。这两个分支在单位圆内的共存使得系统稳定[33]。
对于PID组合,其两个零点选择了常见的‐1值,这导致系统根轨迹具有两条实/复分支和另一条实的、负的且有限的分支。同样,这三条分支在单位圆内的共存保证了系统的稳定性。
使用选定的零点值,两种组合的闭环传递函数M(z)在(6)式的两种情况下分别为MPI(z)和MPID(z),其中K PI 和K PID 分别为相应控制器的增益。
$$
\left( \right)
\left( \right)
\left( \right)
\left( \right) PID PID PID
PID PID
PI PI
PI PI
K z K z K z z K z M
K z K z z K z M
+ + - +
+ \cdot \=
- - +
- \cdot \=
2 1 1 ) (
0.5 1 0.5 ) (
2 3
2
2
$$
(6)
IV. 实现
A. 应用平台
本研究中所使用的嵌入式硬件/软件平台的具体细节已在之前的部分出版物[6]‐[8]中描述。如第一节所述,测试平台应用平台采用了一块低成本开发板。由于本工作的重点首先在于控制系统,因此选择该开发板时更注重易于实现动态电压频率调节和电源管理控制器访问,以及开源硬件/软件等特性,而非计算性能等因素。因此,该平台的一些主要特征如下。
它基于一种用于多媒体嵌入式系统的单处理器开发板。除了必要的内存和适当的外设外,还包括一个带有微处理器单元(MPU)和多个协处理器的多媒体处理器。该 MPU提供4个处理器性能监控计数器(PMCs)以及一个时钟周期计数器。操作系统基于Linux内核3.8.0,并打上补丁以支持通过cpufreq Linux驱动程序管理的动态电压频率调节机制。为了最小化动态电压频率调节机制中基于OPP接口的非线性效应,该开发板MPU的默认cpufreq定义已扩展至27个验证过的OPP[8]。此外,cpufreq代码还经过修改,以包含基于PMC的功耗估算器[7]以及控制系统本身[9]。该估算器和控制系统均在操作系统级别以实时采样周期T=100 ms同步运行,满足第二节.A小节中所述数学模型有效性的时序要求。实际上,控制系统产生的开销在最坏情况下也测得低于4%。
应用平台的其他部分一方面包括用户级视频解码器,即一个MPEG4‐第二部分解码器,用于解码一致性测试视频文件以维持多媒体系统的运行;另一方面包括基于PC的 GPIB连接商用设备,该设备用于为电路板供电并获取其电流消耗记录。
B. 系统模拟器
已使用一种动态系统仿真的商业工具[6]为该系统开发了仿真器。该工具允许用户开发、配置和仿真图形化框图。因此,图2的框图已通过一些修改在仿真工具中实现。
首先,它包含了一个用于居中的附加部分错误倾向P控制器的默认状态,作为一种中等OPP偏移(控制系统实现中也包含该部分);其次,在图2的控制器与被控对象之间插入了一个量化模块,以建模由仅识别27个不同级别的基于OPP的被控对象输入所引起的非线性。显然,控制器模块在每次实验中都配置了相应的传递函数。
该仿真器能够在实施功率控制系统之前预测其行为,甚至可以考虑基于非线性OPP的被控对象接口对理论线性模型所预期的系统响应造成的影响。此外,只要实际系统的结果与仿真结果相符,该仿真器也有助于验证实际系统中获得的结果。
V. 实验
A. 控制器增益的选择
第二节中提出的模型需要在第三节介绍的系统中进行测试。为此,在实现过程中一旦将采样周期固定为T=100 ms,控制器的数学传递函数就需要针对合适的增益值进行具体化。为了最大化控制系统的相对稳定性(闭环方案中的一个关键问题),理论上应使闭环系统主导极点的模尽可能小,即主导极点越深入单位圆内,系统的相对稳定性越好。在此意义上,图3根据公式(5)绘制了上述 值下三种积分控制器的主导极点模随积分增益的变化曲线。从图3可以看出,BRR‐I控制器实现了最小的系统主导极点模:min(| pMB|)=0,对应的增益为KB=10;其次,TR‐I控制器在增益为KT=3.43时达到min(| pMT|)=0.41;最后,FRR‐I控制器在KF=2.5时达到min(| pMF|)=0.5。因此,这些即为各积分控制器所选择的积分增益值。
关于PI组合,图4显示了MPI的两个极点的模数随KPI的变化情况。为了避免系统响应中出现不希望的振荡,应使正极点保持为主导极点,即其模数应大于负极点的模数[32]。考虑到这一点,选择了KPI=0.75的值,从而得到主导的闭环极点pMPI=0.75。
类似地,图5显示了系统矩阵MPID的三个极点的模数随KPID的变化情况。当KPID=0.056时,系统主导极点的模数最小,即min(| pMPID|)=0.56。在此增益下,负极点的模数更小,从而使其不利影响最小化。
最后,为了进行比较,还测试了P控制器,其值取为K P =0.5,该值在系统稳定裕度范围内选取,作为中间值。因此,它将闭环极点置于pMP =–0.5。
总之,表I 包含了所有选定的控制器增益值以及相应的系统主导极点。
表I 每个控制器的增益和系统主导极点
| 控制器 | Gain | 主导极点 |
|---|---|---|
| P | KP=0.5 | pMP=‐0.5 |
| FRR‐I | KF=2.5 | pMF=0.5 |
| BRR‐I | KB=10 | pMB=0 |
| TR-I | KT=3.43 | pMT=0.41 |
| PI | KPI=0.75 | pMPI=0.75 |
| PID | KPID=0.056 | pMPID=0.56 |
B. 测试用例
系统最初已针对设定点输入的阶跃变化进行了测试。阶跃形设定点表示从某一时刻起,系统功耗需要达到另一个不同的恒定功率值。因此,实验结果展示了在视频解码活动中需要保持恒定功耗时系统的响应行为,例如在不考虑其他能耗或体验质量相关问题的情况下,实现对电池放电速率的调节。在后续实验中,设定点将需要动态调整以满足每一时刻的功耗需求。这些需求主要取决于两个方面:用户期望(如电池充电周期和/或体验质量)以及视频解码器需求(如解码复杂度)。近年来数字视频标准的发展正提出在比特流中集成元数据,用于传递视频解码复杂度信息[35],该信息可用于调节控制系统的设定点。
假设系统工作在其 mid‐OPP(默认状态),这意味着平均功耗估算为 1.059 W。同时假设在某一时刻需要系统降低其功耗。为了便于分析闭环系统响应,目标降低的功耗被设定为与某一 OPP 的平均功耗水平一致。如果目标功耗选择在两个连续 OPP 级别之间,由于非线性量化被控对象输入,控制器的积分作用将在稳态系统响应中产生振荡。因此,本测试将设定点从 1.059 W 下调至 OPP8 的平均功耗水平,即 933 mW,在时间 t=1 s 处进行。这相当于施加一个幅值为 ‐126 mW 的输入阶跃。
C. 结果及其讨论
以下各图(为便于比较,全部集中于下一页)展示了控制系统对测试用例阶跃信号的响应情况。出于验证目的,每张图分别表示某个控制器的仿真结果和实时响应,即图 2和图1所示系统的输出。因此,从图中可以看出,实际系统的功耗遵循了仿真对所有控制器预测的趋势,从而验证了控制系统的实现。另一方面,通过对比各图可以识别不同控制器对系统响应的影响。在这方面,最特殊的情况可能是图6对应的P控制器,因为它是
只有P控制器未能达到期望的最终平均功耗933 mW。这是由于P控制器固有的稳态误差,正如第二节中已提前指出的。此外,由于系统极点为负值(见表I中的PMP),P控制器响应表现出一个采样周期的超调。另外,尽管当| P MP|=0.5时,调节时间可能被认为更长(与FRR‐I或PID情况相当,如表I所示),但由于系统误差(在积分情况下可避免)和类似死区效应的非线性量化被控对象输入的共同作用,系统响应无法达到其线性预期的最终值,从而缩短了瞬态响应。
其余包含积分组件的控制器能够达到期望的最终值,因为它们对阶跃型设定点(式(3)中的ess)具有零稳态误差。因此,它们的时间响应差异仅限于暂态部分。在这方面,BRR‐I控制器对应的情况尤为有趣,因为它在系统响应中产生了最短的调节时间,即仅一个采样间隔,如图7所示。这是由于该控制器对应的系统极点的模数最小,即p MB=0(见表I)。
TR‐I控制器将系统的两个极点置于z=0.41(见PMT在表I中),并导致系统响应如图8所示。在这种情况下,阶跃响应的调节时间为500毫秒,并且沿着该区间内的5个采样点单调趋近于最终值,这符合正实数极点的特性。
相应地,FRR‐I控制器将两个系统极点置于z=0.5(参见
对于这两个组合控制器,比例积分控制器将主导系统极点置于z=0.75。由于其模数最大(见
最后,将系统主导二重极点设为z=0.56的PID组合(见pMPID 中的表I),其调节时间与FRR‐I控制器相似,约为pMF =0.5(见图11)。与FRR‐I控制器的情况类似,其时间响应表现出两样本输入输出延迟,即需要200毫秒才能对输入阶跃做出响应。在这种情况下,原因仅仅是被控对象输入处的量化过程。

VI. 结论
本文提出使用闭环控制系统来调节多媒体移动设备的功耗。在环路的前向部分,采用常见的动态电压频率调节机制作用于功耗;而在反馈部分,则提出一种基于电源管理控制器的功耗估计方法,以避免需要专用的功率/能量传感器。已获得一个线性系统模型,并基于该模型设计了一组经典线性控制器,以检验其对系统行为的影响。该简化模型具有足够的通用性,可适用于大多数常见的多媒体移动平台。此外,采用一款商用低成本开源软件应用平台,实现了视频解码器和针对所设计控制器的功率控制系统。同时,还使用包含基于OPP的非线性DVFS接口的仿真器对控制系统进行了验证。系统测试时设定一个导致解码器功耗突然降低的设定点,即负输入阶跃。
结果表明,一方面,实际系统功耗与仿真响应相吻合。另一方面,系统在所有情况下均保持稳定,并能够在稳态下跟踪设定点,其中基于积分的控制器明显优于最简单的 P控制器。此外,组合的PI和PID控制器并未比某些更简单的积分控制器取得更好的效果。事实上,BRR‐I控制器实现了最快的响应,调节时间仅有一个采样间隔。然而,由于DVFS的非线性特性,当没有OPP能够消除环路误差时,这种高响应性可能会导致不希望出现的频繁振荡。因此,TR‐I控制器可能在调节时间和响应性之间实现了最佳折衷,产生平滑且足够快速的响应。这些结果,加上控制系统所隐含的低开销,验证了其作为一种使系统功耗保持在期望值(设定点)附近的方法的有效性,无论视频解码器的动态功耗需求如何。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








