移动无线传感器网络最优监测

原创于 2025-10-30 04:18:08 发布 · 959 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#移动传感器 #最优监测 #事件定位 #感知模型 #通信协议

使用移动无线传感器网络实现基于流量系统的最优监测

1. 引言

基于流的系统（FBS）是一类物理系统，例如供水系统（WDS）、油气管道和人体心血管系统，可被建模为流网络，其中流体（如水、油或血液）在网络的边上流动。这类系统容易受到可能带来严重健康和经济影响的事件的影响。例如，人体循环系统中动脉阻塞是一个需要在早期阶段识别的关键问题，以避免心脏病发作的风险；而在供水系统（WDS）中及早检测泄漏对于避免损失是必要的。

示意图0

尽管对FBS进行连续监测对于长期维护至关重要，但在有需要时对FBS进行按需监测也同样重要，例如当怀疑WDS中存在事件（即血管堵塞或水管泄漏）时。必须有一种机制能够以一定的精度识别事件的存在与位置，以便采取相应的纠正措施。

现有的FBS监测机制效率低下且成本高昂。例如，供水管网监测传统上是通过在关键位置部署静态传感器来实现的。静态传感器通常价格昂贵，并且由于传感器分布稀疏，而供水管网通常规模大且结构复杂，因此难以有效覆盖整个供水管网。因此，在保证事件检测的低误报率和漏报率以及精确定位事件的前提下，使用最少的监测基础设施来监测此类系统变得至关重要。我们将此称为optimal monitoring的FBS。近年来纳米技术与无线传感器网络（WSNs）的发展，使得利用移动设备设计FBS监测系统成为可能。因此，移动传感器可在管道网络中移动（例如在输水管道中）已相继提出。然而，大多数先前的解决方案并未以优化FBS监测为目标。

直到最近，利用移动传感器进行最优FBS监测的研究才受到关注。在Suresh等人[2013]中，作者提出了一种在无环流网络（如WDS）中使用移动传感器和静态信标进行事件检测与定位的初步解决方案。移动传感器在选定位置（例如存在检查井的位置）被注入到无环流网络中。信标是战略性布置的静态设备，用于移动传感器的定位。传感器由FBS中流体的流动推动，在遍历边的过程中检测事件。作者证明了无环流网络的最优监测问题是一个NP难问题。Suresh等人[2013]考虑了一种简化的二元感知模型，该模型为确保事件检测中的最大漏报率（由用户设定）所需传感器数量带来了较高的成本。由于传感器与信标之间缺乏通信，Suresh等人[2013]还要求对传感器进行物理回收。

在本文中，我们设计了一个完整的FBS监测架构，包括用于最优事件检测与定位的算法，以及传感器之间和传感器与信标之间的通信机制。我们还建模了更复杂的感知能力，以解决当前解决方案[Suresh et al. 2013]的局限性。我们提出的主要思想是通过利用传感器和信标的感知与通信能力来降低监测成本。该设计引发了一系列有趣的科研问题。在具有高传播延迟的环境中（例如使用声学通信的供水管网WDS），传感器间通信可能会产生大量碰撞。此外，节点移动的随机性可能导致传感器间通信效率显著降低。我们旨在解决的第一个研究问题是设计一种MAC协议和组管理协议，以最大化传感器之间的通信效益。此外，Suresh et al.[2013]仅关注在哪里以及部署多少个传感器。然而，我们可以利用传感器间通信来辅助事件定位。因此，本文还考虑了何时插入传感器，以确保穿越不同路径的传感器之间存在充分的传感器间通信。我们探讨了新的感知与通信模型如何影响FBS监测算法（即传感器与信标部署）。最后，我们将各种解决方案封装成一个用于FBS监测的集成架构。

该FBS监测的集成解决方案包含感知模型、通信模型、传感器节点的组管理协议，以及基础设施部署算法，从而满足用户需求（例如，事件检测的最大漏报率和最大事件定位误差）。

本文的贡献如下：
- 我们提出了首个用于使用移动无线传感器网络监控FBS的集成架构。
- 我们扩展并提出了适用于FBS的感知与通信模型，并提出了首个用于FBS监测的组管理协议。
- 我们设计了算法，以解决使用具备通信和更复杂的感知能力的传感器监控FBS的问题。
- 我们通过概念验证系统实现和测试平台评估，证明了我们方案的可行性。我们通过大规模仿真展示了其在大型网络中的高效性。

本文的其余部分结构如下。我们在第2节中提供了一些必要的背景知识，并对模型和问题进行了形式化描述。在第3节中，我们描述了传感器和信标的功能，以及用于最优FBS监控的算法。我们在第4节中展示了测试平台评估。第5节展示了在我们的仿真器中进行的大规模仿真的结果。我们在第6节中讨论了该领域的研究现状。最后在第7节中进行总结。

2. 背景与问题表述

在本节中，我们提供本文所考虑问题的一些背景知识和问题描述。为了帮助理解所使用的术语，我们在表I中列出并定义了相关符号。

2.1. 背景

在本文中，我们研究了使用移动传感器和静态信标对标注为 F的FBS进行最优监控的问题，其中最优性指的是监测成本的最小化，即使用设备的数量。通常，我们关注的是监控某个特定区域（或边的子集） F。我们将这样的区域称为感兴趣区域I。当效用管理者怀疑某个区域受到威胁，或患者的诊断表明某个器官存在潜在威胁时，便会部署移动传感器[Suresh et al. 2013]。回收这些传感器通常既昂贵又耗时。

监控FBS涉及识别事件的存在和位置。在可容忍定位误差LE和漏报率FN有界的情况下，我们通过减少使用设备的数量来优化监测成本。

我们将定位误差LE定义为事件被怀疑存在区域的半径。当确定FBS中存在事件时，我们需要确定该事件的位置，以便及时处理。需要说明的是，定位误差并不指实际事件的影响范围，而仅指定位的分辨率。

FN是指在图结构 I 的某条边上存在的事件未被检测到的概率。通过任何监测机制，无论是由于传感器的质量问题，还是因为事件发生区域未被感知，都可能导致事件的存在未被检测到。

FBS中的流，例如供水系统中的流，其大小和方向可能随时间变化。然而，在任何特定时刻，FBS中的流都可以表示为有向无环图DAG。本文假设在某个时间段内，FBS监测期间FBS中的流保持不变。因此，针对本文所考虑的按需FBS监测，FBS可被表示为有向无环图DAG。

从数学上讲， F是一个无环流网络（即有向无环图DAG或网络）G(V,E)。V是FBS中的顶点集（例如供水管网WDS中两根管道连接的管道 junction），而E是FBS中的边集（例如供水管网WDS中的管道）。有向无环图DAG G中的每条有向边(u v)都有容量和流量。流入任意顶点的总流量等于该顶点的流出量。此外，管道中的流量受管道容量的限制。

如前所述，在一天中的某些时段， F中的流量不发生变化。

FBS的一个重要特征是传感器的移动性。传感器由于FBS中基础流体的流动而发生移动。

考虑FBS F，其中 F顶点处的流分布已知。传感器沿特定边（例如，WDS中的管道）的流向移动。当传感器到达一个顶点（例如，WDS中管道的连接点）时，根据系统中的流分布以及流体的物理特性，传感器所选择的下一条遍历边遵循一定的概率分布。当FBS的流分布和物理动态已知时，我们确定在某一顶点选择某条出边的概率与该出边的流分布成正比。

我们将这些概率汇总到一个矩阵M中：
$$
M= \begin{pmatrix}
0 & p_{12} & … & p_{1(|V|)} \
p_{21} & 0 & … & p_{2(|V|)} \
… & … & … & … \
p_{(|V|)1} & p_{(|V|)2} & … & 0
\end{pmatrix},
$$
其中 $|V|$ 是 F中顶点集V的总数，$p_{ij}$表示位于顶点$v_i$的传感器遍历边$e_k$到达顶点 $v_j$的概率。

我们在FBS的算法中利用了该概率分布的知识。

Suresh 等人[2013]提出了无环流网络中的最优事件检测和最优事件定位问题。这两个问题的形式化定义如下： —最优事件检测问题：给定一个无环流网络 F，感兴趣区域I中的 F，以及覆盖度Dc，求插入点集合S={(si,qi) | si ∈V,qi ∈ N}（源点），即需要部署传感器的位置si，以及在每个si处需部署的传感器数量qi，使得其感知路径对I中每条边的覆盖概率大于或等于Dc，并使部署的传感器总数∑ |S| i=1 qi最小。 —最优事件定位问题：给定一个无环流网络 F，感兴趣区域I中的 F，以及事件定位所需的精度Pd，计算需要在 F中部署的最少信标数量及其部署位置（即，顶点集V中的顶点，使得事件定位的概率为Pd。通过识别事件可能存在的边集（即可疑列表），使用所有部署在F中的传感器的路径摘要PS{i}{j}{q}（一组路径摘要）来定位事件X。

2.2. 最优监控问题建模

Suresh 等人[2013]通过从集合覆盖问题的归约证明了最优无环流网络监控问题是NP难问题，并提出了一个具有 ln |V| 近似比的贪心算法。从问题的建模可以看出，作者未考虑传感器的部署时间。Suresh 等人[2013]还假设传感器不具备通信能力，且传感器采用基本的二元感知模型，即只有当传感器穿过包含事件的边时才能检测到该事件。

在本文中，我们将最优FBS监控问题分解为两个子问题来解决：传感器部署和信标放置。

给定感兴趣区域I在 F中、可容忍的定位误差LE,以及漏报率的上界FN，我们需要找到以下内容：
(1) 传感器部署（位置和时间） S={(si,qi, ti) | si ∈顶点集V,qi ∈ N, ti ∈ N}，其中qi表示在时间ti于顶点si 插入的传感器数量，以及 (2) 信标放置 B={Bi | Bi ∈顶点集V}，其中Bi表示放置在顶点 vi,的信标
使得出现在图结构 I 中任意边上的事件 X 的定位误差小于 LE，事件检测的漏报率小于 FN，并且最小化传感器数量和信标（即 ∑|S| =0lii 和 |B|）的数量。

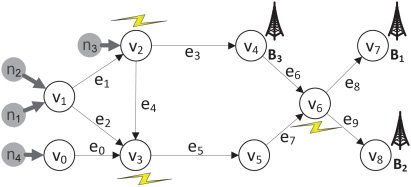
示例：为了更好地理解这些概念，请考虑图2中的 F，其中每条边为50米。闪电符号表示网络中传感器沿不同路径可能通信的位置。我们WDS监控系统的用户指定以下条件：感兴趣区域I包含 F中的所有边，最大事件定位误差LE为50米，最大漏报率FN为20%。FBS的最优监测问题因此涉及传感器部署（即部署位置与时间）和信标放置的决策。图中显示了一个可能的解决方案。

在解决 F的最优监测问题之前，我们需要明确传感器和信标的功能。从高层来看，传感器能够识别事件，并将这些事件报告给其他传感器和信标，而信标则广播其ID，并具备从传感器收集数据的能力。除此之外，我们的解决方案还需要一个明确的架构，以及针对传感器和信标节点的感知与通信能力的形式化模型。这些内容将在算法设计、仿真以及对我们所提出系统的全面理解中发挥重要作用。

示意图1

3. 用于FBS监测的移动无线传感器网络：架构、模型、协议和算法

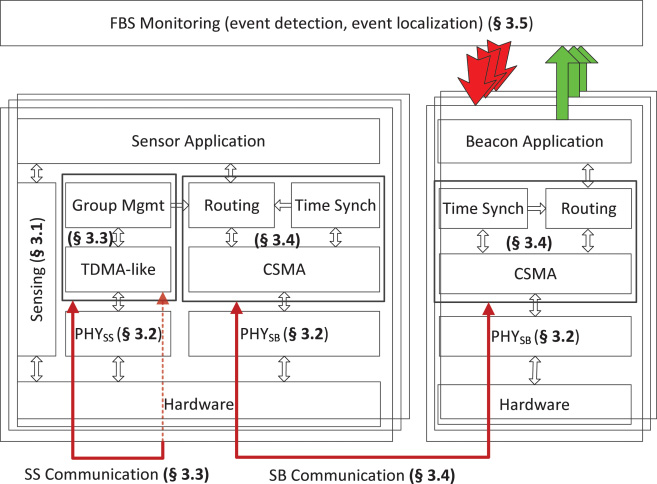
我们提出的用于FBS监测的移动传感器网络架构如图3所示。FBS监测组件确定传感器和信标的布置。移动传感器节点（运行所示的传感器应用）感知环境，并通过PHYSS（例如供水管网中的声学调制解调器）相互通信。传感器节点能够通过PHYSB（例如供水管网中的射频）与 strategically 布置在管道外部的静态信标进行通信。这些静态信标协助移动传感器实现时间同步并收集数据（信标应用）。信标收集的数据由FBS监测组件处理，以实现事件定位。

我们现在详细描述该架构的各个组成部分，即感知模型、物理层模型（以供水管网 WDS为例）、传感器‐传感器通信协议（即基于类时分多址协议的组通信）、传感器‐信标通信协议（即基于载波侦听多路访问CSMA的路由和时间同步），以及FBS监测的算法（即传感器与信标部署和事件定位）。

3.1. 感知模型

传感器的设计取决于需要感知的事件以及FBS的物理特性。然而，为了在我们的最优FBS监控算法中使用，有必要将感知过程建模为数学模型。在本节中，我们为FBS中的任何一般性事件设计了一个感知模型。

为了对FBS中的感知进行建模（如图3所示），我们考虑两种不同类型的事件：非扩散性和扩散性。Nondiffusive事件主要基于距离[Aitsaadi et al. 2007]传播（例如泄漏）。Diffusive事件则基于流分布以及通常随时间传播（例如供水管网的化学污染）。

通常，用于监测物理现象的传感器（例如用于检测泄漏和堵塞的压力传感器，以及用于检测化学攻击的化学传感器）具有特定的灵敏度。当事件在检测点处的强度高于传感器灵敏度时，传感器才能检测到该事件。这取决于事件在攻击点处的强度、事件通过流网络到检测点的距离、FBS网络结构以及每条管道中的流量。对这类传感器进行建模非常复杂。

因此，在初步尝试中，我们考虑事件与传感器之间沿网络边的距离，以及是否存在可用于确定特定类型FBS中事件传播的工具，例如供水管网中的污染物传播。

事件在发生处至参考距离rref范围内被传感器感知到的强度称为S(0)。我们定义S(r)为事件通过管道传播到距离r处的强度。每个传感器都有一个灵敏度S；例如，图1(c)所示的普渡大学/ 德州农工大学化学传感器可调节其灵敏度，范围为0.1至10毫克/升[班克斯等 2012；Wu 等 2014]。如果S(r) > S，则该事件被检测到。

3.1.1. 非扩散事件模型

该模型描述了事件在距源一定距离处的强度（如噪声、压力等）。S(r) 在此模型中由
$$
S(r)=\begin{cases}
S(0)\left(\frac{r_{\text{ref}}}{r}\right)^{\alpha} + N(\mu, \sigma^2) & \text{if event is upstream} \
\beta S(0)\left(\frac{r_{\text{ref}}}{r}\right)^{\alpha} + N(\mu, \sigma^2) & \text{if event is downstream},
\end{cases}
$$
其中 α是事件的衰减因子， N是具有均值μ和方差σ²的正态分布噪声。如果事件向上游传播，则 β为1；否则β为0。我们在此指出，rref= 0对应于二元感知，即传感器仅通过遍历存在该事件的边来检测事件。

3.1.2. 扩散性事件模型

该模型描述了事件的扩散特性（例如，由非反应性物质引起的污染）。此类模型的一个示例是EPANET [环境保护局 2006]中使用的水质模型。事件的强度主要由FBS中顶点处的流分流和混合决定。假设事件通过管道时的强度是均匀的。 F中某顶点处事件的混合/分流是来自该顶点输入边的事件强度的流量加权分布。

对于供水管网（WDS）的具体情况，EPANET [环境保护局 2006]模拟了化学污染随时间在供水管网管道中的传播过程。通过使用EPANET，我们获得了关于供水管网边集中化学污染物浓度的报告。化学污染物的浓度随时间变化。扩散事件流入系统与传感器部署之间的时间差（以小时为单位）记为 τ。更具体而言，在本文中，假设在怀疑发生事件后约 τ小时部署传感器。在扩散事件发生 τ小时后，供水管网管道中化学污染物的浓度由 EPANET获得，EPANET根据管道的尺寸、管道内的流、以及其他物理特性（如反应速率，取决于体积、温度和质量）来计算该浓度。

3.1.3. 感知范围矩阵

我们使用所提出的感知模型来定义感知范围的矩阵M
$$
SR(i,j)=\begin{cases}
1 & \text{if } S(r)> S \
0 & \text{otherwise},
\end{cases}
$$
其中r是边ei和ej的中点之间的最小边遍历距离。对于任意边ei，SR矩阵的第i行表示在边ei中的传感器可以感知到的边，而第i列表示其感知范围包含边ei的边。我们注意到，矩阵SR是基于预设的S(0)计算得到的，该值是我们模型设计用于检测事件的最小强度。

我们在此指出，通过适当设置参数，此处提出的感知模型可用于拟合任何感知模式的行为。任何来自衰减模型或稀释模型（在本例中由EPANET建模）的不确定性或偏差均可被建模为噪声。然而，这种拟合只能是一种近似。

在图2所示的示例中，给定传感器和信标节点的硬件能力，假设 α= 1, β= 0, S= 0.0001 毫克/升，S(0) = 0.5毫克/升，且rref= 0.01米。因此，事件可被检测到的距离r为 $(S(0)/S)^{1/\alpha} \cdot r_{\text{ref}} = 50$米。现在，SR(5, 0)、SR(5, 2)和SR(5, 4)均为1（即位于e5的传感器可以感知e0, e2,和e4中的事件），因为通过管道在e5与e0,e2,和e4之间的距离小于50米。然而，由于通过管道在e5与e7之间的距离为50米，因此SR(7, 5)= 1且SR(5, 7)= 0，因为 β= 0。

3.2. 物理层模型（PHYSS和PHYSB）

对于不同的FBS，由于通信介质的不同，所采用的通信机制也可能不同。例如，在WDS监测中，由于传感器位于水下，传感器之间的射频通信并不适用，因此更倾向于使用声学通信。将通信机制纳入一个通用的通信模型有助于将其应用于我们的最优FBS监控算法中。

在本节中，我们设计了传感器‐传感器和传感器‐信标通信的通信模型。

如图3所示，移动传感器可以与其他移动传感器以及信标进行通信（当它们彼此在通信范围内时）。然而，PHYSS和PHYSB物理层的设计取决于FBS监测基础设施部署的物理环境。例如，在供水管网中，移动传感器之间使用声学调制解调器进行通信，因为传感器可以通过管道作为波导进行通信。而传感器与信标之间的通信则采用射频（RF），这是由于水下（即管道内的传感器）与地面（即管道外的信标）之间的声学传输存在局限性[Sun et al. 2011]。在本文中，我们建模了供水管网的一个具体案例，其中PHYSS为水下声学通信，PHYSB为射频通信。

我们将地下水下传感器与放置在管道外的信标之间的射频通信路径损耗建模为对数距离路径损耗模型：
$$
H_{\text{RF}}= PL_{\text{RF}}(r)-PL_{\text{RF}}(r_{\text{ref}})= 10n\log\left[ \frac{r}{r_{\text{ref}}}\right]+ N(\mu, \sigma^2),
$$
其中，r为距离，rref为参考距离（设为1m），n为路径损耗指数，其值取决于源与接收器之间的障碍物。 N是均值为 μ、方差为σ²的正态分布噪声。我们评估了水管中的传感器与外部静态信标之间的射频通信，并在第4节中展示了结果。

我们使用路径损耗模型对声学信号传输进行建模，如下所示：
$$
H_A= PL_A(r)-PL_A(r_{\text{ref}})= 10k\log\left[ \frac{r}{r_{\text{ref}}}\right]+ ar+ N(\mu, \sigma^2),
$$
其中，r为距离，rref为参考距离（设为1m），k为取决于管道结构的因子，a为由所输送流体（即水）决定的因子， N为均值为μ、方差为σ²的正态分布噪声。

我们使用圆柱路径损耗模型 [Urick 1983],对直管中的声学通信进行建模，其中 k = 1 和 a=A+ 1，其中 A 是由于散射引起的损耗。对于带有弯道的管道，我们采用球面扩展模型 [Kokosalakis 等人 2006] 作为近似，其中 k= 2，a 是取决于声波频率的水的吸收系数 [Urick 1983]。

3.2.1. 传感器的通信距离(CRs)

CRs定义为声学发送器与接收器（即传感器）之间的最大距离，在无噪声和干扰的情况下，接收器能够在已知发射功率下解码发送器传输的数据。

3.2.2. 信标的通信范围(CRb)

CRb定义为射频发送器与接收器（即传感器）之间的最大距离，在无噪声和干扰的情况下，接收器能够以已知的发射功率解码发送器传输的数据。

我们使用信标的通信范围矩阵CRb如下所示：
$$
CRb(i,j)=\begin{cases}
1 & \text{if } r< CRb \
0 & \text{otherwise},
\end{cases}
$$
其中 vi ∈V 且 ej ∈E，r 是从 vi 到边 ej 中点的物理距离。对于每个顶点 vi，矩阵 CRb 的第 i 行表示为了能够接收到位于 vi 的信标信号，传感器需要所在的那些边。对于每条边 ej，第 j 列表示与位于边 ej 上的传感器处于通信范围内的顶点。

3.3. 传感器间通信协议

传感器之间的通信具有两个重要作用：（1）作为位置指示器（如无测距定位 [Stoleru et al. 2007] 中所述），从而减少仅为该目的而部署的信标数量；（2）需要通过这些通信来收集传感器信息，这些传感器可能沿着没有信标可报告数据的路径移动。在我们的设计中，传感器节点使用组管理（如图3所示）来减少通信流量。与陆地射频网络不同，水下声学网络存在高传播延迟，这使得在确保低碰撞率的同时降低延迟变得具有挑战性。在本节中，我们设计了用于传感器之间通信的媒体访问控制和组管理协议，该协议具有低碰撞率，并能够确保传感器组以有界延迟交换数据。本节将描述该协议并证明其延迟界限。

在我们的传感器间通信协议中，我们假设节点具有唯一标识符。当一组节点被部署到网络中时，会预先指定一个领导节点。在我们的组管理协议中，每个节点在其距离范围内都有一个领导者，且任意两个领导者彼此不在对方的距离范围内。节点所属的组由其领导者决定。领导者随机选择一个组ID gi，并周期性地广播一种称为GROUP-HELLO的心跳消息，该消息包含节点IDni和组ID gi。组内其他节点不相互之间也不与领导者进行通信（即声学信道）。组内的所有节点（包括领导者）都会感知数据，并存储最近接收到的信标。我们的用于组管理的分布式算法如算法1所示。

领导者之间的声学通信是基于时隙（类似TDMA）的。一个哈希函数将组ID gi映射到一个素数 pi。领导者以周期 pi广播GROUP‐HELLO数据包（第4到第8行）。

当组成员未收到组问候（即从主群中发生子群分裂）或领导者听到另一个领导者的组问候（即两个或更多群组合并）时，会出现复杂情况。接下来将描述这些情况。

算法1：节点ni上的组管理

要求： 节点列表, gi,li
1: 已合并 ← false
2: for每个时隙 Ti do
3: 如果 ni=li 那么
4:   如果 Ti%Prime(gi)= 0 那么 
5:     如果 已合并 = true那么
6:       发送 组合并
7:     else
8:       发送 组问候
9:     结束 如果 
10:  结束 如果
11:  如果 收到来自n的组问候 j then
12:    已合并 ← true;li ← nj; gi ← gj
13:  结束如果
14: else
15:    已合并 ← false
16:    如果 Ti%Prime(gi) = 0 ∧未收到hello消息 则
17:      等待时间= 1
18:    end if
19:    如果 等待时间 =在节点列表中 ni 的排名 则
20:      li ← ni；gi ←新组ID
21:    否则如果 等待时间 > 0则
22:      增加等待时间
23:    结束 if
24:    如果 收到来自 nj ∧nj ≠ li的组问候，则
25:      li ← nj；gi ←组ID nj
26:      等待时间= 0
27:    结束如果 
28:  结束如果
29:  如果收到来自n的组合并 j then
30:    已合并 ← true；更新节点列表
31:  结束如果
32: 结束循环

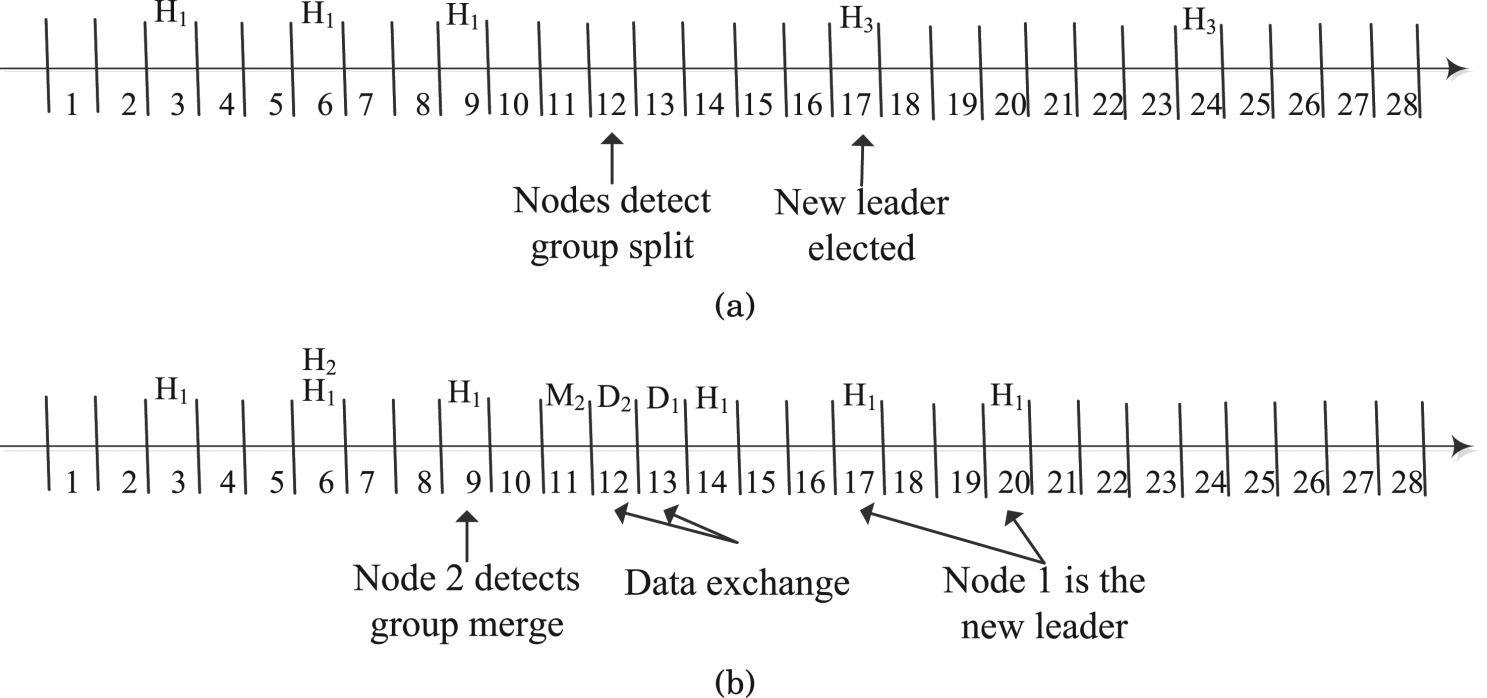
3.3.1 组分裂与领导者选举

当一个组gi split发生时，包含领导者li的子组将继续作为组 gi。在没有领导者的组中，某个节点将根据以下规则决定成为新领导者：在检测到领导者缺失后，每个节点会依据其在组分裂前的节点列表中的排名等待相应的GROUP‐HELLO（第 16至23行）。例如，如果某节点在组分裂前的排名为8，则该节点将等待7个时隙。若未收到任何GROUP‐HELLO数据包，该节点将承担领导者角色，并广播其ID以及一个随机选择的组ID（第20行）。组内所有节点将接受该领导者和组ID，并不再竞争领导者角色。基于新选择的组ID的哈希函数将生成一个新的素数pj。新的领导者将开始以周期pj广播 GROUP‐HELLO数据包。

示意图2

3.3.2. 组合并与领导者选择

当一个领导者 li收到来自另一个领导者lj的GROUP‐HELLO数据包时，这两个组需要进行合并。领导者 li放弃其领导者角色，并接受新的组ID gj和新领导者lj的ID（第11行）。经过 pi个时隙后，li发送一个GROUP‐MERGE数据包，取代 GROUP‐HELLO，其中包含新领导者的IDlj、新的组 gj、组 gi中的节点ID以及组 gi所维护的数据（第6行）。li在此之后将不再通信，除非在组分裂后再次成为领导者。当组 gj的领导者收到来自组 gi的领导者发送的GROUP‐MERGE数据包时，它会响应其组内节点的ID（即组 gj）以及组 gj所维护的数据（第6行和第30行）。

3.3.3. 组管理的延迟分析

在MAC层，我们将时隙大小设置为使得一个节点发送的消息能够在一时隙内到达通信范围内的所有节点（例如，如果通信范围是10米，则选择的时隙为7毫秒）。这样做是为了避免与水下声学通信相关的时空不确定性[Ma和Lou 2011]。由于节点仅在为素数倍数的时隙中传输，因此识别组合并的最坏延迟为kp+ 1，其中k+ 1为合并的组数，p是所有合并组中的最小pi（min(pi)∀合并gii）。由于组gii中非领导者的节点期望每pi个时隙从其领导者接收到一次组问候，因此检测组分裂的时间为pi。

3.4. 传感器‐信标通信协议

传感器与信标之间的通信是必要的，以便在不物理收集传感器的情况下从传感器收集信息。

在本节中，我们设计用于传感器与信标之间通信的协议。

当节点进入信标通信范围时，使用克里斯蒂安算法 [Cristian 1989] 进行时间同步。此步骤是必要的，因为节点需要向信标报告带时间戳的数据。所需的时间同步精度在几十毫秒量级，因为传感器之间的声学通信以及事件检测的定时可以容忍此类误差。传感器使用一种简单的流行路由算法。由于通信是无线的，因此在给定距离内的所有设备都可以接收到广播消息。

信标充当汇聚节点，对数据收集至关重要。它们还会定期通过射频HELLO包广播其标识符以实现定位。只有特定的传感器节点（称为领导者）向信标传输数据。领导者的概念及其所属组在第3.3节中介绍。组领导者与信标之间的射频通信基于载波侦听多路访问。当移动传感器接收到信标发送的射频HELLO包时，首先进行时间同步，然后将数据发送给该信标。在与信标节点完成射频通信后，各节点会删除已传输的数据，并开始记录新感知的数据。

为了节省电力，节点可以使用占空比机制。每次接触时能够传输到信标的总数据容量取决于信标间隔、占空比以及通信范围。必须适当地选择传感器节点在板上的处理量和采样速率，以避免数据丢失。即使采用占空比机制，由于传感器在管道中的移动速度较慢（例如，几米每秒），预计接触时间足以让传感器接收到信标信号。

3.5. 基于流系统的监控算法

我们现在有了用于解决FBS监测问题的工具，即在确保漏报率和定位误差LE有界的情况下，最小化传感器和信标的数量。

3.5.1. 传感器部署：事件检测的部署位置与时间

由于FBS中的流可以在任何时间段内被高精度预测，因此我们可以对传感器布置做出智能决策。当至少有一个已部署的传感器遍历了可以检测到事件的边时，事件检测就会发生。

最优传感器布置问题是指在确保任意一条边未被覆盖的概率高于漏报率FN的前提下，最小化传感器数量的问题。覆盖一条边仅意味着至少有一个传感器遍历该边。因此，我们可以形式化地定义部署传感器数量最小化的问题为
$$
\text{minimize } \sum_{i=1}^{n} q_i
$$
subject to
$$
\left(\sum_{s_i} q_i \ln(1 - ts_{ij})\right) \leq \ln FN \quad \forall v_j
$$
$$
q_i \geq 0 \quad \forall i= 1… n,
$$
其中 tsij= max(tij, tik × SR(j, k)) ∀ ek。tij对每一对顶点而言，表示传感器从顶点vi到达顶点 vj的概率。本节将解释变量和约束。

我们再次指出，前述问题已被证明是NP难问题[Suresh 等人 2013]。因此，本文提出了一种贪心启发式算法。前面提出的模型只能确定在哪里插入传感器以及需要插入多少个传感器。我们还需要确定传感器的部署时间。通过确定部署时间，可以确保传感器组在特定顶点处合并或分裂，从而无需在这些顶点放置信标。传感器布置算法最终决定{si,qi, ti}，其中在时间ti于顶点si插入qi个传感器。

算法2: 传感器部署

要求: 漏报率, F,感知范围
1: {si,qi, 0}=部署位置(F, 感知范围, 漏报率) 
2: {si,qi, ti}=部署时间(F,{si, qi, 0})

算法3: 部署位置

要求: F,SR, FN
1: 对于 每个 ei ∈边集E执行 
2:   对于每个 ej ∈边集E执行
3:     矩阵Mij= P(ej |ei)
4:   end for
5: 结束循环
6: 当 Mk ≠ 0时执行循环
7:   T+=Mk;k++
8: 结束循环
9: 对于 每个 ei ∈E执行 
10:   对于 每个 ej ∈E执行
11:     i′是边集E中ei的终点顶点；j ′是边集E中ej的终点顶点。
12:     ni′j ′= ln(漏报率)/ln(1−Tij) + 1
13:   结束循环 
14: 结束循环
15: for每个 vi ∈顶点集V do 
16:   对于每个 vj ∈顶点集V 执行
17:     Ek= nij个传感器覆盖的 vi和 vj之间的边集
18:     Gij= n ij / (∑_ek ∑_∀el( SR(e k , e l)))，其中 ek ∈边集Ek
19:   结束循环 
20: 结束循环
21: 当圖結構 I 中的边未被覆盖时执行
22:   Gij=min(G)
23:   将 {vi,nij, 0} 添加到 S
24:   更新 G以覆盖边
25: 结束循环

算法2提出了确保漏报率下限的传感器部署（包含其两个步骤）。该算法的步骤1确保了传感器部署的漏报率有界，并在算法3中给出。漏报率下限表示事件存在但未被检测到的概率小于FN。该算法的步骤2确定了传感器的部署时间，并在算法4中给出。

为了确定算法3中的 S，我们首先使用第2节中描述的传感器移动模型。在Suresh等人的研究[2013],中，作者推导出一个表达式，用于计算在某个顶点需要插入的传感器数量，使得至少有一个传感器以大于阈值的概率到达另一个顶点。我们在本文中采用类似的方法。我们利用移动模型中的矩阵M（第1到第5行），并推导出一个转移概率矩阵T（第6到第8行），该矩阵表示传感器从任意顶点到其他任意顶点的转移，其计算基于单步顶点‐顶点转移。
$$
T= M+ M^2+…M^p,
$$
其中Mp+1= 0。集合tij中的元素表示在顶点vi插入的传感器到达顶点 v j 的概率。我们定义teij，即位于顶点 vi的传感器的

算法4：部署时间

要求： F,{si,qi, 0}
1: 初始化J ←空数组，Grev,  ←数组的空数组。
2: IP ←{si}∀si ∈插入点
3: for每个 vi ∈顶点集V 执行 do
4:   如果 inDegree(vi)> 1 ∨ outDegree(vi)> 1则
5:
遍历顶点 vk和 vl之间的边ej，表示为teij= tik×pkl，其中pkl是从vk到 vl的单步转移概率。

我们考虑一个随机变量，该随机变量定义为：当在顶点 vi 部署了 n 个传感器时，遍历边 ej 的传感器数量。位于 vi 的一个传感器以概率 teij 遍历 ej，或以概率 1 −teij 不遍历 ej，这表明该随机变量服从二项分布。因此，当在插入点 vi 插入 n 个传感器时，到达边 ej 的传感器数量为
$$
\binom{n}{x} (te_{ij})^x (1 - te_{ij})^{n-x}, \quad x= 0, 1,..., n,
$$
其中 teij 是从 vi 访问边 ej 的概率。我们希望至少有一个传感器以大于 FN 的概率访问一条边，所需插入的传感器数量将据此确定
$$
(1 - te_{ij})^n \leq FN
$$
for所有边。这表明未访问某条边的概率至多为 FN。此外，
$$
n_{i' j'} = \frac{\ln(FN)}{\ln(1 - t_{ij})},
$$
其中，ni′ j′ 表示为确保至少有一个传感器到达顶点 vi 而需要在该顶点插入的传感器数量。

通过计算所有顶点的 ni′ j′，可得到一个矩阵 N，该矩阵表示在每个顶点需插入的传感器数量，使得至少有一个传感器利用 T 中的转移概率到达另一顶点的概率不超过 FN，（见第 9至14行）。通过确保图结构 I 中的任意一条边未被任何传感器覆盖的概率不超过 FN，即可满足图结构 I 的假阴性率不超过 FN 的要求。

接下来，我们从N推导出一个优度矩阵 G ，以帮助选择最佳的插入顶点和要插入的传感器数量（即 S）。最优顶点的选择是NP难问题 [Suresh等 2013]。因此，我们采用贪心启发式算法来解决此问题（近似比为 ln \|V \| [Suresh等 2013]）。优度矩阵 G定义为 Gij= nij / (∑_ek ∑_∀el(SR(ek,el)))，其中 ek ∈边集 E中连接 vi和 vj被nij个传感器覆盖的，且nij是矩阵N中的一个元素。该表达式的分母表示在 vi处插入的nij个传感器能够感知的边的数量。集合Ek（第17行）是通过从v1开始进行广度优先搜索，并仅搜索所需传感器少于nij的分支计算得到的。

最小的Gij对应最佳插入点，我们将(vi,nij,0)添加到 S（第15到20行）。一旦做出选择，就通过移除每一步中被覆盖的所有边来更新Gij，即移除满足SR(ek,el) = 1的边el，其中e k ∈ Ek（第21到25行）。如果SR较高，则每一步会移除更多的边。

我们将感知覆盖率定义为图结构I中至少被一个传感器覆盖的边的比例。1 ‐ 漏报率的期望值等于期望的感知覆盖率。因此，如果某个传感器部署的感知覆盖率至少为1 ‐ 漏报率，则该传感器部署也满足误报下限要求。我们在传感器部署的评估中使用感知覆盖率作为指标。

传感器到达顶点后遍历的下一条边由该顶点的出流率决定。由于管道尺寸的不规则性以及汇聚节点需求的变化，用传感器覆盖感兴趣区域的难度可能有所不同。因此，我们定义感兴趣区域的不良度为BI= √∑(f i x −fx)² × 1,000，其中fx是感兴趣区域内边x中的流量，而f i x是该边中的理想流量[Suresh et al. 2013]（即所有出流在所有顶点处均等分配，这种情况是理想的，因为它在满足所需漏报率的情况下要求最少的传感器数量FN）。

该算法的一个相关问题是，插入点可能被限制在图结构 I 中的少数节点上（例如，检查井仅在供水管网中的少数顶点处可用）。通过重构图可以克服这一挑战：移除无法到达的顶点，并添加边以保持连通性。

S中传感器的部署时间在算法4中给出。我们将I中具有多个流入/流出边的顶点定义为交叉点J （第3到8行）。这些是沿不同路径行进的传感器可以通信的顶点。此处需要说明的是，经过交叉点的传感器可能通过不同路径移动。我们为I的每条边分配一个权重，该权重等于传感器在该边上所花费的时间，并确定插入点与交叉点之间的最长路径。

设 G(V, E) 和 Grev(V, E′) 为两个有向无环图，其中 G 与 Grev之间的唯一区别是它们边的方向。更准确地说，G 和 Grev具有相同的顶点集，且对于任意 u v，(u ∈) vE 当且仅当 ( ∈, u) ′ ∀ E v ∈，其中 urev ∈ V。从交叉点以广度优先方式遍历 G −，可得到来自不同路径的插入点。若一个传感器需要在时间 t 到达某个交叉点，则它必须在时间 t ′ ti于插入点 s′被插入，其中 ti表示从 sv0到达该交叉点所需的时间。我们针对每个插入点，根据其对应的各个交叉点及通往这些交叉点的路径，获得一组可能的插入时间，如第10至15行所示。

例如，在图2中，若需在时间 t 到达 v1的传感器分别从 v6和 i插入，且任意边 ei的遍历时间为 t v0，则在 0处的可能插入时间为 {t‐t5‐t7‐t v1}，而在 1处的可能插入时间为 {t‐t3‐t6, ‐ t1, t‐t4‐t5‐t7‐t{v34}}。最后，我们在各个可能的插入时间之间均匀分配传感器（第16至21行）。

#### 3.5.2. 事件定位信标放置

信标对于从传感器收集信息以及辅助定位至关重要。然而，在 FBS中处处部署信标成本高昂且效率低下。在本节中，我们描述了一种算法，用于在给定期望的定位误差LE时确定信标的最优放置。

**算法5: 信标放置**

要求：LE,圖結構 I, CRb,SR, J
1: 初始化 pid ← 0, pathsOn, pathSummary, Q←源点 ∈圖結構 I
2: forall s ∈源点 do
3: pathsOn(s) ← pid; pid++; s.φ= 0
4: 结束循环
5: 当 Q不为空时执行
6: vi ←出队(Q)
7: 对于每条路径 ∈pathsOn(vi)执行
8: pathSummary(路径).追加(vi)
9: 结束循环
10: 如果 vi.子节点为空那么
11: 在 vi处放置信标
12: 结束如果
13: 对于每个 vj ∈ vi.子节点执行
14: 如果 vj是 vi的第一个子节点则
15: pathsOn(vj).append(pathsOn(vi))
16: else
17: 对于路径 ∈pathsOn(vi)执行
18: pathsOn(vj).append(pid)
19: pathSummary(pid) ←pathSummary(路径); pid++
20: 结束 for 循环
21: 结束如果
22: vj.φ ← vj.φ+ vi.φ+∑k∑l SR(ek,el)，其中ek ∈为以 vj为终端顶点的边 el使得 CRb(vj,el) = 1
23: 如果 ¬vj.queued 那么
24: Q.enque(vj)
25: 否则如果 vj.φ ≥LE∧ vj∈/J 那么
26: 在 vj处放置信标
27: 结束如果
28: 结束for循环
29: 结束while循环


算法5确定信标放置，以确保在感兴趣区域I（即 F的子图）中定位误差LE有界。首先，我们为顶点 vi定义一个变量vi.φ，用于确定从源点到达 vi的传感器的定位误差。我们通过放置信标来减少所有顶点处的 φ，从而确保LE有界。vi.φ通过算法5进行更新。该算法在第 1到第4行中初始化所需的数据结构。Sources指I中的源点顶点（即入度为1）。我们对图执行广度优先搜索，按拓扑顺序将顶点加入队列，以便确定从源点到汇聚节点的所有路径。

在遍历这些路径时，当 φ超过LE时，我们放置信标。在此算法中，我们跟踪I中从插入点到汇聚节点以及通向感兴趣区域外的边的每条路径。每条路径被分配一个ID。每个顶点vi所参与的路径列表保存在一个映射pathsOn中。每条路径中包含的边列表保存在一个称为路径摘要的映射pathSummary中。

在第5到29行中对图进行了广度优先搜索。在BFS的每一次迭代中，包含该顶点的所有路径的路径摘要将被更新（第7到9行）。由于信标不仅是标识符，还是来自传感器信息的收集点，因此我们需要在所有汇点处放置信标。如果该顶点没有子节点（即汇点），我们在此处放置一个信标以进行数据收集（第11行）。如果一个顶点没有出边指向图结构I，则被视为伪汇点。由于该算法的输入是图结构I，这类顶点没有子节点。如果一个顶点只有一个子节点，则该子节点将被添加到包含父节点的所有路径的pathSummary中。

**算法6: 事件定位**

要求: d, F, CRb, SR, B, PS
1: for每个 PSi在 PS do
2: for每个 EL在 PSi do
3: 如果 X ∈EL 那么
4: 如果 Bi ∈EL，其中 Bi ∈B则
5: 对于所有 ek，满足 (CRb(Bi,ek) = 1) 执行
6: 对所有ej执行
7: 如果 SR(ej,ek)= 1 那么
8: EE.append(ek)
9: ek被标记为可疑
10: 结束如果
11: 结束循环
12: 结束循环
13: else
14: 对于所有 ek ∈边 ei P与N之间的
15: 对于所有ej执行
16: 如果 SR(ej,ek)= 1则
17: EE.append(ek)
18: ek标记为可疑
19: 结束如果
20: 结束对于
21: 结束对于
22: 结束如果
23: else
24: 对于所有 ek使得 (CRb(Bi,ek) = 1) 执行
25: 对于所有ej执行
26: 如果 SR(ej,ek)= 1那么
27: ek标记为已感知
28: 结束如果
29: 结束循环
30: 结束循环
31: 结束条件判断
32: 结束循环
33: 结束循环
34: EE.移除(边 ∈已感知; ∈/可疑)
```

顶点（第15行）。不添加新路径。如果该顶点有多个子节点，则每个子顶点位于不同的路径中。多条路径的路径摘要将在第17至20行中更新。每个子顶点的 φ在第22行中更新。如果某个子顶点尚未入队，则在第24行中将其加入BFS队列。如果该顶点的 φ超过LE（即vi.φ ≥ LE），则在子顶点处放置一个信标（第26行）。此步骤还会更新该顶点作为信标的潜力。

仅当 φ> LE时，我们才在顶点处放置信标。由于顶点是按照拓扑顺序考虑的，因此在每次迭代中，只要拓扑顺序仍然成立，子图中的最优信标放置（不包括汇聚节点）在添加新顶点后仍保持最优。因此，当算法终止时，最优信标放置完成。

3.5.3. 事件定位算法

一旦传感器的数据在信标处被收集，就需要解析这些数据以获取有关事件的信息。在本节中，我们设计了一种算法，利用FBS中的流、信标位置以及从传感器收集的数据来推断事件的位置。

事件的定位（如算法6所示）基于在信标处收集的数据。信标从传感器处收集所遇到的事件和信标的摘要（即路径概要PS）。该事件定位算法推导出列表可能包含事件的边（标记为EE的列表）以确定定位误差。所获得的定位误差是覆盖边 EE中点的圆的半径。

我们根据时间戳将信标收集的路径摘要分类到一个列表中，EL（第1和第2行）。EL是具有相同时间戳的记录数据集合。如果EL同时包含一个事件和一个信标（第3和第4行），则从该信标的CRb中所有边对应的SR的列向EE添加边，并将这些边标记为可疑（第5至12行）。如果EL包含事件但不包含信标，则在上一次观测到的信标P与下一次观测到的信标N之间的路径上的边被认为可能包含该事件（第14至21行）。如果EL中没有事件存在，则将SR中的边标记为已感知（第24至30行）。在遍历所有传感器的数据后，我们从EE中移除那些未被标识为可疑但已被已感知的边（第34行）。

示例：在图2的示例中，传感器经过的路径为 n1: v1 v2v4 v6 v7；n2: v1 v3 v5 v6 v8；n3: v2 v3 v5 v6 v7；以及 n4: v0 v3 v5 v6 v7。如果边 e2上存在一个事件X，并且传感器 n1, 、n2,和 n4同时到达 v6 ，则 n1, 、n2, 、n3,和 n4将分别报告以下信息：(n3,t(n1)1) (B3, t(n1)2) (n2,t(n1)3) (n4, t(n1)3) (B1, t(n1)4)，(X,t(n2)1) (n4, t(n2)2) (X, t(n2)2) (n1, t(n2)2) (B2, t(n2)3)，(n1, t(n3)1) (X, t(n3)2) (B1, t(n3)3)，以及 (n2, t(n4)1) (X, t(n4)1) (n2, t(n4)2) (n1, t(n4) 2) (B1, t(n4)3)，其中 t(ni)j表示节点 ni记录第 j th次报告的时间。根据遍历每条路径的预期时间知识，我们可以定位边 e2上的事件。定位误差LE为 |e|/2= 50m。

4. 概念验证系统实现与验证

我们将利用移动无线传感器网络进行FBS监测的提议通过概念验证系统实现变为现实，该系统包括管道内的移动传感器节点和管道外的静态信标。我们通过将传感器放置在供水管网的管道内、信标放置在管道外来评估传感器‐信标通信，如图5(a)所示。我们还展示了一个使用气流推动传感器的试验平台，如图5(b)所示，以演示感知覆盖率和事件定位能力。

4.1. 验证通信模型的实验结果

我们通过如图5(a)所示的试验平台验证了通信模型。我们在直径分别为 4′′, 6′′, 8′′,和 10′′的四根管道上测试了接收信号强度指示（RSSI）。实验中使用六个配备CC2420射频收发器并由Rayovac AAA 电池供电的传感器，包括信标和传感器节点。其中五个传感器以0.3米的间隔固定在管道外侧，浸入水中的传感器与最下方的外部传感器处于同一水平位置。水中的传感器每次实验在5分钟内广播 3000个数据包。

每根管道的平均、最大和最小接收信号强度如图6(a)至(c)所示。所有管道的接收信号强度指示均随距离呈现对数衰减。尽管接收信号强度指示值变化较大，但在所有实验中均处于–50dbm到10dbm范围内，可保证可靠通信。

从图6(d)可以看出，我们的对数距离路径损耗模型能够很好地拟合实验数据。f(x)线拟合了 4′′和 6′′管道的接收信号强度指示，g(x)则拟合了 8′′和 10′′管道的接收信号强度指示。如我们所见，路径损耗指数为2.9和3.5。需要指出的是，由于我们在管道周围没有使用土壤，实际供水管网部署中的路径损耗可能会更高。因此，正如前面提到的，在我们的理论模型中，我们将路径损耗设为4。任何不准确之处只会导致较低的CRb。

4.2. 概念验证实验平台

对于移动传感器和信标，我们使用由CR2320纽扣电池供电的TI eZ430‐RF2500节点。传感器的组件如图5(b)所示。TI eZ430和

示意图3 用于验证传感器与信标之间通信范围的试验平台。(b) 用于系统评估及传感器节点的试验平台)

电池可以轻松放入一个3.8厘米直径的高尔夫球中。将节点和电池放入用海绵填充的高尔夫球内，可在管道中顺利滚动。为了产生网络流，我们使用工业吸尘器。信标是一个连接到笔记本电脑的TI eZ430‐RF2500 节点。

传感器节点和信标使用C语言编程，其功能如第3节所述并在图3中展示。由于我们的试验平台设计（即没有声学通信），我们仅采用传感器与信标之间的通信，该通信为2.4吉赫兹频段的射频通信。如第3节所述，信标周期性地广播包含其ID和时间信息的射频 HELLO包，以实现与传感器节点的时间同步。当传感器节点接收到信标发送的射频 HELLO包后，会广播采集的数据。即使没有数据上报，传感器也会向信标发送HELLO消息。事件通过使用motes周期性地广播射频信号来模拟。在我们的感知模型中，rref，如第 3.1节所述，为0米。

在MAC层，我们使用IEEE标准802.15.4协议。节点随机退避，在退避结束时，如果连续两次空闲信道评估表明信道空闲，则该节点发送数据。在我们的实验中，我们注意到电池寿命相对较短（∼10分钟，这是由于CR2320电池容量降低所致）。因此，我们采用占空比为10%的低功耗监听（LPL）来延长电池寿命至大约30分钟。TI ez430‐rf2500平台具有32KB闪存和1KB内存。我们对信标节点的实现（∼2,600行代码）使用了301B内存和 4954B程序存储，传感器节点实现（∼3,000行代码）使用了610B内存和5530B程序存储。

为了验证我们的传感器部署算法，我们在图5(b)所示的试验平台上进行了四组实验（即场景）。每个场景具有不同的注入和收集点，并且每个场景重复五次，事件放置在所有边上。每次实验共使用了14个传感器。

各场景在五次运行中的平均感知覆盖结果如图7(a)所示。 e1… e12对应供水管网中的12条边。覆盖一条边对应的感知覆盖率为 1/12。该图还显示了每条边在五次运行中的平均感知覆盖率。在场景1、2、3和4中，使用14个传感器时的漏报率分别为14.5%、23.9%、8.4% 和7.5%，这些值是通过估计所有场景中所有边上的流量得到的。场景1和4中的边e3以及场景2和3中的边e8的流量极低，因此在计算感知覆盖率和漏报率时，它们未被包含在感兴趣区域内，分别对应场景1、4和2、3。

为了验证我们的事件定位算法，我们在图5(b)所示试验平台的一个子集上进行了四组实验（即场景）。这四种场景如下所示

示意图4

图7(b)中展示的结果是10次实验的平均值。通过报告数据的时间戳获得的实际定位误差在场景1和2中为0.2米，场景3中为0.64米，场景4中平均为0.5米。我们观察到，当信标通信范围CRb较小时，场景1至3的定位成功率（1 –FN，其中漏报由通信故障导致）低于100%。造成这一现象的因素包括传感器速度（传感器经过信标时未能唤醒）以及管道结构（弯道和不规则通信范围）。在场景4中，由于较高的CRb，所有事件均被成功定位。因此我们得出结论：移动传感器需要具备更高的发射功率，特别是在使用低功耗监听LPL时，以确保通信故障不会导致漏报。

5. 性能评估：大规模仿真

由于在真实世界的FBS或试验平台中评估我们的算法和协议既繁琐又耗时，我们开发了WDSim。WDSim是专门为WDS设计的模拟器，如图9(a)所示。WDSim包含一个网络模型、算法的实现以及一个WDS simulator。WDSim根据包含网络结构和流量的网络模型，模拟传感器在管道中的移动。该网络模型通过使用(1)某城市WDS的模型生成

示意图5 WDSim框图。(b)带有感兴趣区域I1, I2,和I3的微城市)

（例如，我们使用Micropolis [Brumbelow等 2007]），以及（2）在一天中特定时间网络末端的流量、流速和需求（例如，来自EPANET [环境保护局 2006]的报告文件）。WDSim实现了感知和通信模型（第3.1、3.2和3.4节）、组管理协议（第3.3节）以及所有用于FBS监测的提出算法（第3.5节）。

我们总共模拟了3600个场景，每个场景重复30次，每次使用不同的随机种子值，模拟持续时间为1小时。我们的模拟结果绘制了平均值以及一个标准差（必要时）。为了与研究现状进行比较，我们选择了FlowSim[Suresh等人的方法 2013]。

用于评估我们所提出算法的指标包括：（1）组通信期间的碰撞率以及错过的通信机会百分比（算法1）；（2）传感器数量和感知覆盖率（算法3）；（3）平均值CG（为评估算法4，我们将CG定义为传感器之间组合并次数与可能的总组合并次数的比率）；（4）信标数量以及实现的定位误差（算法5和6）。我们变化的参数包括：（1）CRs，（2）CRb，（3）SR 和感知模型，（4）FN，（5）LE，以及（6）感兴趣区域I。我们考虑了三个感兴趣区域，即I1,、I2,和I3,，如图9(b)所示。图中还展示了这些感兴趣区域的大小和不良度。I1的对角线长度为701米，I2的对角线长度为1349米，I3的对角线长度为1100米。

为了评估感知范围对非扩散事件中算法的影响，我们使用一个参数SR，即在无噪声情况下（即r满足S(r)> S的条件下）能够感知的最大距离=（S(0)/S ）^(1/α) * rref。在我们的仿真中，我们将 S= 10⁻⁴、S(0)= 1、 α= 1、β= 0和rref分别设置为0米、0.001米和0.0025米，从而得到对应的SR分别为0米、10米和25米。组通信算法的评估是在这些场景之一上进行的。

为了评估扩散感知模型，我们假设在事件发生一段时间后插入传感器， τ。本文使用 EPANET的数据，以供水管网管道中污染物的浓度来表示事件的影响范围。当将 τ作为输入提供给EPANET时，它会给出经过 τ小时后每条边中污染物的浓度。我们将τ分别设为 2、4和6小时，同时将传感器的感知阈值S设为1毫克/升、5毫克/升、10毫克/升和20毫克/ 升。这两个参数均会影响传感器的感知范围。

为了选择我们仿真中的CRs ，我们利用路径损耗模型HA推导出相关结果。费舍尔和西蒙斯[1977]推导了声波在海水中的吸收系数，其中纯水引起的吸收表达式定义为A 3 2 − 6.5 × 10⁻¹⁰ 3 2, 3= 3.964 × 10⁻⁴ − 1.146 × 10⁻⁵+ 1.45 × 10⁻⁷ −10 −1 −1 3= 1 − 3.83 × 10⁻⁵+ 4.9 × 10⁻¹⁰ 2, Pf，其中ATTTdBkmKHz；PDD，其中D为水深；f为声波的频率。根据专门为水下声学通信实验开发的试验平台[Ahmed 等人2012],，我们考虑通信频率约为 20千赫。使用第3.2节中的通信模型，对于10千赫、20千赫和100千赫的通信频率，在带弯头和不带弯头的管道中，30米和60米距离的路径损耗HA如图10所示。从图中可以看出，在100千赫时，路径损耗最高。研究人员可根据期望的数据速率和通信距离，利用此分析确定合适的通信频率。这也为我们提供了在评估中使用的合适CRs值。在我们的实验中，我们使用的CRs介于10米到90米之间。

三个感兴趣区域中所有边的中值长度约为10米。我们在感知和通信范围、SR、CRs以及CRb上添加噪声（均值为 μ= 0米，方差为σ²= 1米）。

示意图6 )

5.1. 群組通訊

为了评估算法1，我们考虑了碰撞率以及错过的通信机会的百分比。评估碰撞率很重要，因为碰撞会消耗能量并可能导致信息丢失。为了判断是否错过了通信机会，我们跟踪组合并、组分裂以及与信标的相遇情况。这一点很重要，因为错过的通信机会可能导致假阴性结果。

我们考虑的是针对非扩散性事件场景所推导出的传感器部署。需要注意的是，初始传感器部署仅决定初始网络拓扑结构。

为了评估碰撞率，我们改变了通信范围CRs和节点数量（在FN= 10%、20% 和 30%，以及SR= 10m 的条件下获得）。结果如圖 11(a) 至 (c) 所示。有趣的是，我们观察到增加传感器数量和CRs会导致碰撞增加，但碰撞率始终介于 1.5% 和 4.2% 之间。由于插入的传感器数量以及图结构 I 的不同，不同的感兴趣区域具有不同的碰撞率。

图 11(d) 至 (f) 展示了错过的通信机会百分比的评估结果。我们将算法1与一种时分多工协议进行比较，其中传感器在预定义的时隙中进行广播，同时还与一种假设场景进行比较，即传感器即使发生碰撞也能解码数据包。我们注意到，增加CRs会降低错过的通信机会百分比，因为传感器每次接触时拥有更多的时间。另一个重要观察是，算法1与假设场景之间在错过的通信机会上的差距完全由碰撞引起。

前述评估突显了媒体访问控制和群组管理算法的重要性。同时也强调，拥有足够大的CRs对于确保传感器之间数据传输的可靠性至关重要。

5.2. 感測覆蓋範圍

首先，我们通过改变影响传感器部署的参数来评估传感器部署算法（算法3），这些参数包括漏报率FN、SR以及感兴趣区域。然后，我们通过与其他算法进行比较来评估部署时间算法（算法4）。评估针对扩散事件和非扩散事件分别进行。在扩散事件的情况下， τ也被改变。

对于给定的感兴趣区域，FN和SR，所插入的传感器数量是确定的，并在图12(a)至(c)中表示（即无误差条）。感知覆盖率的评估结果如图12(d)至(f)所示。从图12(a)至(c)可以看出，正如预期的那样，当降低FN时，所需的传感器数量增加。我们还注意到，当SR较高时（即事件可以被检测到）

示意图7 ，I 2(b)和I 3(c)。在I上通过改变CR s = 3 和FN得到的错过的通信机会百分比：FN= 30% (d)，FN= 20% (e)和FN%(f))

从距离污染物源较远的位置开始，确保给定漏报率所需的传感器数量显著减少。在图结构 I3,中，将感知范围从10米增加到25米，可使漏报率= 10%时所需的传感器数量减少91倍，同时感知覆盖率提高1%。尽管预期会有所减少，但值得注意的是其减少的因子。这意味着，在传感器上稍作投入以获得更高的感知范围，可以转化为显著的成本降低。

图12(d) 至 (f) 显示，当漏报率较低时，感知覆盖率有所提升。这是因为我们确保所插入的传感器对每条边的覆盖概率至少为 1 ‐ 漏报率。一个有趣的观察结果是，对于相同的漏报率和感知范围，插入到图结构 I2 中的传感器数量更少，且实现的感知覆盖率高于插入到图结构 I3, 中的传感器数量及其实现的感知覆盖率。

、I2(b)、I3(c)的情况下，为实现漏报率FN所需的传感器数量。在不同漏报率FN、感知范围SR下，在图结构I1(d)、I2(e)、I3(f)中实现的感知覆盖率)

尽管I2中的边数更高。这是因为I2的不良度低于I3。由于I1明显更小，插入的传感器数量少于I2和I3。

在FlowSim [Suresh等人 2013], SR为0米（二元感知）。FlowSim有一个额外的调参参数 α。我们比较了FlowSim中部署的传感器数量和实现的感知覆盖率，分别对应 α= 0和覆盖度 1 −FN，以及WDSim中SR= 0m的情况。FlowSim在I3上的感知覆盖率比WDSim平均少使用17.7%的节点时低45.6%。相反，在I2,上，FlowSim的感知覆盖率比WDSim低8.2%，但平均多使用了166%的节点。这种不规则的差异是由于I2和I3,的不良度不同，导致FlowSim不适用于高不良度的大规模网络。

针对扩散事件，插入的传感器数量及在 τ= 2、4小时和6小时时的感知覆盖率分别如图13、14和15所示。对于较小的 τ，插入的传感器数量较多，因为此时事件尚未在系统中传播开来。非常有趣的是，随着FN的降低，传感器数量减少的趋势并不明显，原因在于与非扩散感知模型不同，事件在系统中的传播并非均匀的。另一个非常有趣的结果是，感知覆盖率上升的趋势也不明显；由于插入的传感器数量较少，单个传感器若未能覆盖任何边，就会导致大量边未被覆盖，因此结果具有较高的方差。这也是当感知阈值S较高时，随着FN的降低，感知覆盖率增加以及节点数量减少的趋势更加明显的原因。

、I2(b)、I3(c)的情况下，达到指定漏报率FN所需的传感器数量。当时间为 τ= 2小时时，在不同漏报率FN、感知范围SR下，图结构I1(d)、I2(e)、I3(f)所实现的感知覆盖率)

我们现在将部署时间算法（算法4）与另外三种算法进行比较：（1）所有传感器同时插入，（2）传感器的部署时间随机选择，（3）传感器分组并周期性插入；其中周期由插入的传感器数量和仿真持续时间决定。我们研究了CRs对本算法的影响。图16展示了非扩散事件的结果，图17展示了扩散事件的结果。此处，FN和SR分别设置为10%和10米。

从图16可以看出，算法4在I1,I2,和I3上的表现优于其他算法。我们观察到，增加CRs会提高CG，因为当通信范围较大时，传感器无需彼此靠近即可进行通信。此次评估清楚地表明了部署时间以及传感器之间通信的重要性。

、I2(b)、I3(c)的情况下，实现漏报率FN所需的传感器数量。当时间为 τ= 4小时，在不同漏报率FN和感知范围SR下，图结构I1(d)、I2(e)、I3(f)所达到的感知覆盖率)

图17显示，除了I3,外，算法4的表现优于其他算法。这是因为传感器数量较少，并且相比非扩散情况，它们集中在更小的区域内。此外，我们观察到可能的接触次数较低。因此，一次通信遗漏就会导致CG大幅下降。正如传感器部署结果所显示的那样，结果的方差较大。