基于活动识别的负荷曲线建模

向居民消费者日常活动的负荷曲线建模

摘要

电力消耗预测是配电企业（DUs）在日常电力供应采购中使用的关键数据之一。由于用电量波动，居民消费者的负荷曲线在各类用户中最为不稳定，这源于每个家庭成员在一天不同时段进行的大量日常和非日常活动。其中，日常活动对用户的日负荷曲线和用电量有显著影响。因此，确定消费者的日常活动有助于配电企业获得更精确的日负荷预测。本文提出一种方法，通过历史电力消耗数据识别消费者的日常活动，并重建其相应的日负荷曲线。该方法通过识别在多个消费者数据中频繁出现的电力消耗曲线来识别可能的日常活动，然后进一步评估特定消费者执行这些活动的概率，以验证每项活动是否确实属于日常活动。基于所确定的日常活动，采用概率方法重建日负荷曲线。由于分析具有概率特性，为每15分钟电力消耗计算了95%置信限，以便配电公司获得可靠的居民消费者日电力需求数据。

关键词 ：需求预测，消费者活动，负荷建模，电力需求

I. 引言

电力消费模式的变化和多样化的生活方式是导致居民消费者电力需求不可预测的原因之一。实际上，配电企业（DUs）的需求预测在其供应采购中至关重要，而这一过程因此变得更具挑战性和不确定性。已有许多文献研究了居民用户负荷预测模型。用电量可通过不同方法在宏观层面[1]和微观层面[2]进行分析，包括统计建模[3]，时间序列分析[4]，以及基于消费者自身行为的分析[5]。这些方法考虑了多种可能影响消费者每日负荷曲线的因素（如天气条件、季节变化、工作日/周末、节假日等），并已证明，除了这些因素外，消费者活动是提高预测精度和准确性的关键因素。居民消费者的活动由日常活动和非日常活动组成。由于非日常活动具有随机性，通常基于消费者的习惯和临时决策，因此难以识别。另一方面，日常活动是大多数消费者每天重复执行的行为，并对每日负荷曲线产生重大影响。本文提出一种方法，用于识别日常活动并重建由这些活动引起的负荷曲线。由于分析具有概率特性，重建的负荷曲线以置信区间形式呈现。对用电数据进行附加的统计分析即可得到置信区间。然而，现有方法识别出特定用电量的原因，即此类活动，因而预测更具实用性。识别非日常活动将是后续研究的另一个步骤。

II. 日常活动的识别

消费者进行的每项活动都会涉及使用某些电器，包括照明和加热设备，并导致一定量的用电量。实际用电量因消费者使用的具体电器而异。该变量应被视为随机变量，而由某项活动引起的用电量具有其概率分布。此分布是该行为的“指纹”。由多项活动引起的总用电量因此是一个随机变量，其分布是这些相关活动分布的混合。我们观察到通过对多个消费者在多个时间段内获得的总用电数据进行方差分析。该方差分析显示了分布混合现象。在混合分布中的某个成员分布越显著，意味着该分布在越多消费者中出现得越频繁，从而推测其对应于一项常见活动。

我们使用在多个家庭中测量的用电量历史数据。电器分为几类，包括厨房电器和娱乐电器，并对每类的用电量进行测量。在时间段U中，由第j项活动a_j（该活动使用了类别m的部分电器）引起的类别m（即m=1{kitchen}, m=2{entertainment}, m=3{household}，…）的单一用途能耗Q_{m,t}，通过条件概率密度函数 f(Q_{m,t}|a_j) 来表示，该函数被定义为混合分布。单一用途能耗因消费者对电器的选择率不同而导致的用电量差异很大。多个活动会使用类别m中的电器，因此该类别的总用电量由所有活动对应的这些条件分布的混合构成。该混合分布的各个成分用于识别各项活动，其参数通过基于期望最大化（EM）算法[6]确定：

$$
\hat{\theta} = \arg\max_{\theta} \sum_{t=1}^{T} \log \left( \sum_{j=1}^{z} P(a_j) f(Q_{m,t}|a_j; \theta_j) \right)
$$

其中，z 是条件概率密度函数的数量，P(Q_{m,t}) 是历史数据的概率密度。

我们假设在进行类似活动时，消费者会使用类似的电器，因此可以认为条件概率密度函数 f(Q_{m,t}|a_j) 在居民消费者之间是通用的。通过这种方式，我们得到了一组以 f(Q_{m,t}|a_j) 表示的活动，这些活动是日常活动的候选者。

接下来，我们使用条件概率密度函数 f(Q_{m,t}|a_j) 来识别特定个体消费者执行的日常活动，该函数表示居民消费者独有的日常活动候选者及其该消费者的历史用电数据。我们使用了前一段中使用的相同函数，但现在我们关注的是该个体消费者的分布。对于此特定个体消费者，我们估计后验概率 P(a_j|Q_{m,t})，用于确定在给定该消费者用电数据的情况下，该消费者执行活动a_j的可能性有多大。

该估计通过应用贝叶斯推断公式的朴素贝叶斯分类器[7]完成：

$$
P(a_j|Q_{m,t}) = \frac{P(a_j) f(Q_{m,t}|a_j)}{\sum_{i=1}^{k} P(a_i) f(Q_{m,t}|a_i)}
$$

其中，f(Q_{m,t}) 是从测量数据中获得的类别m中单一用途能耗的概率密度函数，k 是与电器类别m相关的活动数量。

我们已经获得了 P(a_j)。因此，求解方程 (2) 可得到用于方程 (1) 的先验概率。当某一能耗值的观测次数为n次后，可得到一组包含n个线性方程和k个未知数的方程组。该方程组通过最小二乘法（LSM）进行求解。

我们并不计算方程 (2) 中 P(a_j) 的分布，因为这不会影响分解结果的准确性，因此，我们使用归一化的 P(a_j|Q_{m,t})：

$$
P(a_j|Q_{m,t}) = \frac{f(Q_{m,t}|a_j)}{\sum_{i=1}^{k} f(Q_{m,t}|a_i)}
$$

其中，G(a_j) 是具有 P(a_j|Q_{m,t}) > θ 的时间段的数量。当 S(a_j) 值大于预设阈值 p 时，我们可以认为该特定活动是一种常见活动 A_j。以下是所提出方法的逐步流程：

步骤1 ：使用多个居民用户的单一用途能耗数据（包括厨房、娱乐、家务等）计算 f(Q_{m,t})；

步骤2 ：使用EM算法识别对应于常见活动候选者的条件概率密度函数 f(Q_{m,t}|a_j)；

步骤3 ：对于个体消费者，评估观测到的用电量的 f(Q_{m,t}) 和 f(Q_{m,t}|a_j)，并求解方程 (2) 以得到先验概率 P(a_j)；

步骤4 ：使用公式 (3) 评估 P(a_j|Q_{m,t})；

步骤5 ：确定活动 a_j 的持续时间 G(a_j) 并计算 S(a_j)；

步骤6 ：确定阈值 p，以确定该消费者的日常活动 A_j。

III. 负荷曲线的重建

识别出的日常活动 A_j 根据其对应的概率 P(a_j) 分配到相应的时间段。使用 I(A_j, t) = P(a_j|Q_{m,t})，进而重构相应的电力消耗。该过程通过在每个时间段U中重新分配每个日常活动 a_j 来实现。每个日常活动的持续时间根据历史每日活动最早和最晚开始时间的随机性确定。特定时间段U中某项日常活动 a_j 的分配强度取决于其对应的概率 P(a_j|Q_{m,t})。当日常活动 A_j 被分配到24小时内每日消费者活动中后，再对每个日常活动 A_j 以及每个时间段U的历史用电数据，分析相应的条件概率密度函数 f(Q_{m,t}|A_j)，确定负荷曲线和用电量。由于用电量的确定具有概率特性，我们计算电力消耗置信区间而非单一估计，以便为配电公司规划人员提供更具可信性且不含偏差的预测。

相反，当活动 a_j 在时间段U的 P(a_j|Q_{m,t}) 值较高时，我们认为该活动 a_j 每天经常在该时间段进行，因此是一项常见活动。然而，这并不意味着我们预期同一活动会在每天相同的时间段内发生。因此，我们对一天内所有时间段的概率进行求和。由于活动持续时间较长，该预测值可能会增加，因此也相应增大。因此，我们对该值进行归一化处理，如下式所示：

$$
P_{norm}(a_j) = \frac{\sum_{t=1}^{24} P(a_j|Q_{m,t})}{\sum_{i=1}^{k} \sum_{t=1}^{24} P(a_i|Q_{m,t})}
$$

IV. 样本实例

本研究使用了2013年11月日本10户居民的历史消费数据进行分析。采用EM算法，图1显示了2013年11月每日厨房电器类别电力消耗的条件概率密度函数的混合分布。在厨房电器类别中共有10项活动a_j被识别出来。

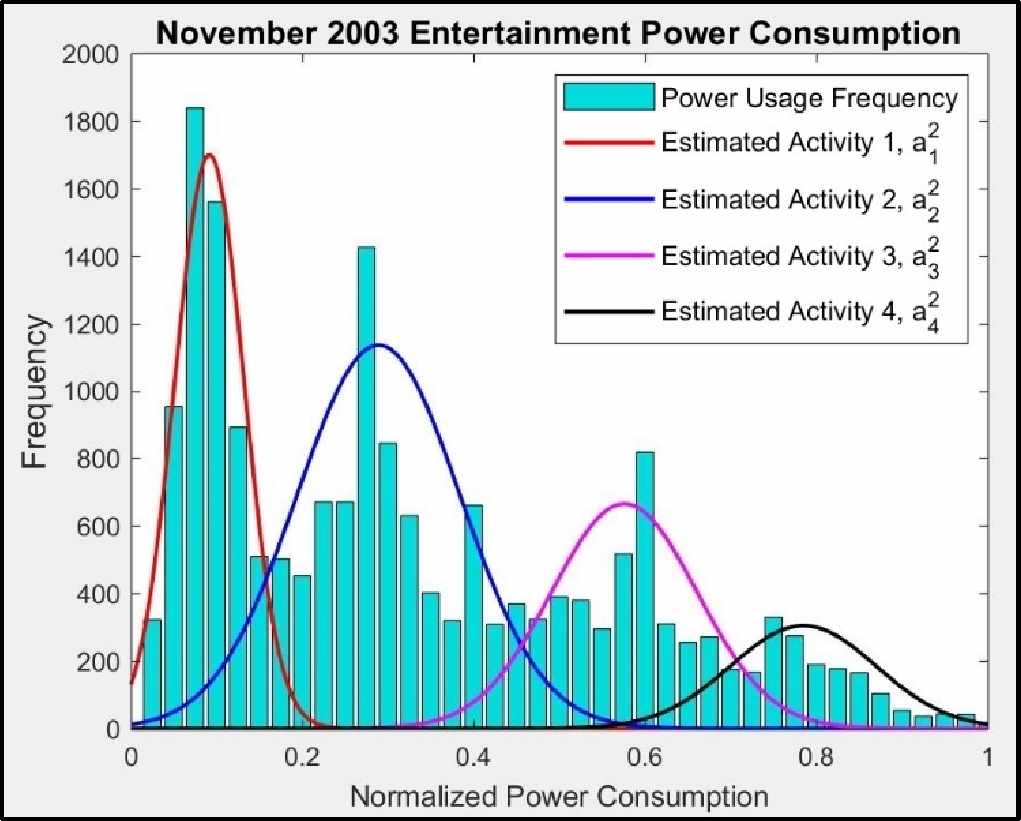
图2展示了在进行不同类型活动a_j的情况下，娱乐电器类别用电量的混合条件概率密度函数分布。

图3展示了在进行不同类型活动时，家用电器类别用电量的混合概率密度函数分布。

在使用EM算法确定 f(Q_{m,t}|a_j) 并用混合分布表示后，再使用最小二乘法（LSM）求解 P(a_j)，随后选取一个居民用户并计算公式(3)中的数值。

表1列出了预测结果。研究人员预设的阈值为p = 0.3，该值识别出该居民用户进行的7种常见活动A_j。其中，3项活动属于厨房用电类别，3项活动属于娱乐用电类别，1项活动属于家务用电类别。

活动a_j	G(A_j)
厨房 a_1	18
厨房 a_2	17
厨房 a_3	16
娱乐 a_4	19
娱乐 a_5	18
娱乐 a_6	17
家务 a_7	15

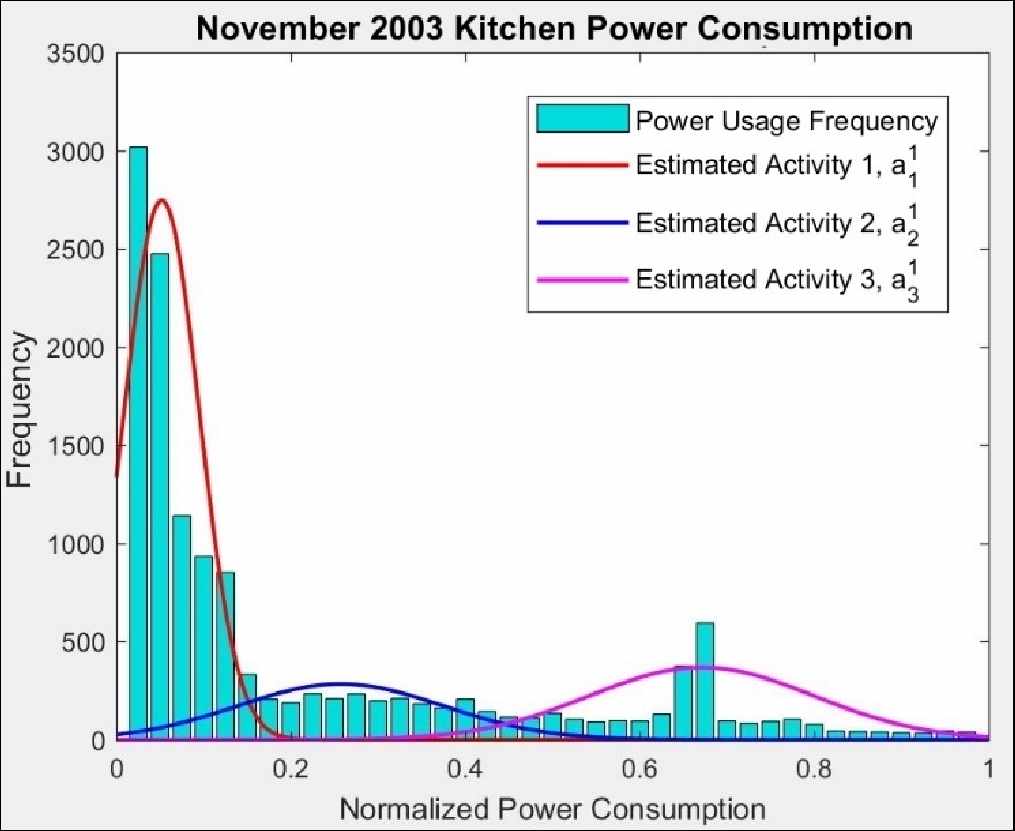
图4展示了在典型日特定居民用户的日负荷曲线和用电量重建的样本实例，其均方根误差（RMSE）为0.091125 kWh/h。

V. 结论

该实例取得了相对较好的效果，但由于所采用的方法本质上是概率性的，我们计算了用电量的置信区间而非单一估计，以便为配电公司规划人员提供更具可信性且不含偏差的预测。图5展示了任意连续8小时区间的置信度概率分析。根据图中结果，该特定居民用户的用电量约为0.4 kWh/h，其置信概率超过百分之九十五（95%）。

对每个时间段t重复进行置信度概率分析，以完成24小时日负荷曲线和用电量的估算。

图5展示了该特定消费者在2013年12月典型日的实际与重建负荷曲线和用电量。大约95%的实际日用电量落在重建的95%置信区间内。少数时间段的估计用电量区间与实际用电量存在较大差异，这可能是由于使用了2013年11月的用电数据来预测2013年12月的用电量，且该预测可能未充分考虑本研究未涵盖的气温等因素的影响。

本文提出了一种方法，该方法通过历史电力消耗数据识别居民消费者的日常活动，并重建其对应的每日负荷曲线，以为配电公司提供可靠的日常电力供应采购信息。研究结果表明，所提出的方法在识别居民消费者的日负荷曲线和用电量方面具有巨大潜力，特别是通过进一步纳入其他影响因素（如非日常活动、天气参数等）可进一步提升模型性能。