OpenAI开源0.4B参数Circuit-Sparsity模型：给AI大脑做次“极简手术”

原创 于 2025-12-18 21:00:26 发布 · 449 阅读 · 10 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#circuit #sparsity #OpenAI #0.4B参数模型 #开源模型 #人工智能

目录

前言

一、告别“身兼数职”的混乱

二、当“黑箱”变成“电路板”

三、代价昂贵的“透明”

四、未来的路：搭建“桥梁”

结语

🎬 攻城狮7号：个人主页

🔥 个人专栏:《AI前沿技术要闻》

⛺️ 君子慎独!

 🌈 大家好，欢迎来访我的博客！
⛳️ 此篇文章主要介绍 OpenAI开源0.4B参数Circuit-Sparsity模型
📚 本期文章收录在《AI前沿技术要闻》，大家有兴趣可以自行查看！
⛺️ 欢迎各位 ✔️ 点赞 👍 收藏 ⭐留言 📝！

前言

        不管是写代码、画图还是聊天，现在的AI大模型都已经强得离谱。但有一个问题始终悬在所有人心头：我们不知道它到底是怎么想的。

        我们喂给它数据，它吐出答案，中间的过程就像一个密封的黑箱。这种“不可解释性”，让医生不敢完全信任AI的诊断，让银行不敢把风控全权交给算法。

        最近，OpenAI干了一件反直觉的事。他们没有去造更大、更复杂的模型，而是发布了一个参数只有0.4亿（0.4B）、且99.9%的连接都被剪断的“残缺”模型——Circuit-Sparsity。

        这个看似“偷工减料”的模型，其实是OpenAI为了看懂AI大脑而进行的一次大胆手术。

一、告别“身兼数职”的混乱

        要理解OpenAI为什么要删掉99.9%的权重，我们先得看看传统的AI模型长什么样。

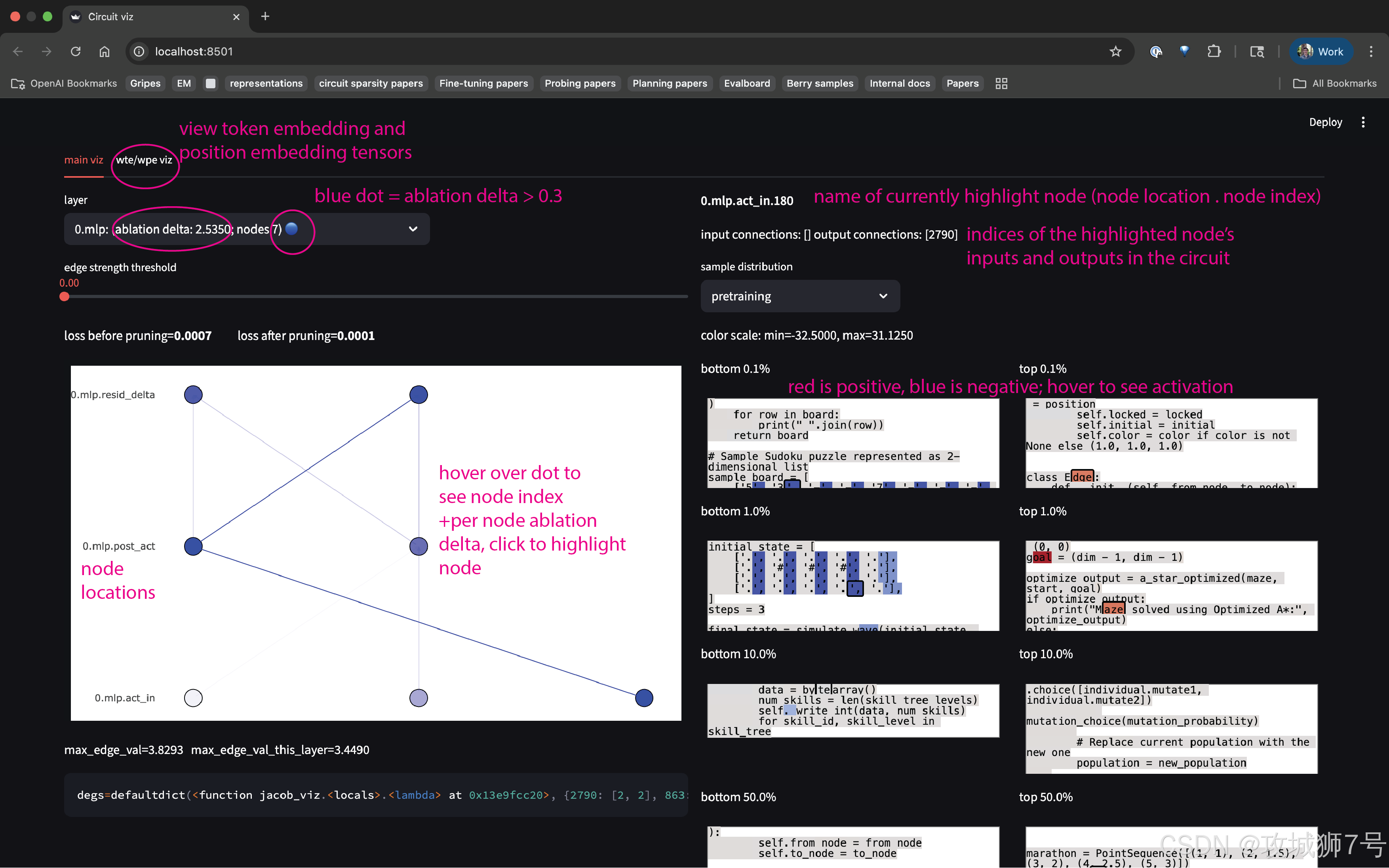
        目前的AI大模型（如GPT-4），其内部结构通常是“密集（Dense）”的。这就好比一个拥挤的办公室，里面的几千亿个神经元全都纠缠在一起。为了存下海量的知识，每个神经元都被迫通过“叠加态（Superposition）”来工作——也就是说，同一个神经元可能既要负责识别“猫的胡须”，又要负责理解“莎士比亚的十四行诗”，还要顺便处理一下“Python代码的缩进”。

        这种“身兼数职”的状态，导致当你试图去分析某个神经元时，根本搞不清它到底在干嘛。整个模型就像一团乱麻，牵一发而动全身，根本理不清楚逻辑流向。

        OpenAI的新思路是：强行拆散它们。

        通过“权重稀疏化（Weight Sparsity）”，OpenAI强制要求每个神经元只能和极少数的其他神经元“说话”。这就好比把那个拥挤的办公室拆了，给每个员工分配了独立的隔间，并且规定每个人只能干一件事。

        如果一个神经元只负责识别“猫”，那它就绝对不能去管“代码”。因为连接被切断了，它想管也管不了。

二、当“黑箱”变成“电路板”

        经过这种极致的“剪枝”后，奇迹发生了。

        OpenAI发现，在这个稀疏模型内部，自然涌现出了一种被称为“电路（Circuits）”的结构。这些电路不再是纠缠不清的乱网，而是像我们物理课上学的电路图一样，逻辑清晰、路径分明。

        举个栗子：引号闭合任务

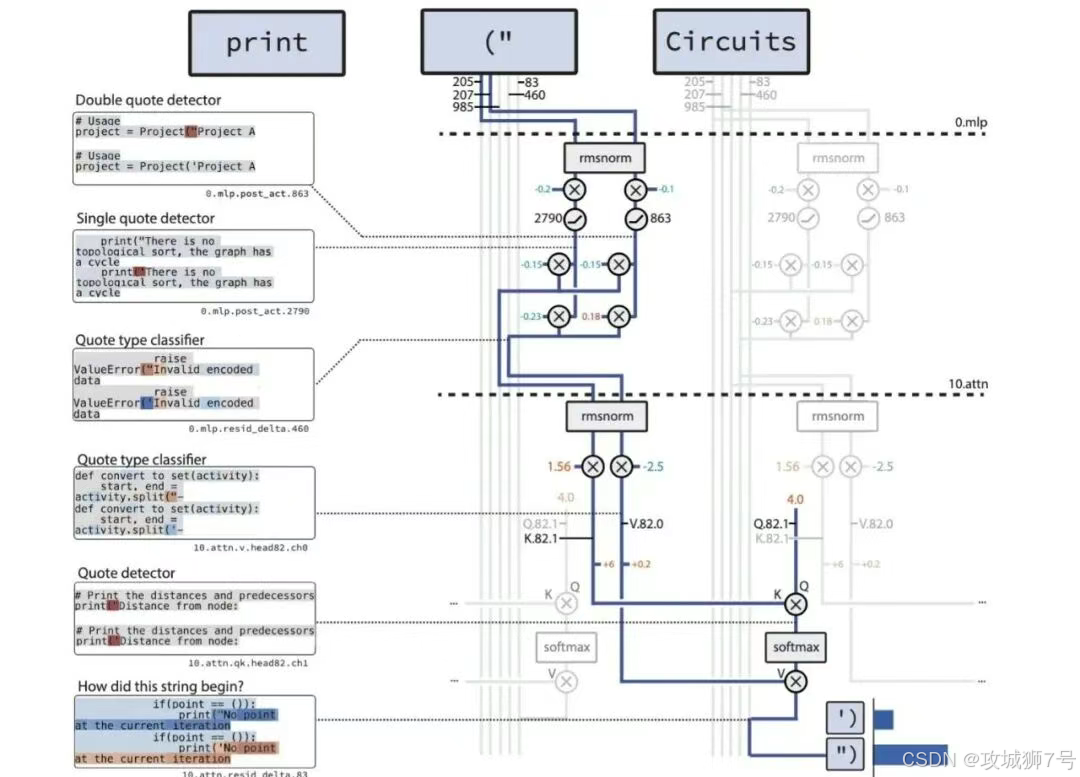
        为了验证这个模型是不是真的“变透明”了，研究人员给它布置了一个任务：检查一段Python代码里的字符串引号是否闭合（比如开头是单引号，结尾也得是单引号）。

        在以前的密集模型里，这个任务可能需要调动成百上千个神经元，混在各种无关的计算里，根本没法追踪。

        但在Circuit-Sparsity模型里，研究人员看到了一个令人感动的极简流程：

        （1）检测：有专门的神经元负责发现“哦，这里有个单引号”。

        （2）记录：另一个神经元像记账员一样，记下“现在的状态是单引号开启中”。

        （3）搬运：注意力机制把这个状态搬运到字符串结尾。

        （4）匹配：输出层根据状态，填上闭合的单引号。

        整个过程只用了十几个节点，就像一条精简的流水线。研究人员甚至做了个破坏性实验：把这条流水线上的关键节点切断，模型立马就不会做这题了；但如果切断其他几千个无关节点，模型毫发无损。

        这意味着，我们终于确切地找到了控制AI某项能力的“物理开关”。

三、代价昂贵的“透明”

        听到这里，你可能会问：既然稀疏模型这么好，逻辑清晰又可控，为什么大家不都用它？

        这就涉及到了理想与现实的差距。Circuit-Sparsity目前更像是一个实验室里的“概念车”，离量产上路还有很远的距离。

        核心痛点在于：慢，且贵。

        现在的GPU（图形处理器）是专门为密集矩阵运算设计的。对于GPU来说，算一个全是数字的矩阵，和算一个99%都是0的矩阵，花的时间其实差不多，甚至因为稀疏矩阵的数据结构不规则，读取起来反而更费劲。

        这就导致Circuit-Sparsity模型的运行效率极低，比同等规模的普通模型慢了100到1000倍。如果想把这一套用到GPT-4那种级别的千亿参数模型上，目前的算力成本是完全无法承受的。

        这就好比我们为了让电线走线整齐，不得不把原本的一根粗电缆拆成一万根细电线单独铺设，工程量和维护成本直接爆炸。

四、未来的路：搭建“桥梁”

        既然直接用稀疏模型太慢，那这个研究是不是就没用了？

        并不是。OpenAI提出了一种“曲线救国”的方案——桥梁网络（Bridges）。

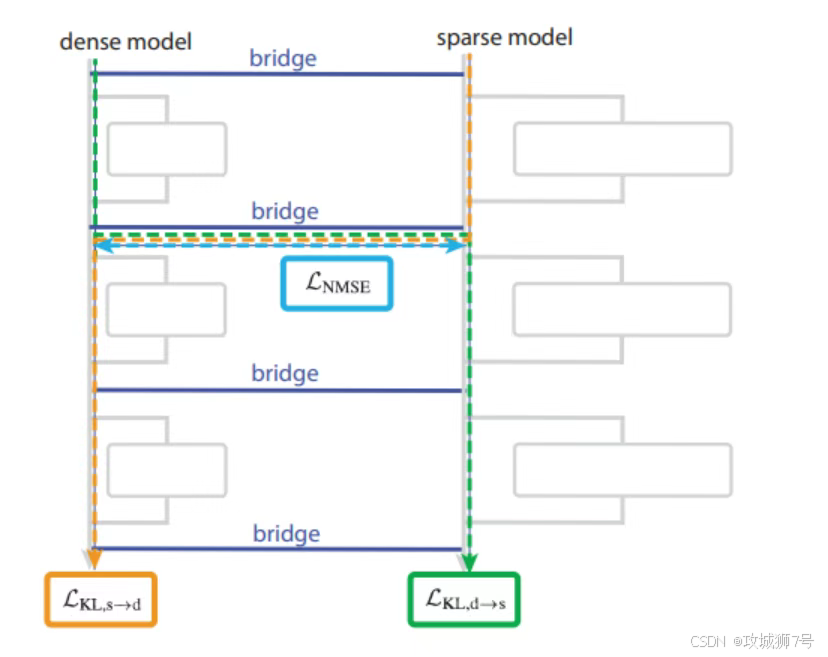
        既然我们看不懂强大的密集模型，那我们可以训练一个稀疏模型作为“替身”或“翻译官”。我们可以尝试建立一种映射关系，把密集模型里那些混乱的激活状态，翻译成稀疏模型里清晰的电路语言。

        或者，我们可以利用在稀疏模型里学到的原理，去反向“修剪”那些已经训练好的大模型，把那些不重要的乱七八糟的连接剪掉，只保留核心电路，从而在不重新训练的情况下提升可解释性。

结语

        OpenAI这次开源的Circuit-Sparsity，与其说是一个可以用的产品，不如说是一份在这个AI狂飙突进时代里的“冷静声明”。

        它告诉我们，人工智能不应该永远是一个充满玄学的黑箱。通过精心的设计和约束，我们完全有能力让机器的思维过程变得像钟表一样精确可见。

        虽然距离让GPT-5变得完全透明还有很长的路要走，但至少，我们现在知道第一步该迈向哪里了。从“知其然”到“知其所以然”，这或许才是AI通向真正安全的必经之路。

开源地址：https://github.com/openai/circuit_sparsity
模型下载：https://huggingface.co/openai/circuit-sparsity

看到这里了还不给博主点一个：
⛳️ 点赞☀️收藏 ⭐️ 关注！
💛 💙 💜 ❤️ 💚💓 💗 💕 💞 💘 💖
再次感谢大家的支持！
你们的点赞就是博主更新最大的动力！

最强开源模型 Mixtral-8x7B-Instruct-v0.1 详细介绍：稀疏 Mixtral of experts
AI天才研究院
02-02 1660
同样，在推理过程中，假设每个令牌仅使用两名专家，推理速度 (FLOP) 就像使用 12B 模型（而不是 14B 模型），因为它计算 2x7B 矩阵乘法，但共享一些层。然后，输入的信息将以最高的概率发送给专家，确保最合适的专家处理手头的任务。C) 另请注意，虽然有推理服务，但实现了 FP8 实现，每个令牌运行 3 个专家（而不是默认的 2 个）——但激活更多专家是有害的，因为该模型经过训练只需要处理 3 个专家的贡献2个顶级的。它是最强大的开放权重模型，具有宽松的许可证，也是成本/性能权衡方面的最佳模型。
OpenAI开源“Circuit‑Sparsity”模型，0.4 B 参数实现 99.9% 权重归零！
Aiadsgo的博客
12-15 307
Circuit‑Sparsity 的发布标志着大模型从“黑箱”向“可解释”迈出了重要一步。虽然当前仍面临计算效率的挑战，但其在模型结构简化、决策路径可视化方面的突破，为 AI 在高风险行业的安全落地提供了新的技术路径。随着桥梁网络等后续方案的完善，稀疏模型有望在保持可解释性的同时，逐步缩小与主流密集模型的性能差距，推动人工智能向更透明、更可靠的方向发展。
OpenAI又开源了！仅0.4B，给模型大瘦身
最新发布
Everly_的博客
12-18 348
OpenAI研究团队的这项研究，标志着AI可解释性领域的一项重要突破，也印证了理解AI并非遥不可及的目标。研究团队在论文博客中称，这项工作是迈向更宏大目标的早期探索。接下来，他们计划将相关技术扩展至更大规模的模型，同时进一步解释更多模型的行为逻辑。为解决稀疏模型训练效率低下的问题，团队提出了两个后续研究方向：一是从现有密集模型中提取稀疏电路，替代“从头训练稀疏模型”的传统方式；二是研发更高效的可解释性模型训练技术，推动相关技术更易落地生产。
OpenAI 突然开源了一个“只有 0.4B 参数”的模型——
gaetoneai的博客
12-16 323
高风险决策？用 Circuit Sparsity，路径可审计；实时边缘推理？用它，省电又快；教学/研究？它是绝佳的“白盒 AI”范例。但前提是——你得能轻松用上它，而不是被集成复杂度劝退。
OpenAI新动作：仅0.4B参数，模型大瘦身时代来临！
Android23333的博客
12-18 421
OpenAI开源Circuit-Sparsity模型，通过99.9%权重清零技术使大模型内部形成可读"电路"，解决了AI决策不可解释的问题。这一技术使神经元激活具有明确语义，电路规模缩小16倍，但计算效率较低，速度慢100-1000倍。研究团队提出"桥梁网络"方案，试图连接稀疏模型与密集模型，为AI可解释性提供新思路。
OpenAI开源新模型揭秘大语言模型的可解释性！
2401_84204207的博客
12-15 689
OpenAI今日放出一个新模型 circuit-sparsity，大小只有0.4B参数，类似GPT-2架构的语言模型，主要用于理解模型，即模型的可解释性。
OpenAI开源了一个“瘦身版“AI：让神经网络从黑箱变透明
LXZZKJ的博客
12-15 1125
OpenAI开源了仅0.4B参数的稀疏模型，99.9%参数为零，颠覆了当前大模型的发展趋势。该技术通过动态Top-K剪枝、AbsTopK激活稀疏化和架构微调三大支柱，实现了模型的高度可解释性。研究表明，稀疏模型能形成清晰的任务电路，如Python引号匹配仅需122个节点，比密集模型小16倍。虽然训练成本是密集模型的100-1000倍，且不适合创意写作等复杂任务，但这项技术为AI可解释性开辟了新路径。未来可能采用分层架构、专用硬件或"桥梁"技术来降低应用门槛。这一突破标志着AI发展从单纯追
OpenAI突然开源新模型！99.9%的权重是0，新稀疏性方法代替MoE
阿木寺的博客
12-14 10
这是一种通过人为约束模型内部连接的稀疏性，让模型计算过程可拆解、可理解的大语言模型变体，本质上是为了解决传统稠密Transformer的黑箱问题，让内部的计算电路能被人类清晰解读，知道AI是如何做决策的，避免轻易相信AI的胡话（doge）。咱们平时用的传统大模型，内部神经元连接得密密麻麻，权重矩阵几乎全为非零值，信息传递呈现出高度叠加状态，就像一团扯不开的乱线，没人能说清它是怎么得出某个结论的。并且，这项工作也只是AI可解释性探索的早期一步，未来团队计划将技术扩展到更大的模型，解锁更复杂的推理电路。
告别“烧钱”训练！OpenAI开源“减肥版”大模型，效果不变，成本暴跌99%！
m0_59163425的博客
12-16 858
【AI行业动态摘要】 OpenAI开源0.4B稀疏模型Circuit-Sparsity，通过99.9%权重稀疏化提升模型可解释性，但计算效率下降显著；谷歌搜索广告业务未受AI冲击，Meta战略转向AI可穿戴设备，缩减元宇宙投入。谷歌DeepMind研究揭示多智能体系统存在"规模悖论"，AI在抗衰老研究中取得突破，Anthropic提出哲学化提示词工程优化人机交互。创投方面，宇树科技斥资1亿竞标春晚赞助，荷兰Nebius获微软194亿美元算力大单，反映AI基础设施需求激增。当前AI发展呈现
使用稀疏自编码器（Sparse Autoencoders, SAEs）提升语言模型的可解释性
阿正的梦工坊
04-23 1954
Cunningham 等人在论文《Sparse Autoencoders Find Highly Interpretable Features in Language Models》中提出了一种基于稀疏自编码器（Sparse Autoencoders, SAEs）的无监督方法，旨在解决语言模型中特征的多义性（Polysemanticity）和叠加（Superposition）问题，从而提取更具可解释性和单义性（Monosemantic）的特征。
matlab终止以下代码-structural-sparsity:具有潜在变量的稀疏图的结构学习
05-21
结构稀疏模型学习稀疏图来组织对象集。 该算法搜索说明特征的图，同时支持稀疏图结构。 每个图定义具有潜在变量的高斯马尔可夫随机场。 请引用以下论文： 预印本可在arXiv：1611.09384上获得。 要求 在运行代码之前...
精选资源
vggnet代码matlab-Structure-Sparsity:banyungong
05-27
具有结构化稀疏性的稀疏深度神经网络 这是针对结构化的稀疏深层神经网络的独立源代码，可加快对深层神经网络（DNN）的评估。 技术细节在下面的文章中：学习深度神经网络中的结构稀疏性。 我们的SSL（结构稀疏学习）...
精选资源
matlab贝叶斯阈值代码-Bayesian-Hierarchical-Varying-sparsity-Regression-Models-
05-28
matlab贝叶斯阈值代码贝叶斯层次可变稀疏回归模型及其在癌症蛋白质组学中的应用 作者贡献清单表 数据 抽象的 该数据集包含四种癌症（肾脏肾透明细胞癌，卵巢浆液性囊腺癌，皮肤皮肤黑色素瘤和头颈部鳞状细胞癌）的...
大模型学习基础（五） 强化学习（Reinforcement Learning，RL）初步
qq_56095294的博客
12-13 338
前面的文章简单介绍过，传统的监督学习所使用的数据集是（特征，标签），有“标签”即明确的知晓正确的输出应该是什么。而实际的情况是，环境的状态S是由多个Si构成的，每训练一组S-a即训练一个多分类问题，把这些问题的损失函数（交叉熵）加在一起，即可训练出在不同的状态下应该使用什么动作。模型在选择一个动作之后，这个动作实际是对Environment发生，相应的Environment会给模型一个回馈Reward，然后再给模型一个新的Observation，模型继续选择新的动作，循环此过程。
数据分析Agent白皮书：揭秘Data x AI的底层逻辑与未来关键
LyAGent的博客
12-18 336
《2025数据分析Agent白皮书》指出，数据分析Agent正成为AI落地的核心形态，实现从"人人分析"到"人人消费"的转变。白皮书系统解析了其技术架构（包括Query/Document/DeepAnalyze三大Agent能力）、行业实践（能源/制造/零售等领域）及落地路径，强调需突破数据准度、分析深度与消费广度三大挑战。未来，数据分析Agent将深度融入业务流程，推动"洞察即行动"的自动化决策模式。该技术有望彻底改变企业数据消费方式，使数据智能
以太联的自愈功能与看门狗机制解析
suzhou_speeder的博客
12-15 1093
看门狗(Watchdog)是一种硬件或软件实现的定时器机制，其核心功能是监控系统或程序的运行状态，防止程序跑飞或陷入死循环。案例：车载以太网交换机通过硬件看门狗实时监测链路状态，若检测到链路中断(如3ms内未收到心跳包)，立即启用备用路径，确保刹车、转向等关键系统永不掉线。案例：某智能工厂的PLC(可编程逻辑控制器)采用软件看门狗，若主程序因干扰死机，看门狗机制自动重启PLC，恢复生产流程。三者协同工作，实现“设备-交换机-网络”三级自愈，显著提升网络可靠性、降低运维成本，并为企业数字化转型提供坚实基础。
多模态赋能情绪理解：Qwen3-VL+LLaMA-Factory 的人脸情绪识别实战
Lab4AI的博客
12-17 499
本项目依托Lab4AI平台，基于LLaMA-Factory成功对Qwen3-VL进行了完整的微调流程。我们将传统的人脸情绪识别任务与多模态大语言模型（MLLM）相结合，探索了MLLM在视觉情绪理解中的应用。通过微调Qwen3-VL，我们成功将传统的分类任务转化为多模态推理任务，显著提升了模型在复杂场景下的鲁棒性和准确率。这一方案不仅在人脸情绪识别上取得了显著提升，还为其他视觉任务的多模态大模型应用提供了新的思路，具有广泛的应用前景。
Transformer架构的原理是什么？
SACKings的博客
12-15 712
对于“Thinking”这个词，它的输出向量可能包含了90%它自己的信息和10%“Machines”的信息。而对于“Machines”，它的输出可能包含了70%它自己的信息和30%“Thinking”的信息。Transformer 架构的原理是理解现代大模型（如 GPT、BERT、T5 等）的基石。正是因为这些原理上的优势，Transformer才取代了RNN和CNN，成为了当今AI大模型时代的统治性架构。的（打乱输入顺序，输出可能不变），它没有内置的位置概念。Q·K 然后Softmax。
AIDD-人工智能药物设计-扩散模型热力学：从 AI 提取物理能量
itwangyang520的博客
12-14 1112
扩散模型的核心是加噪与去噪。这对业界的启示是，要实现精准医疗，特别是针对耐药突变的药物设计，不能仅依赖大语言模型（Large Language Model, LLM）处理序列。他们从文献和数据库中挖掘了过去被忽略的细节：氨基酸的替换、插入、缺失，以及关键的磷酸化修饰，最终整理出 4032 对新的激酶 - 配体数据。GeneGPT 曾展示了大语言模型（LLM）在生物医药领域的潜力，而 OpenBioLLM 提出了不同于 GeneGPT 单体（Monolithic）架构的方案：组建由「专家」构成的团队。
🔄 Dictionary Learning Iteration 1/30 🔍 Sparsity Check: → X non-zero ratio: 0.0390 → Mean abs value of X: 0.393725 → Max |x_i|: 1.259230 → Num atoms used per signal: 11346.00 → Normalized Recon Error: 0.990054, Dict Update Norm: 186.153414 🔄 Dictionary Learning Iteration 2/30 🔍 Sparsity Check: → X non-zero ratio: 0.0390 → Mean abs value of X: 21.304038 → Max |x_i|: 634.062207 → Num atoms used per signal: 11346.00 → Normalized Recon Error: 0.987390, Dict Update Norm: 182.732271 🔄 Dictionary Learning Iteration 3/30 🔍 Sparsity Check: → X non-zero ratio: 0.0390 → Mean abs value of X: 11587.156838 → Max |x_i|: 321501.663110 → Num atoms used per signal: 11346.00
12-06
你提供的调试信息暴露了一个**极其严重的问题**： ```text Iter 1: → X non-zero ratio: 0.0390 ✅ 正常稀疏性 → Mean abs value of X: 0.393725 ✅ 合理数值范围 → Max |x_i|: 1.259 ✅ 小幅系数 Iter 2: → Mean abs value of X: 21.3 ⚠️ 开始变大！ → Max |x_i|: 634 ❗ 溢出警告！ Iter 3: → Mean abs value of X: 11,587 ❌ 爆炸！ → Max |x_i|: 321,501 💥 数值溢出 → Num atoms used per signal: 11346 ❌ 每个信号用了 11346 个原子？！ ``` --- ## 🚨 核心问题诊断 ### 🔴 问题 1：`Num atoms used per signal = 11346` → **不可能！** - 假设你有 `N=500` 个信号，`sparsity_level=L` - 那么每个信号最多只能用 `L` 个原子（比如 3~10） - **但这里显示每个信号用了 11346 个原子？！** 👉 表明：你的 `Omega[i]` 存储的是**所有非零元素的全局索引**，而不是单个信号的支撑集！ --- ## ✅ 错误根源：`sparse_coding_with_support` 中的 `Omega` 构建方式错误 你可能写了类似这样的代码： ```python Omega = np.where(X != 0)[0] # ❌ 返回的是 (K*N,) 的全局索引 ``` 或者： ```python Omega = [list(np.nonzero(X[:, i])[0]) for i in range(N)] # 但如果 X 在之前被错误更新过，会导致每列有上千个非零项 ``` 但更关键的是： > 🔥 **X 的系数爆炸增长 → 说明字典和系数之间发生了正反馈循环** --- ## 🔥 问题 2：`X` 的系数爆炸 → 字典学习发散 从： - Iter1: max |x_i| = 1.26 - Iter2: max |x_i| = 634 - Iter3: max |x_i| = 321,501 这是一个典型的 **几何级数增长**（约 ×500/次），说明： > ❌ **你在某处把 `X` 更新成了最小二乘解而没有稀疏性约束！** > > 或者： > > ❌ **在残差上做了无约束拟合，导致 TLS 更新放大了误差** --- ## ✅ 必须立即修复的 3 个地方 --- ### ✅ 修复 1：确保 `sparsity_level` 是每个信号的最大原子数 ```python sparsity_level = 3 # 每个信号最多使用 3 个原子 ``` 并在 OMP 中严格限制迭代次数： ```python for _ in range(max_atoms): # max_atoms = sparsity_level ... ``` --- ### ✅ 修复 2：重写 `orthogonal_matching_pursuit` 函数（保证正确性） ```python def orthogonal_matching_pursuit(Y, D, max_atoms): """ 对每个信号 y_i 使用 OMP 求解稀疏表示 x_i 参数: Y: (d, N) 信号矩阵 D: (d, K) 字典 max_atoms: L, 最大非零数（稀疏度） 返回: X: (K, N), 稀疏系数矩阵 Omega: list of lists, 每个信号的支撑集 """ d, N = Y.shape K = D.shape[1] X = np.zeros((K, N)) Omega = [[] for _ in range(N)] for i in range(N): y = Y[:, i].copy() residual = y.copy() omega_i = [] # 当前信号的支撑集 for _ in range(max_atoms): # 计算相关性 correlations = np.abs(D.T @ residual) best_atom = np.argmax(correlations) if best_atom in omega_i: continue # 防止重复选 omega_i.append(best_atom) # 构造子字典并求最小二乘解 D_sub = D[:, omega_i] try: x_sub, _, _, _ = np.linalg.lstsq(D_sub, y, rcond=1e-6) except: break # 更新残差 x_full = np.zeros(K) x_full[omega_i] = x_sub residual = y - D @ x_full # 提前收敛 if np.linalg.norm(residual) < 1e-6: break # 存储结果 X[omega_i, i] = x_sub Omega[i] = omega_i return X, Omega ``` --- ### ✅ 修复 3：禁止在主循环中对 `X` 做额外 LS 优化（除非可控） 你现在可能在主循环里加了这段： ```python # ❌ 危险！如果没有限制支撑集，会引入新非零项 for i in range(N): omega_i = np.where(X[:, i] != 0)[0] if len(omega_i) == 0: continue D_omega = D[:, omega_i] x_opt, *_ = np.linalg.lstsq(D_omega, Y[:, i], rcond=1e-6) X[omega_i, i] = x_opt # ✅ 只改已有位置，不新增 → 安全 ``` ✅ 这段其实可以保留，因为它只在原有支撑集上优化，不会增加稀疏度。 但必须确认：`omega_i` 真的是该列的非零索引。 --- ### ✅ 修复 4：检查 `blotless_update` 是否修改了 `X` 确保你没有在这段代码中做任何关于 `X` 的赋值： ```python def blotless_update(D, X, Y, num_atoms, block_size=4): ... for block_idx in range(num_blocks): T = slice(start, end) D_T = D[:, T].copy() X_rest = X.copy() X_rest[T, :] = 0 Y_residual = Y - D @ X_rest D_T_new = solve_tls_correct(Y_residual, D_T) D[:, T] = D_T_new # ✅ 只更新 D # ❌ 绝对禁止： # X[T, :] = new_X_T # 或运行 sparse_coding_with_support(...) ... return D, X, dict_update_norm ``` --- ### ✅ 修复 5：归一化策略要一致 每次更新完 `D` 后，必须重新单位化，并将尺度转移到 `X`： ```python norms = np.linalg.norm(D, axis=0, keepdims=True) + 1e-8 D /= norms X *= norms.T # 把尺度还给 X ``` 否则某些原子会越来越大，导致 `X` 越来越小或反之，引发不稳定。 --- ## ✅ 添加防御性检查（强烈建议） 在每轮迭代末尾加入： ```python # 检查 X 是否失控 if np.max(np.abs(X)) > 1e3: print("🚨 X 系数爆炸！最大值 =", np.max(np.abs(X))) print("🛑 中止训练") break # 检查每列稀疏度 nnz_per_col = np.array([len(Omega[i]) for i in range(len(Omega))]) if np.mean(nnz_per_col) > 2 * sparsity_level: print(f"⚠️ 平均使用原子数 {np.mean(nnz_per_col):.2f} > 2×目标稀疏度 {sparsity_level}") ``` --- ## ✅ 预期修复后输出 ```text Iter 1: → X non-zero ratio: 0.0300 → Mean abs value of X: 0.45 → Max |x_i|: 1.8 → Atoms/signal: 3.0 → Recon Error: 0.81 Iter 2: → Mean abs value: 0.51 → Max |x_i|: 2.1 → Recon Error: 0.72 ↓ ... Iter 10: → Recon Error: 0.51 ↓ ``` 即：**X 的幅度稳定在合理范围，误差持续下降** --- ###
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

攻城狮7号

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值