JZOJ4819. 【NOIP2016提高A组模拟10.15】算循环

Description

Input

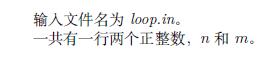
Output

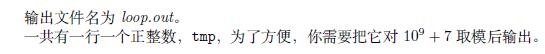
Sample Input

167 198

Sample Output

906462341

Data Constraint

分析

题目的意思就要求：
$Ans=\sum_{i=1}^n \sum_{j=1}^m \sum_{k=i}^n \sum_{l=j}^m \sum_{x=i}^k \sum_{y=j}^l 1$
我们就对这条式子进行化简

首先，先去掉x和y的循环
$Ans=\sum_{i=1}^n \sum_{j=1}^m \sum_{k=i}^n \sum_{l=j}^m (l-j+1)*(k-i+1)$

下一步，将l的循环去掉。
不妨设a=(k-i+1)
则$Ans=\sum_{i=1}^n \sum_{j=1}^m \sum_{k=i}^n \sum_{l=j}^m a*(l-j+1)$
$Ans=\sum_{i=1}^n \sum_{j=1}^m \sum_{k=i}^n a+2a+3a+...+(m-j+1)*a$
$Ans=\sum_{i=1}^n \sum_{j=1}^m \sum_{k=i}^n (m-j+1)*(m-j+2)*(k-i+1)÷2$
同理，将k的循环去掉
$Ans=\sum_{i=1}^n \sum_{j=1}^m (m-j+1)*(m-j+2)*(n-i+1)*(n-i+2)÷4$

再接下来，我们尝试将j的循环去掉。
设b=(n-i+1)*(n-i+2)÷4
$Ans=\sum_{i=1}^n 1*2*b+2*3*b+3*4*b+...+m*(m+1)*b$
$Ans=\sum_{i=1}^n b*(1^1+1+2^2+2+3^3+3+...+m^2+m)$
$Ans=\sum_{i=1}^n b*m*(m+1)*(2*m+4)÷6$
$Ans=\sum_{i=1}^n (n-i+1)*(n-i+2)*m*(m+1)*(2*m+4)÷24$

最后将i的循环去掉，得到一个O(1)的公式：
$Ans=m*n*(m+1)*(n+1)*(2*m+4)*(2*n+4)÷144$

一个小优化：逆元可以预处理。

code(c++)

#include <cstdio> 
#define ll long long 
#define _ %1000000007 
using namespace std;
ll get(ll x){return (x*(x+1)_)*((x*2+4)_)_;}
int main()
{
    //freopen("loop.in","r",stdin);
    //freopen("loop.out","w",stdout);
    ll n,m;
    scanf("%lld%lld",&n,&m);
    ll t=506944448;
    printf("%lld\n",((get(n _)*get(m _))_)*t _);
}