leetcode 673. Number of Longest Increasing Subsequence（最长递增子序列数量DP + BinarySearch）

Given an integer array nums, return the number of longest increasing subsequences.

Notice that the sequence has to be strictly increasing.

Example 1:

Input: nums = [1,3,5,4,7]
Output: 2
Explanation: The two longest increasing subsequences are [1, 3, 4, 7] and [1, 3, 5, 7].
Example 2:

Input: nums = [2,2,2,2,2]
Output: 5
Explanation: The length of longest continuous increasing subsequence is 1, and there are 5 subsequences’ length is 1, so output 5.

给出一个数组，找出其中一共有几个最长子序列

思路：
(1) DP
有两步，一个是找最长递增子序列，一个是最长递增子序列的个数。
那么一个DP数组len保存递增子序列的长度，一个DP数组count保存递增子序列个数。

因为数组不是升序排列的，所以到 i 时，要去和0～i-1所有的元素比较，找到nums[i] > nums[j] ，那么到i 的递增子序列的长度len[ i ]是在len[j] 长度的基础上+1，选择所有len[j]中最大的一个，得到len[i]

同样的，count遍历到i 时，也需要再遍历0～i-1的所有元素， 第一次找到nums[i] > nums[j] 时，可以直接把nums[i]接在nums[ j ]后面，因为它们是同一个子序列，所以count[i] = count[j]。

如果在0~i-1的元素中又发现了新的nums[i] > nums[ j1 ]，那么nums[i]也可以接在nums[ j1 ]后面形成新的子序列。这时count[i] = count[j] + count[ j1 ]。
那么如何判断是第一次发现了nums[ j ]，还是后面又发现了新的nums[ j1 ]?可以借助长度来判断，如果len[i] == len[j] + 1, 就说明nums[i ] 已经接在在nums[j ]的后面了，如果len[i] < len[j] + 1,，就说明是第一次发现的，还没接成递增子序列。

每次遍历，更新最大子序列的长度。
最后再把数组遍历一次，把序列长度==最大序列长度的count加起来，就是结果。
时间复杂度O(n²)

//33ms
    public int findNumberOfLIS(int[] nums) {
        if(nums == null || nums.length == 0) {
            return 0;
        }
        
        int n = nums.length;
        int[] len = new int[n];
        int[] count = new int[n];
        int result = 0;
        int maxLen = 1;
                
        for(int i = 0; i < n; i++) {
            len[i] = 1;
            count[i] = 1;
            for(int j = 0; j < i; j++) {
                if(nums[i] > nums[j]) {
                    if(len[i] == len[j] + 1) {
                        count[i] += count[j];
                    } else if(len[j] + 1 > len[i]) {
                        len[i] = len[j] + 1;
                        count[i] = count[j];
                    }
                    
                    maxLen = Math.max(maxLen, len[i]);
                }
                
            }
        }
        
        for(int i = 0; i < n; i ++) {
            if(len[i] == maxLen) {
                result += count[i];
            }
        }
        
        return result;
    }

(2) BinarySearch
个人认为还是DP思路简单些，虽然说这个方法时间复杂度O(nlogn)
可以想象一下扑克牌游戏的空当接龙，每一竖排的扑克都是从大到小排列的。但是有如下规则：

1. 当新来一个数字不能再排到第一排的下面时（比最下面的数字大，又不能插到中间），就新开辟一排，把这个新来的数字当首数字。
2. 当新来一个数字同时满足可以放到第一排和第二排下面时，优先最左边，也就是第一排。

可以参考如下图，参考资料

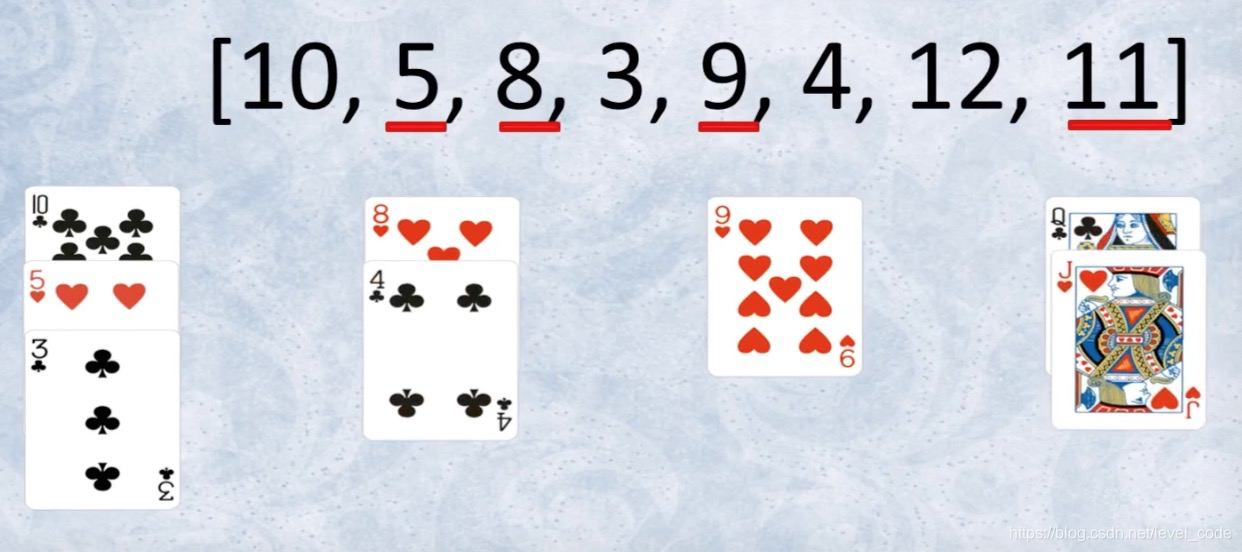
所以新来一个数字，首先要在所有竖排中搜索它应该放在第几竖排，这时是和每竖排的最小数字比较（因为规则1，不能在中间插入）。如果最小数字比新来的数字小，就新加一竖排。
如果锁定了某一竖排，就把数字挂在下面，一个竖排的count从上到下累加，这就方便我们可以取任意一段的count和。
如果新开辟一竖排，那么新开辟那个数字的count，就等于它前面一竖排的最小数字到比它大的数字这段的count和（用累加数组相减即可），搜索这个比它大的数字又用到一次Binary search。
举个例子，[1,3,8,5,4,7,6]
1开辟第一竖排, 保存（num, count)

(1, 1)

然后来了3， 比1大，所以又开辟一排，8又开辟一排

(1,1)  (3,1)  (8,1)

然后来了5，比8小，可以挂在8的下面，又来了4，比5小，挂在5的下面，5的累加count=2, 4的累加count是3

(1,1)  (3,1)  (8,1)
              (5,2)
              (4,3)

然后来了7，比所有排的末尾数字都大，不能挂在任何一个下面，所以新开辟一排。那么7的count怎么算呢，算它前面一排，也就是8开头的，这一排最下面的count，减去比7大的数字，也就是8的count，即3-1=2
这个逻辑很简单，可以和7形成递增子序列的，前面应该都是比7小的数，前面的递增子序列一共有3个，其中1，3，8这个序列是不满足后面加上7的，所以找到比7大的第一个数字，它前面的都不满足，就直接减去这个数字的count即可。

(1,1)  (3,1)  (8,1)  (7,2)
              (5,2)
              (4,3)

最后是6，要挂在7下面，同样要搜索它前面一排最后一个数的count，再减去比它大的8的count，同样得到了count=2。因为它挂在7下面，再求这一竖排count的累加和。最终6的count=4.
因为我们计算的时候一竖排的count是累加的，返回的时候只需要返回最后一排的末尾数字的count即可。

(1,1)  (3,1)  (8,1)  (7,2)
              (5,2)  (6,4)
              (4,3)

    public int findNumberOfLIS(int[] nums) {
        if(nums == null || nums.length == 0) {
            return 0;
        }
        
        int n = nums.length;
        if(n == 1) {
            return 1;
        }
        List<int[]>[] lists = (List<int[]>[])new ArrayList[n+1]; //List数组
        lists[1] = new ArrayList<int[]>();
        lists[1].add(new int[]{nums[0], 1});
        
        
        int len = 1;  //递增子序列长度,也是竖排的个数
        for(int i = 1; i < n; i++) {
            //搜索竖排
            int L = 1;
            int R = len + 1;
            while(L < R) {
                int M = L + (R-L) / 2;
                List<int[]> cur = lists[M];
                if(cur.get(cur.size()-1)[0] >= nums[i]) {
                    R = M;
                } else {
                    L = M + 1;
                }
            }
            
            if(L - 1 == len) { //要开辟新的一排
                lists[++len] = new ArrayList<int[]>();
            }
            
            int count = 0;
            if(L > 1) { //如果在第一竖排，不需要在前一排搜索了
                List<int[]> pre = lists[L-1];
                //在前一竖排中搜索比新数字大的
                int left = pre.size()-1; //最下面的数字小，上面数字大
                int right = -1;
            
                while(left > right) {
                    int mid = left + (right - left) / 2;
                    if(pre.get(mid)[0] < nums[i]) {
                        left = mid - 1;
                    } else {
                        right = mid;
                    }
                }
                count = pre.get(pre.size()-1)[1] - (left >= 0 ? pre.get(left)[1] : 0);
            } else {
                count = 1;
            }
            
            //当前竖排的count累加
            count += (lists[L].size() == 0) ? 0 : lists[L].get(lists[L].size()-1)[1];
            lists[L].add(new int[]{nums[i], count});
                        
        }
        //最后一排的最后数字的count，注意最后一排不是lists[n]
        return lists[len].get(lists[len].size()-1)[1];
    }