leetcode 688. Knight Probability in Chessboard（棋盘中马的概率）

On an NxN chessboard, a knight starts at the r-th row and c-th column and attempts to make exactly K moves. The rows and columns are 0 indexed, so the top-left square is (0, 0), and the bottom-right square is (N-1, N-1).

A chess knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.

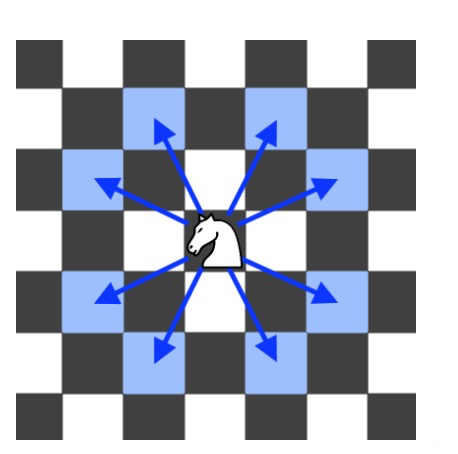
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.

The knight continues moving until it has made exactly K moves or has moved off the chessboard. Return the probability that the knight remains on the board after it has stopped moving.

Example:

Input: 3, 2, 0, 0
Output: 0.0625
Explanation: There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.

给出一个NxN的棋盘，在(r, c)的位置放上“马”，象棋中“马走日，象走田”。马可以走K步，问K步走完时“马”还留在棋盘上没有出界的概率。

思路：
DFS
马走完一步后，重复递归。
但是直接DFS会有很多重复的计算，因此把每一步的计算都保存起来。
在(r, c)位置且还剩k步的时候留在棋盘上的概率是一定的。定义三维DP数组。保存dp[r][c][k]

至于马可走的8个方向，可直接一步到位定义8个r，c的移动，也可以先走水平或垂直的2步，再走正交方向的一步。

直接一步到位的8个方向

//5ms
class Solution {
    Double[][][] dp;
    public double knightProbability(int N, int K, int r, int c) {   
        dp = new Double[N][N][K+1];
        return dfs(N, r, c, K);
    }
    
    double dfs(int N, int cr, int cc, int k) {
        if(cr < 0 || cr >= N || cc < 0 || cc >= N) {
            return 0;
        }
        
        if(k <= 0) {
            return 1.0;
        }
        
        if(dp[cr][cc][k] != null) {
            return (double)dp[cr][cc][k];
        }
        
        double prob = 0;
        int[][] dirc = new int[][]{{-2,-1},{-2,1},{-1,-2},{-1,2}, 
                                 {1,-2}, {1,2}, {2,-1}, {2,1}};
        for(int i = 0; i < 8; i++) {
            int row = cr + dirc[i][0];
            int col = cc + dirc[i][1];
            if(row < 0 || row >= N || col < 0 || col >= N) continue;
            prob += dfs(N, row, col, k-1);
        }
        dp[cr][cc][k] = prob/8;
        return prob/8;
    }
    
}

先走2步，再走一步正交，稍微快一些，因为在水平垂直的4个方向时已经pass掉一些方向了。

//3ms
class Solution {
    Double[][][] dp;
    public double knightProbability(int N, int K, int r, int c) {   
        dp = new Double[N][N][K+1];
        return dfs(N, r, c, K);
    }
    
    double dfs(int N, int cr, int cc, int k) {
        if(inside(N, cr, cc) == 0) {
            return 0;
        }
        
        if(k <= 0) {
            return 1.0;
        }
        
        if(dp[cr][cc][k] != null) {
            return (double)dp[cr][cc][k];
        }
        
        double prob = 0;
        int[] dirc = new int[]{-2, 0, 2, 0, -2};
        for(int i = 0; i < 4; i++) {
            int row = cr + dirc[i];
            int col = cc + dirc[i+1];
            if(inside(N, row, col) == 0) continue;
            if(dirc[i] == 0) {
                prob += inside(N, row+1, col) * dfs(N, row+1, col, k-1);
                prob += inside(N, row-1, col) * dfs(N, row-1, col, k-1);
            } else if(dirc[i+1] == 0) {
                prob += inside(N, row, col+1) * dfs(N, row, col+1, k-1);
                prob += inside(N, row, col-1) * dfs(N, row, col-1, k-1);
            }
        }
        dp[cr][cc][k] = prob/8;
        return prob/8;
    }
    
    int inside(int N, int cr, int cc) {
        if(cr < 0 || cr >= N || cc < 0 || cc >= N) {
            return 0;
        } else {
            return 1;
        }
    }
}