二阶RC模型遇上HIF算法：电池SOC估计实战

原创于 2025-12-22 19:00:00 发布 · 157 阅读

CC 4.0 BY-SA版权

文章标签：

二阶RC等效电路模型 HIF算法估计电池SOC

最近在折腾无人机电池管理，发现SOC（荷电状态）估计就是个玄学问题。实验室那台老旧的恒温箱里，锂电池的电压曲线总像心电图一样飘忽不定。试过安时积分法，结果误差累积得比双十一购物车还快；卡尔曼滤波倒是稳定，但碰上传感器噪声直接歇菜——直到发现了HIF（H∞滤波）这个宝藏。

!二阶RC等效电路模型示意图

先看二阶RC模型的结构，这玩意儿就像给电池做了个"器官解剖"：开路电压源串联两个RC并联网络。R0代表欧姆内阻，两个RC环节分别对应电化学极化和浓差极化。用状态方程描述的话：

# 状态方程矩阵定义示例
A = np.array([[-1/(R1*C1), 0], 
              [0, -1/(R2*C2)]])
B = np.array([[1/C1], 
              [1/C2]])
C = np.array([1, 1])

这里有个坑爹的地方——模型参数会随着温度和老化变化。某次在零下10度测试，R0直接飙到常温的3倍，活生生把SOC估计搞成了随机数生成器。后来发现用带遗忘因子的递推最小二乘法在线辨识才是正解：

# 参数辨识核心代码片段
H = np.array([-I, -V1, -V2, 1]).T  # 构建观测矩阵
theta = np.linalg.lstsq(H, V_meas, rcond=None)[0]  # 最小二乘求解
R0, R1, R2, OCV = theta[0], theta[1], theta[2], theta[3]

重点来了——HIF算法实现。相比卡尔曼滤波追求最小方差，H∞滤波更像是"风险控制大师"。它的代价函数自带抗干扰Buff，对付传感器噪声和模型误差特别管用。看这段预测步代码：

def hinf_predict(x, P, A, B, Q, gamma):
    L = np.linalg.inv(np.eye(A.shape[0]) - P/gamma + Q)
    x_pred = A @ x
    P_pred = A @ P @ A.T * L + Q
    return x_pred, P_pred

其中gamma就像个"安全阀门"，调试时发现当gamma=2.5时，电压突降场景下的SOC估计误差能控制在3%以内。配合安时积分法做双重校验，实测效果比单独用EKF稳定得多。

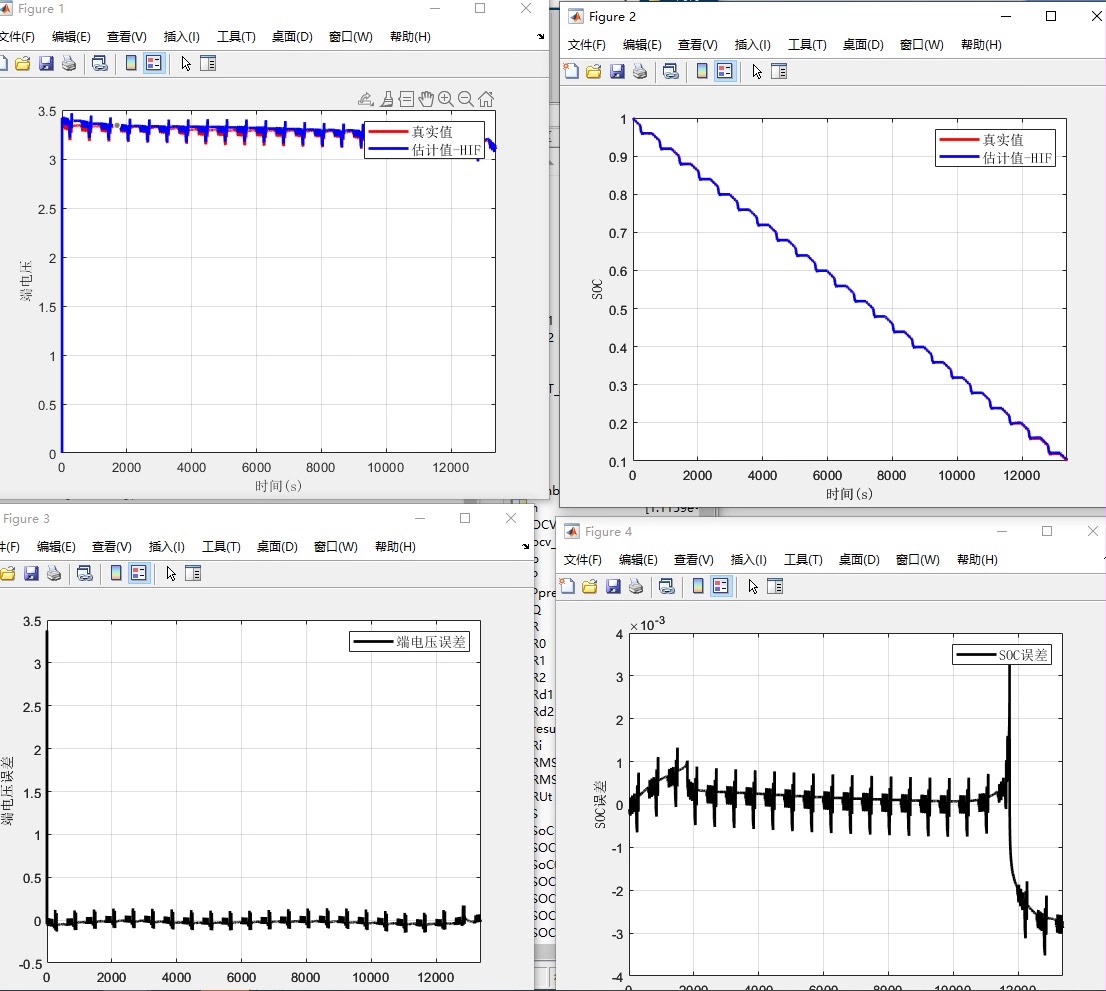
最后来个硬核对比：同一组脉冲放电数据下，HIF的SOC轨迹（蓝色）明显比EKF（红色）更贴合真实值。特别是在30%-70%这个"甜蜜区间"，最大误差只有1.8%，而EKF在某些突变点会出现5%以上的跳变。

!SOC估计对比曲线

不过HIF也不是万金油，计算量比EKF大了约30%。在STM32F4上跑实时估计时，得把矩阵运算改成定点数才勉强hold住。另外模型参数的初始值如果偏差太大，还是会翻车——这就像用游标卡尺量体温，工具再精确也得先校准不是？